2.2. Затухающие электромагнитные колебания

В реальном колебательном контуре кроме индуктивности и емкости имеются потери энергии, которые схематически изображаются включением в колебательный контур активного сопротивления R. При протекании через него электрического тока энергия электромагнитных колебаний переходит в тепловую энергию в результате нагревания элементов цепи, обладающих активным сопротивлением. В связи с этим амплитудное значение тока и напряжения с каждым последующим колебанием уменьшается.

.

После элементарных преобразований этого равенства с учетом выражения (2.7) получим дифференциальное уравнение для реального колебательного контура:

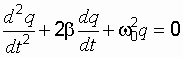.                                                                                                 (2.13)

Здесь приняты обозначения:

,                                                                                                                           (2.14)

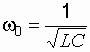.                                                                                                                     (2.15)

Из теории дифференциальных уравнений следует, что в случае, когда b < w ₀ в колебательном контуре возникают затухающие (негармонические) колебания заряда согласно уравнению

,                                                                                                 (2.16)

где b – коэффициент затухания, w – циклическая частота затухающих колебаний находится как

.                                                                                                                 (2.17)

Начальная фаза j ₀ может быть сделанной равной нулю выбором начала отсчета времени.

С учетом формулы (2.6), делением на емкость контура C уравнения (2.16), получим зависимость от времени напряжения на конденсаторе

,                                                                                                     (2.18)

где U₀ = q₀ / C – начальное напряжение на конденсаторе. Это уравнение не является гармоническим, однако может быть записано подобно гармоническому, положив переменную амплитуду колебаний

,                                                                                                                 (2.19)

.                                                                                                         (2.20)

Если b < < w ₀, то циклическая частота затухающих колебаний

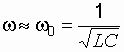, что обычно справедливо для колебательного контура.

Отношение

.                                                                                                            (2.21а)

называется декрементом затухания, а его логарифм

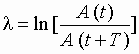                                                                                                          (2.21б)

– логарифмическим декрементом затухания. В (2.21а) и (2.21б) A (t) – амплитуда колебания в момент времени t, а A (t + T) – амплитуда колебания в момент времени t + T, T – период колебания. Декремент затухания показывает, во сколько раз уменьшается амплитуда колебаний за период.

Все характеристики колебательного контура выражаются через параметры колебательного контура R, L и С и взаимосвязаны друг с другом. Так,

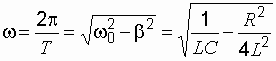,                                                                            (2.22)

.                                                                                                             (2.23)

Качество колебательного контура характеризуется его добротностью, которая показывает во сколько раз запасенная в колебательном контуре энергия больше энергии, теряемой за время t = 2p /T:

.                                                                                                                     (2.24)

Из формулы (2.22) видно, что с увеличением омического сопротивления R частота колебаний уменьшается, а период соответственно возрастает. При  период стремится к бесконечности. При дальнейшем росте сопротивления период становится мнимым, что физически означает прекращение колебаний и переход колебательного контура в апериодический режим. Из формул (2.14), (2.22) и (2.23) следует, что с ростом сопротивления логарифмический декремент затухания будет увеличиваться. При R = 0 электромагнитные колебания в контуре становятся незатухающими.

Энергия в конуре представляет собой сумму энергии электрического поля, запасенной между обкладками конденсатора, и энергии магнитного поля, запасенной в катушке с индуктивностью. Вычислим обе составляющие.

        Сравнивая эти формулы, можно сделать следующие выводы:

1. Полная энергия в контуре остается неизменной: 

2. Частота колебаний энергий в 2 раза превосходит частоту колебаний заряда и тока в контуре.  3. Электрическая и магнитная энергии сдвинуты по фазе на полпериода друг относительно друга; происходит непрерывное перекачивание энергии из одной формы в другую и обратно.