Колебания и волны.

Колебания — повторяющийся в той или иной степени во времени процесс изменения состояний системы около точки равновесия. Например, при колебаниях маятника повторяются отклонения его в ту и другую сторону от вертикального положения; при колебаниях в электрическом колебательном контуре повторяются величина и направление тока, текущего через катушку.

Колебания почти всегда связаны с попеременным превращением энергии одной формы проявления в другую форму.

Характеристики

• Амплитуда— максимальное отклонение колеблющейся величины от некоторого усреднённого её значения для системы, 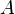  (м)

• Период — промежуток времени, через который повторяются какие-либо показатели состояния системы (система совершает одно полное колебание), 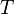  (с)

• Частота — число колебаний в единицу времени, 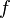  (Гц, с⁻¹).

Период колебаний   и частота   — обратные величины;

 и 

В круговых или циклических процессах вместо характеристики «частота» используется понятие круговая (циклическая) частота   (рад/с, Гц, с⁻¹), показывающая число колебаний за   единиц времени:

• Смещение — отклонение тела от положения равновесия. Обозначение Х, Единица измерения — метр.

• Фаза колебаний — определяет смещение в любой момент времени, то есть определяет состояние колебательной системы.

Гармонические колебания

Гармонические колебания — колебания, при которых физическая (или любая другая) величина изменяется с течением времени по синусоидальному или косинусоидальному закону. Кинематическое уравнение гармонических колебаний имеет вид.

Гармоническими являются колебания,которые происходят под действием силы,пропорциональной смещению колеблящейся точки и направленной противоположно этому смещению.

или

,

где х — смещение (отклонение) колеблющейся точки от положения равновесия в момент времени t; А — амплитуда колебаний, это величина, определяющая максимальное отклонение колеблющейся точки от положения равновесия; ω — циклическая частота, величина, показывающая число полных колебаний происходящих в течение 2π секунд;   — полная фаза колебаний,   — начальная фаза колебаний.

Обобщенное гармоническое колебание в дифференциальном виде

(Любое нетривиальное^[1] решение этого дифференциального уравнения — есть гармоническое колебание с циклической частотой  )

Виды колебаний

• Свободные колебания совершаются под действием внутренних сил системы после того, как система была выведена из положения равновесия. Чтобы свободные колебания были гармоническими, необходимо, чтобы колебательная система была линейной (описывалась линейными уравнениями движения), и в ней отсутствовала диссипация энергии (последняя вызвала бы затухание).

• Вынужденные колебания совершаются под воздействием внешней периодической силы. Чтобы они были гармоническими, достаточно чтобы колебательная система была линейной (описывалась линейными уравнениями движения), а внешняя сила сама менялась со временем как гармоническое колебание (то есть чтобы зависимость от времени этой силы была синусоидальной).

Математический маятник — осциллятор, представляющий собой механическую систему, состоящую из материальной точки, находящейся на невесомой нерастяжимой нити или на невесомом стержне в однородном поле сил тяготения. Период малых собственных колебаний математического маятника длины L неподвижно подвешенного в однородном поле тяжести с ускорением свободного падения g равен

и не зависит от амплитуды колебаний и массы маятника.

Плоский математический маятник со стержнем — система с одной степенью свободы. Если же стержень заменить на растяжимую нить, то это система с двумя степенями свободы со связью. Пример школьной задачи, в которой важен переход от одной к двум степеням свободы.

При малых колебаниях физический маятник колеблется так же, как математический с приведённой длиной.

Уравнение колебаний маятника

Колебания математического маятника описываются обыкновенным дифференциальным уравнением вида

где   ― положительная константа, определяемая исключительно из параметров маятника. Неизвестная функция   ― это угол отклонения маятника в момент   от нижнего положения равновесия, выраженный в радианах;  , где   ― длина подвеса,   ―ускорение свободного падения. Уравнение малых колебаний маятника около нижнего положения равновесия (т. н. гармоническое уравнение) имеет вид:

.

Решения уравнения движения

Гармонические колебания

Маятник, совершающий малые колебания, движется по синусоиде. Поскольку уравнение движения является обыкновенным ДУ второго порядка, для определения закона движения маятника необходимо задать два начальных условия — координату и скорость, из которых определяются две независимых константы:

где   — амплитуда колебаний маятника,   — начальная фаза колебаний,   — циклическая частота, которая определяется из уравнения движения. Движение, совершаемое маятником, называется гармоническими колебаниями.

Физический маятник —осциллятор, представляющий собой твёрдое тело, совершающее колебания в поле каких-либо сил относительно точки, не являющейся центром масс этого тела, или неподвижной оси, перпендикулярной направлению действия сил и не проходящей через центр масс этого тела.