3. Частотный анализ цепи.

Представим формулу коэффициента передачи в операторной форме:

Схема цепи в операторной форме представлена на рисунке 5.

Z1(p)

I(p)

U_Вх(p)

U_Вых(p)

Z2(p)

Рисунок 5 – Схема цепи в операторной форме

Подставляя найденные выражения в формулу коэффициента передачи, получим:

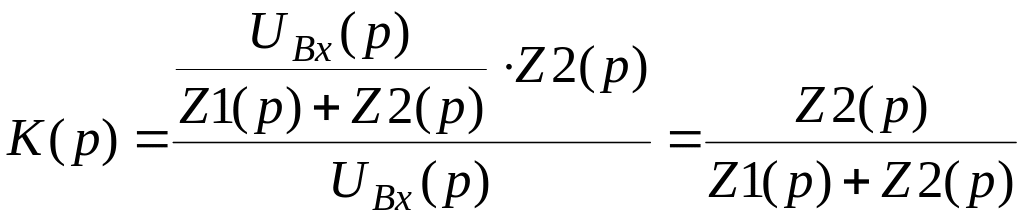
В операторной форме элементы цепи имеют вид:

С учетом этого коэффициент передачи принимает вид:

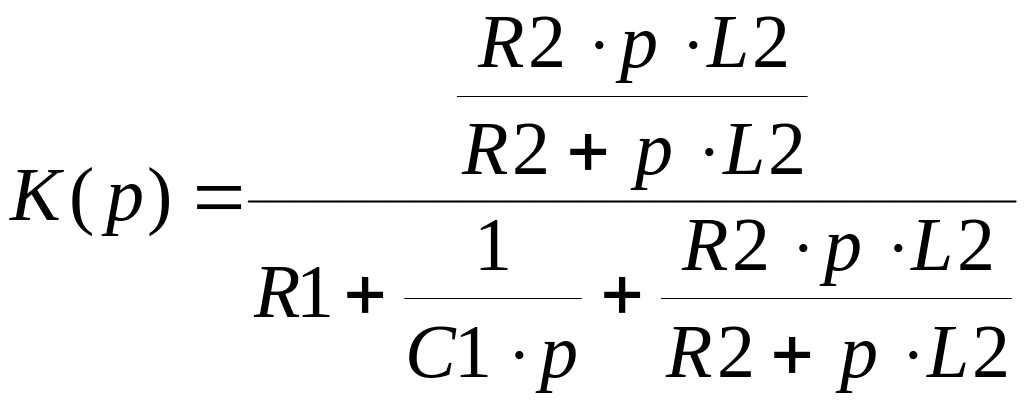
Подставляя в полученную формулу численные значения, получим:

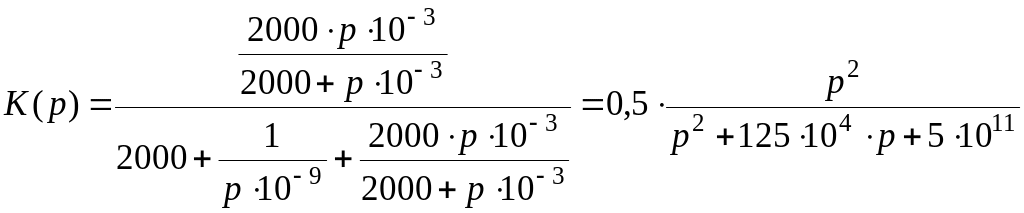
Заменив на , получим частотный коэффициент передач в комплексной форме:

3.1 Амплитудно-частотная характеристика цепи.

График АЧХ приведен на рисунке 5.

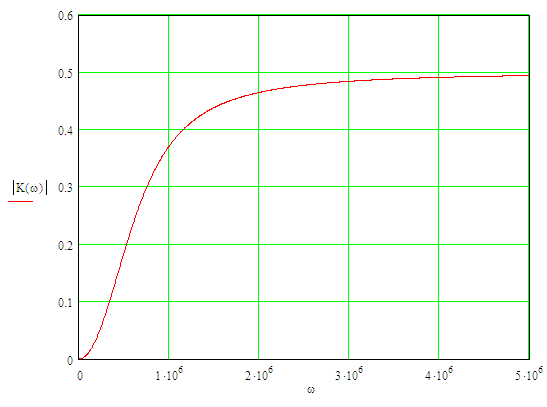
Рисунок 5 – График АЧХ цепи

3.2 Фазо-частотная характеристика цепи.

График ФЧХ представлен на рисунке 6.

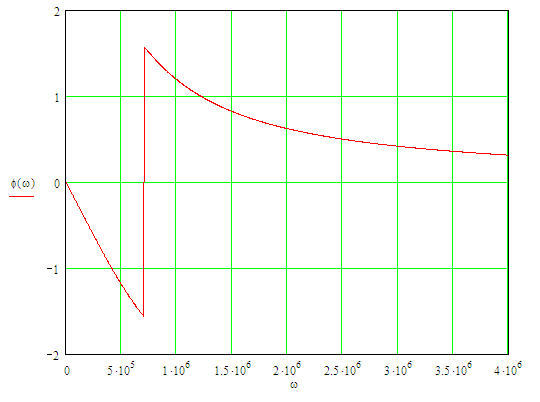
Рисунок 6 – График ФЧХ цепи

4. Импульсная и переходная характеристики цепи.

4.1 Определение переходной характеристики цепи.

Переходная характеристика g(t) представляет собой реакцию цепи на входной сигнал, описываемый единичной функцией .

Представим переходную характеристику g(t) в операторной форме:

Учитывая, что , то переходная характеристика принимает вид:

Подставив значение коэффициента передачи в операторной форме, переходная характеристика принимает вид:

Найдем полюсы функции:

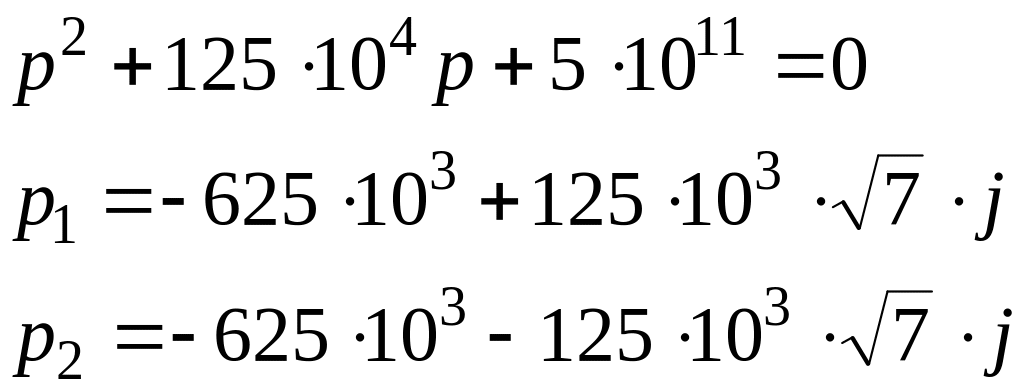
Оригинал находим с помощью теории вычетов:

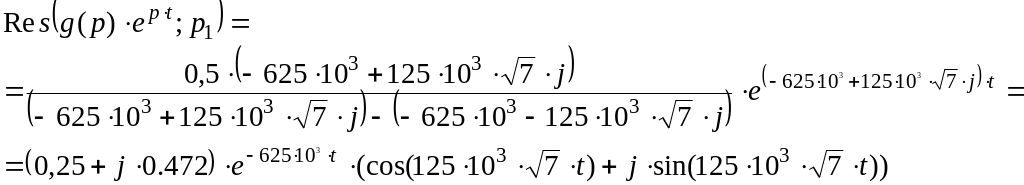
Так как корни и комплексно сопряженные, то для нахождения необходимо взять удвоенную вещественную часть вычета :

График переходного процесса представлен на рисунке 7.

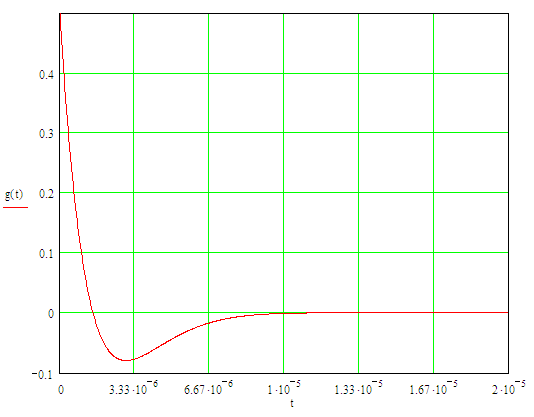
Рисунок 7 – График переходного процесса

4.2 Определение импульсной характеристики цепи.

Импульсной характеристикой цепи является реакция цепи на воздействие входного сигнала, который описывается -функцией.

Так как , то выражение импульсной характеристики можно вычислить:

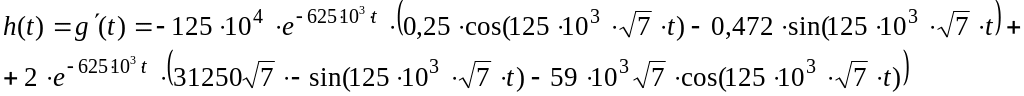
График импульсной характеристики представлен на рисунке 8.

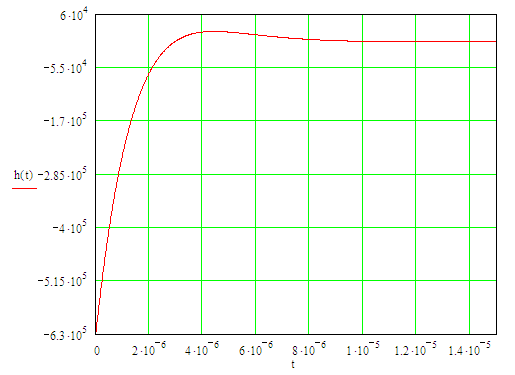
Рисунок 8 – График импульсной характеристики

5. Спектральный анализ выходного сигнала.

5.1 Определение спектральной плотности выходного сигнала.

Спектральная плотность выходного сигнала:

5.2 Нахождение амплитудного и фазового спектров выходного сигнала.

Амплитудный спектр выходного сигнала:

График амплитудного спектра выходного сигнала представлен на рисунке 9.

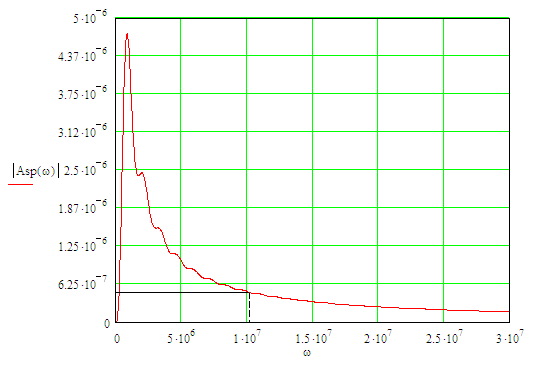
Рисунок 9 – График амплитудного спектра выходного сигнала

Ширина спектра выходного сигнала:

рад/с.

Фазовый спектр выходного сигнала представляет собой аргумент спектральной плотности выходного сигнала:

График фазового спектра выходного сигнала представлен на рисунке 10.

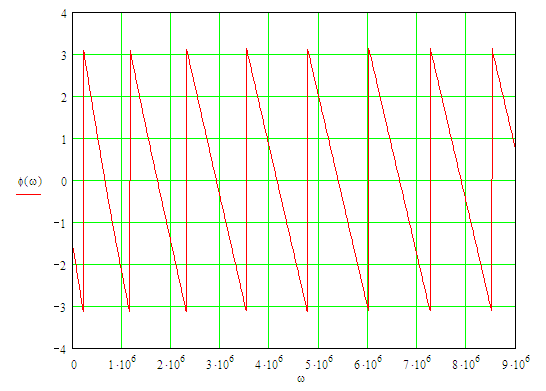
Рисунок 10 – График фазового спектра выходного сигнала

6. Выходной сигнал.

Спектральная плотность выходного сигнала в операторной форме:

Для удобства вычислений разобьем выражение спектральной плотности на две части:

Оригинал будем искать, воспользовавшись теорией вычетов.

Корни характеристического уравнения:

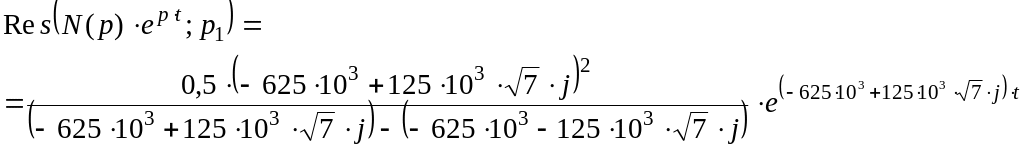
Так как корни и комплексно сопряженные, то для нахождения необходимо взять удвоенную вещественную часть вычета :

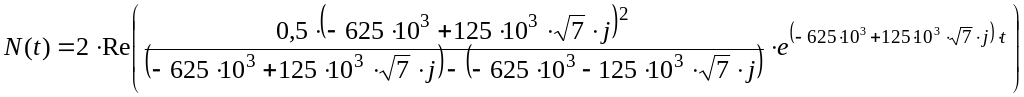
На основе свойства временного сдвига для преобразований Лапласа:

С учетом последних преобразований формула выходного сигнала принимает вид:

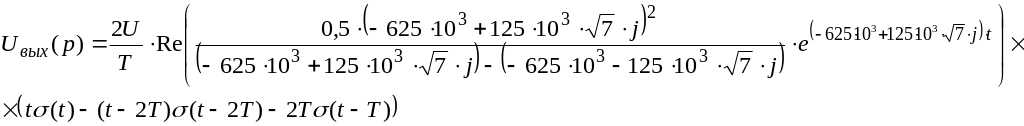
График выходного сигнала представлен на рисунке 11.

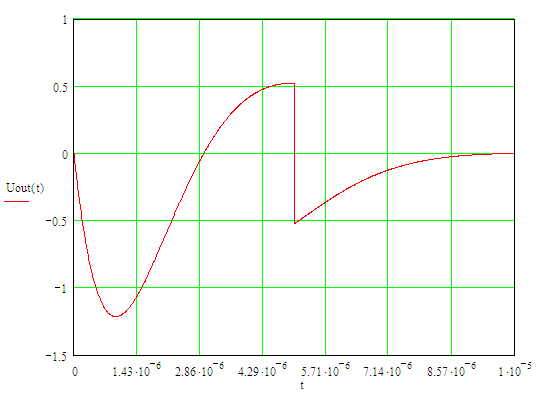
Рисунок 11 – График выходного сигнала