Индивидуальное задание № 1
Рассчитать электрическую цепь со смешанным соединением сопротивления при постоянном входном напряжении (рис.П.1.1).
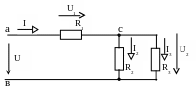
Требуется:
1. Определить токи в ветвях электрической цепи и падения напряжения на ее участках.
2. Составить баланс мощностей электрической цепи.
3. Построить потенциальную диаграмму для контуров цепи.
ВАРИАНТЫ ЗАДАНИЙ
№ вар. |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
|
R1 |
Ом |
1 |
4 |
7 |
10 |
3 |
6 |
10 |
15 |
5 |
8 |
20 |
15 |
11 |
13 |
25 |
R2 |
Ом |
2 |
5 |
8 |
12 |
5 |
8 |
15 |
20 |
10 |
11 |
10 |
5 |
22 |
24 |
20 |
R3 |
Ом |
3 |
6 |
9 |
14 |
7 |
10 |
20 |
25 |
15 |
16 |
30 |
10 |
28 |
32 |
10 |
U |
В |
10 |
|
|
|
|
|
70 |
|
|
|
|
|
55 |
|
|
U1 |
В |
|
5 |
|
|
|
|
|
12 |
|
|
|
|
|
16 |
|
U2 |
В |
|
|
8 |
|
|
|
|
|
20 |
|
|
|
|
|
10 |
I1 |
A |
|
|
|
1 |
|
|
|
|
|
2 |
|
|
|
|
|
I2 |
A |
|
|
|
|
2 |
|
|
|
|
|
3,5 |
|
|
|
|
I3 |
A |
|
|
|
|
|
3 |
|
|
|
|
|
1,5 |
|
|
|
№ вар. |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
25 |
26 |
27 |
28 |
29 |
30 |
|
R1 |
Ом |
1 |
4 |
7 |
10 |
3 |
6 |
10 |
15 |
5 |
8 |
20 |
15 |
11 |
13 |
25 |
R2 |
Ом |
2 |
5 |
8 |
12 |
5 |
8 |
15 |
20 |
10 |
11 |
10 |
5 |
22 |
24 |
20 |
R3 |
Ом |
3 |
6 |
9 |
14 |
7 |
10 |
20 |
25 |
15 |
16 |
30 |
10 |
28 |
32 |
10 |
U |
В |
|
|
|
40 |
|
|
|
|
|
25 |
|
|
|
|
|
U1 |
В |
|
|
|
|
25 |
|
|
|
|
|
18 |
|
|
|
|
U2 |
В |
|
|
|
|
|
30 |
|
|
|
|
|
24 |
|
|
|
I1 |
A |
2 |
|
|
|
|
|
1,8 |
|
|
|
|
|
3 |
|
|
I2 |
A |
|
4 |
|
|
|
|
|
3 |
|
|
|
|
|
,2,5 |
|
I3 |
A |
|
|
2,6 |
|
|
|
|
|
4 |
|
|
|
|
|
2 |
Пример выполнения индивидуального задания № 1
Исходные данные:
U |
R1 |
R2 |
R3 |
В |
Ом |
Ом |
Ом |
30 |
13 |
15 |
10 |
РЕШЕНИЕ:
1. Определение токов I1, I2, I3 и напряжений U1, U2.
Э
квивалентное
сопротивление
Проверка: согласно первому закону Кирхгофа:
I1 = I 2+ I3; 1,58=0,63+0,95; 1,58 =1,58.
Напряжение на сопротивлении R1
U1 = I1R1 = 1,5813 = 20,54 В.
Проверка: согласно второму закону Кирхгофа:
U = U1 + U2; 30 = 20,54 +9,48; 30 =30.
2.
Баланс мощностей
,
где k- номер ветви;
Ik – ток в k-ой ветви;
Rk – сопротивление k-ой ветви;
Ek – алгебраическая сумма;
ЭДС – k-ой ветви;
n- число ветвей в ЭДС;
m – число сопротивлений в электрической цепи.
Так как ЭДС источника питания равна напряжению питания E=U, то
301,58 = 1,58213 + 0,63215 + 0,95210;
47,4 = 32,45 + 5,95 + 9,03;
47,4 Вт 47,43 Вт.
3. Построение потенциальной диаграммы цепи.
Примем потенциал точки «в», равный нулю:
в = 0; тогда а = в + U = 30 В;
с = а – I1R1 = 30 – 1,5813 = 9,46 В;
в = с – I2R2 = 9,46 – 0,6315 = 0.
П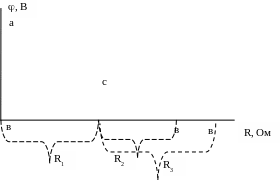
отенциальная
диаграмма строится в координатах
= f(
R
)
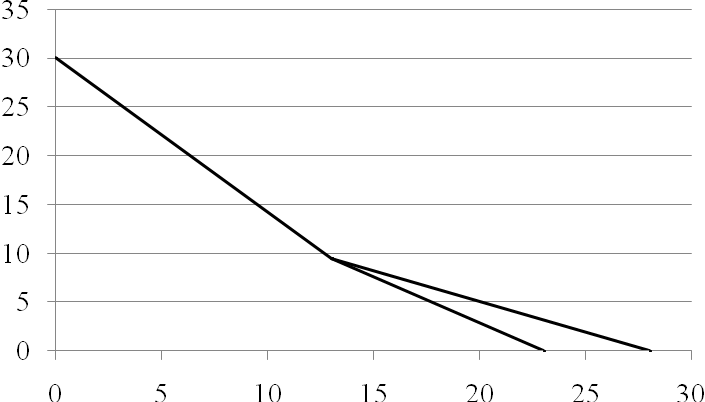
Рис. П.1.2
Индивидуальное задание № 2
Рассчитать токи I1, I2, I3 в электрической цепи (рис.П.2.1) методом наложения (суперпозиции).
З
a
ВАРИАНТЫ ЗАДАНИЙ
Вариант |
Е1 |
Е3 |
R01 |
R03 |
R1 |
R2 |
R3 |
R4 |
R5 |
R6 |
R7 |
схема |
В |
В |
Ом |
Ом |
Ом |
Ом |
Ом |
Ом |
Ом |
Ом |
Ом |
|
|
1 |
90 |
40 |
0,1 |
0,1 |
3,9 |
6 |
4,3 |
10 |
10 |
10 |
10 |
а
|
2 |
100 |
60 |
0,2 |
0,1 |
5,3 |
8 |
3,4 |
12 |
6 |
8 |
12 |
|
3 |
60 |
120 |
0,1 |
0,2 |
4,9 |
5 |
4,8 |
16 |
12 |
16 |
12 |
|
4 |
120 |
70 |
0,1 |
0,1 |
3,4 |
10 |
3,9 |
20 |
20 |
16 |
12 |
|
5 |
110 |
60 |
0,2 |
0,2 |
4,8 |
8 |
2,3 |
24 |
20 |
12 |
16 |
|
6 |
50 |
90 |
0,1 |
0,2 |
2,9 |
6 |
4,8 |
2 |
2 |
1 |
2 |
|
7 |
90 |
30 |
0,3 |
0,2 |
2,7 |
10 |
2,8 |
10 |
10 |
3 |
8 |
|
8 |
140 |
80 |
0,1 |
0,1 |
2,4 |
12 |
2,4 |
12 |
8 |
1,2 |
6 |
б |
9 |
60 |
130 |
0,2 |
0,4 |
3,8 |
5 |
5,6 |
4 |
6 |
2,6 |
5 |
|
10 |
120 |
60 |
0,1 |
0,2 |
3,9 |
10 |
4,8 |
16 |
24 |
2,4 |
12 |
|
11 |
80 |
30 |
0,2 |
0,1 |
2,8 |
4 |
2,3 |
8 |
3 |
5 |
8 |
в |
12 |
160 |
100 |
0,4 |
0,2 |
1,6 |
10 |
4,8 |
12 |
2 |
4 |
12 |
|
13 |
120 |
80 |
0,2 |
0,4 |
2,8 |
8 |
2,6 |
10 |
2 |
3 |
10 |
|
14 |
50 |
100 |
0,4 |
0,2 |
4,6 |
6 |
4,3 |
6 |
2 |
4 |
6 |
|
15 |
70 |
140 |
0,1 |
0,1 |
2,4 |
5 |
2,4 |
24 |
8 |
4 |
24 |
|
16 |
110 |
40 |
0,2 |
0,2 |
2,8 |
4 |
4,8 |
6 |
4 |
5 |
5 |
г |
17 |
90 |
30 |
0,4 |
0,2 |
1,6 |
10 |
2,8 |
12 |
4 |
8 |
8 |
|
18 |
60 |
120 |
0,2 |
0,1 |
2,8 |
8 |
2,4 |
8 |
1 |
7 |
2 |
|
19 |
130 |
70 |
0,4 |
0,4 |
4,6 |
6 |
5,6 |
10 |
2 |
8 |
4 |
|
20 |
50 |
100 |
0,1 |
0,2 |
2,4 |
5 |
4,8 |
6 |
2 |
5 |
3 |
|
21 |
140 |
70 |
0,1 |
0,2 |
3,9 |
6 |
4,3 |
5 |
9 |
9 |
9 |
|
22 |
100 |
160 |
0,2 |
0,1 |
5,3 |
5 |
3,4 |
4 |
12 |
12 |
12 |
|
23 |
110 |
60 |
0,1 |
0,2 |
4,9 |
10 |
4,8 |
5,5 |
4 |
8 |
8 |
д |
24 |
140 |
80 |
0,1 |
0,1 |
3,4 |
8 |
3,9 |
5 |
4 |
2 |
4 |
|
25 |
40 |
90 |
0,2 |
0,2 |
4,8 |
10 |
2,3 |
4 |
2 |
1 |
2 |
|
26 |
90 |
50 |
0,1 |
0,1 |
2,9 |
12 |
2,3 |
4 |
4 |
4 |
4 |
е |
27 |
120 |
60 |
0,3 |
0,2 |
2,7 |
10 |
4,8 |
2 |
12 |
12 |
4 |
|
28 |
100 |
60 |
0,1 |
0,4 |
2,4 |
8 |
2,6 |
3 |
8 |
8 |
1 |
|
29 |
110 |
50 |
0,2 |
0,2 |
3,8 |
10 |
4,3 |
6 |
4 |
4 |
3 |
|
30 |
120 |
70 |
0,1 |
0,1 |
3,9 |
12 |
2,4 |
3 |
6 |
6 |
4 |
Пример выполнения индивидуального задания № 2
Исходные данные:
Е1 |
Е3 |
R0,1 |
R0,3 |
R1 |
R2 |
R3 |
R4 |
R5 |
R6 |
R7 |
В |
В |
Ом |
Ом |
Ом |
Ом |
Ом |
Ом |
Ом |
Ом |
Ом |
200 |
100 |
0,1 |
0,2 |
4 |
6 |
4,8 |
14 |
10 |
10 |
14 |
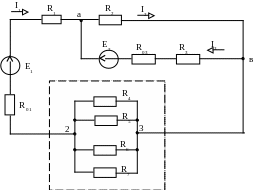
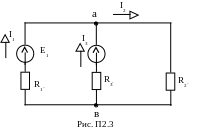Рис. П2.2
РЕШЕНИЕ:
1. Упростим исходную схему электрической цепи (рис.П2.3). Укажем направление токов в ветвях. Определим сопротивления ветвей. Сопротивление первой ветви
R1= R1 + R0,1 + R23;
g23 = 1/R4 + 1/R5 +1/R6 +1/R7= 1/14+1/10+ 1/10 + 1/14 = 0,3429 См ;
R23 = 1/g23 = 2,9 Ом.
R1= 4 + 0,1 + 2,9 = 7 Ом.
Сопротивление второй ветви R2 = R2’= 6 Ом.
Сопротивление третьей ветви
R3 = R3 + R0,3 = 4,8 + 0,2 = 5 Ом.
2
.
Определим частичные токи, созданные
ЭДС Е1
(рис.П2.4)
Э
квивалентное
сопротивление цепи относительно зажимов
ЭДС Е1
Т
ок
в неразветвленной части цепи
Напряжение
между точками а
и в
Токи во второй и третьей ветви
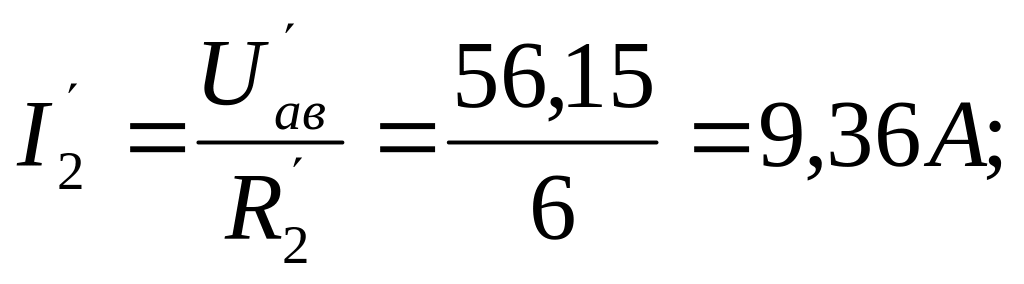
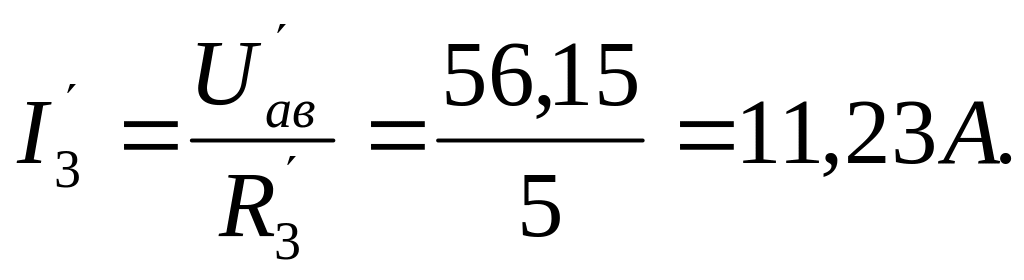
3. Определим аналогично частичные токи, созданные ЭДС Е3 (рис.П2.5):
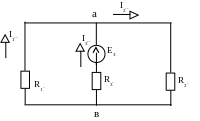
Рис.
П.2.5
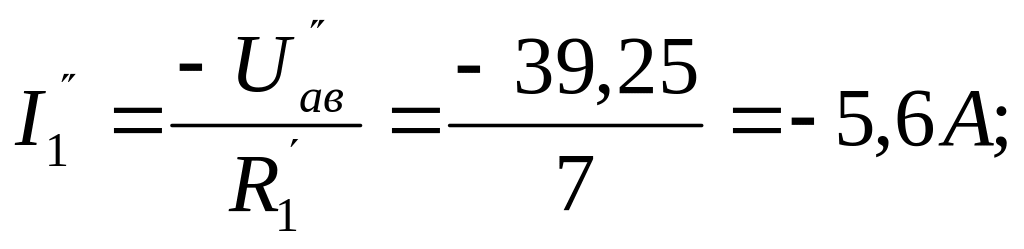
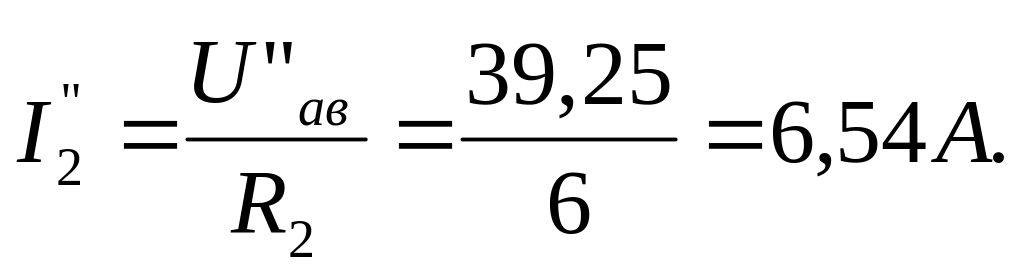
4. Действительные значения токов в ветвях электрической цепи:
I1 = I1 + I1 = 20,65 – 5,6 = 15,05 A;
I2 = I2 + I2= 9,36 + 6,54 = 15,9A;
I3 = I3 – I3 = 12,15 – 11,23 = 0,92 A.
5. Проверка: по первому закону Кирхгофа
I1 + I3 - I2 = 0 ;
15,05 + 0,92 – 15,9 = 0,07.
0,07≈0
Расчет верен.