Раздел 3. Основы теории вероятностей и математической статистики

Элементы комбинаторики. Сочетания, размещения, перестановки. Определение вероятности, случайные величины, вероятность случайных событий,, простейшие теоремы о вероятностях, простейшие характеристики законов распределения (математическое ожидание, дисперсия среднее квадратическое отклонение) нормальный закон распределения и его параметры.

Математическая статистика. Понятие о выборочном методе, корреляциях и регрессиях, проверка статистических гипотез.

Раздел 4. Геометрия

Вычисление значений геометрических величин. Формулы для вычисления площадей поверхностей и объемов тел вращения и многогранников.

4. Методические указания по выполнению самостоятельной работы

0. Указания по выполнению самостоятельной работы

Основной формой обучения студента-заочника является самостоятельная работа над учебным материалом, которая состоит из следующих элементов: изучение материала по учебникам, решение задач, самопроверка, выполнение домашней контрольной работы.

Задания к домашней контрольной работе по дисциплине «Математика» представлены в 17 вариантах. Студент обязан выполнить тот вариант работы, который по номеру совпадает с его порядковым номером в журнале.

Перед выполнением контрольного задания следует изучить разделы курса по изданиям, которые рекомендуются.

Для повышения усвоения качества теоретического материала предлагаются вопросы для самоподготовки.

Вниманию студентов предлагается образец выполнения типового варианта контрольной работы, который содержит решенные задачи, пояснения к решению, а так же основные понятия и формулы, используемые для решения задач.

0. Требования к оформлению самостоятельной работы

При оформлении контрольной работы студент обязан выполнить следующие требования:

1. Работа должна выполняться в отдельной тетради (в клетку), на внешней обложке которой должны быть ясно написаны фамилия студента, его инициалы, полный шифр группы. В конце работы следует указать дату сдачи работы и подпись студента.

2. Контрольные задачи следует располагать в порядке номеров, указанных в заданиях. Перед решением каждой задачи надо полностью переписать ее условия.

3. Решение задач следует излагать подробно, делая соответствующие ссылки на вопросы теории с указанием необходимых формул, теорем.

4. Решение задач геометрического содержания должно сопровождаться чертежами, выполненными аккуратно. Объяснения к задачам должны соответствовать обозначениям, приведенным на чертежах.

5.На каждой странице тетради необходимо оставлять поля шириной 3-4см для замечаний преподавателя.

6.Контрольные работы должны выполняться самостоятельно. Не самостоятельно выполненная работа лишает студента возможности проверить степень своей подготовленности по теме. Если преподаватель установит несамостоятельное выполнение работы или решение заданий не своего варианта, то она не будет зачтена.

7.Студент выполняет тот вариант контрольной работы, который совпадает с номером его фамилии в журнале.

5. Решение типового варианта

Задание № 1. Решить систему линейных уравнений тремя способами (метод Крамера, метод Гаусса и матричный метод)

Метод Крамера

Вычисляем определители

Теперь, воспользовавшись формулами Крамера, найдем значения неизвестных:

Ответ:

Матричный метод

Выписываем матрицу системы

Находим обратную матрицу, для чего вычисляем алгебраические дополнения

Записываем обратную матрицу

Для того, чтобы найти неизвестные умножим обратную матрицу на матрицу-столбец свободных членов.

Ответ:

Метод Гаусса

Запишем расширенную матрицу системы и начнем ее преобразование.

Умножим вторую строчку на 2 и сложим с первой строкой. Первая строка остается неизменной, меняется вторая. Затем умножим первую строку на 3, а вторую – на 2. из первой строки вычитаем третью, и результат записываем в третью строку. Получим следующую матрицу.

Из второй строки вычтем первую и запишем следующую матрицу

Умножим третью строку на 5 и из второй строки вычтем первую.

Получили треугольную матрицу. Возвращаемся к уравнениям, используя данную матрицу.

Ответ:

Задание №2.

Дано комплексное число Z. Требуется:

1. Записать число Z в алгебраической и тригонометрической формах

2. Найти все корни уравнения

а) Пусть дано комплексное число

Комплексным называется число вида , где .

Найдем модуль комплексного числа

Представим комплексное число в алгебраической форме . Дл этого раскроем скобки в числителе и избавимся от иррациональности в знаменателе, т.е. умножим на сопряженное число числитель и знаменатель.

Итак, алгебраическая форма комплексного числа записывается .

Для записи тригонометрической формы найдем модуль комплексного числа и значение главного аргумента.

Для нахождение главного аргумента воспользуемся формулой . Таким образом . Из чего следует, что .

Используя формулу тригонометрической записи комплексного числа , запишем число Z в тригонометрической форме:

b) Решим уравнение

Чтобы найти корни из числа Z, воспользуемся формулой

.

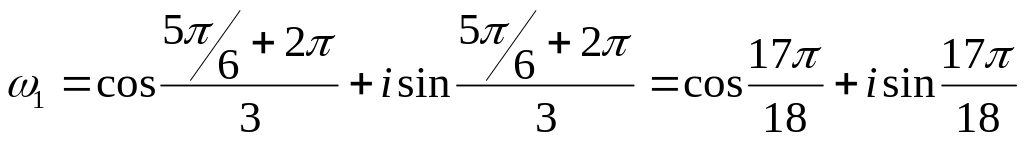
Задание №3.

Исследовать методами дифференциального исчисления функцию и, используя результаты исследования, построить ее график.

Исследование функции можно провести по следующей схеме:

Найти область определения функции.

Исследовать на непрерывность, найти точки разрыва графика функции.

Найти уравнения вертикальных, наклонных асимптот, если они существуют.

Найти интервалы монотонности, точки экстремума функции.

Найти интервалы выпуклости, вогнутости графика функции, точки перегиба.

Выяснить четность, нечетность, периодичность функции.

Найти, если несложно, точки пересечения с осями координат, выяснить поведение функции в бесконечно удаленной точке.

Построить график функции, используя результаты исследования.

Дана функция

Данная функция существует всюду, кроме точки х = 0, т.е. на интервалах . Точка Х=0 является точкой разрыва второго рода, так как

поэтому прямая x = 0 является вертикальной асимптотой.

Наклонная асимптота имеет уравнение , где

Уравнение наклонной асимптоты: . Исследуем функцию на экстремум

Точками экстремума могут быть точки, в которых либо .

Имеем одну критическую точку х =2, так как х =0 не принадлежит области определения функции.

Для удобства составим таблицу:

х		0		2
	+		─	0	+
у				3

Точками перегиба могут быть точки, в которых y′′ = 0 либо y′′ = ∞.

Так как х=0 не принадлежит области определения функции, поэтому точек

перегиба нет

х		0
	+		+
у

Кривая всюду вогнута.

Функция называется четной, если она удовлетворяет равенству f (−x) = f (x) , и

нечетной, если f (−x) = − f (x) . Данная функция не является четной, ни

нечетной. График функции пересекает ось ОХ в точке ( ,0).

3

х

2

Задание №4.

1) Кусок проволоки длиной 48 м сгибают так, чтобы образовался прямоугольник. Какую длину должны иметь стороны прямоугольника, чтобы его площадь была наибольшей.

Решение: Обозначим ширину полученного прямоугольника за х, а длину за у. Тогда . Площадь прямоугольника равна

у

х

Тогда формула для вычисления площади данного прямоугольника будет иметь вид

По правилу о нахождении наибольших и наименьших значений для функции необходимо найти производную и критические точки данной функции.

Ответ: для наибольшей площади прямоугольник должен иметь длины сторон 12 м и 12 м.

2) Число 24 представьте виде суммы двух неотрицательных слагаемых так, чтобы сумма квадратов этих чисел была наименьшей.

Решение: пусть число 24 представимо в виде суммы двух слагаемых . Тогда можем записать: . По условию задачи составляем функцию , исследуем эту функцию на наибольшее и наименьшее значения. По правилу о нахождении наибольших и наименьших значений для функции необходимо найти производную и критические точки данной функции.

Ответ: чтобы сумма квадратов была наименьшей нужно число 24 представить в виде суммы 12 и 12.

Задание №5. Найти площадь плоской фигуры, ограниченной графиком функции и прямыми и осью Ох.

Вначале построим фигуру, ограниченную данными линиями:

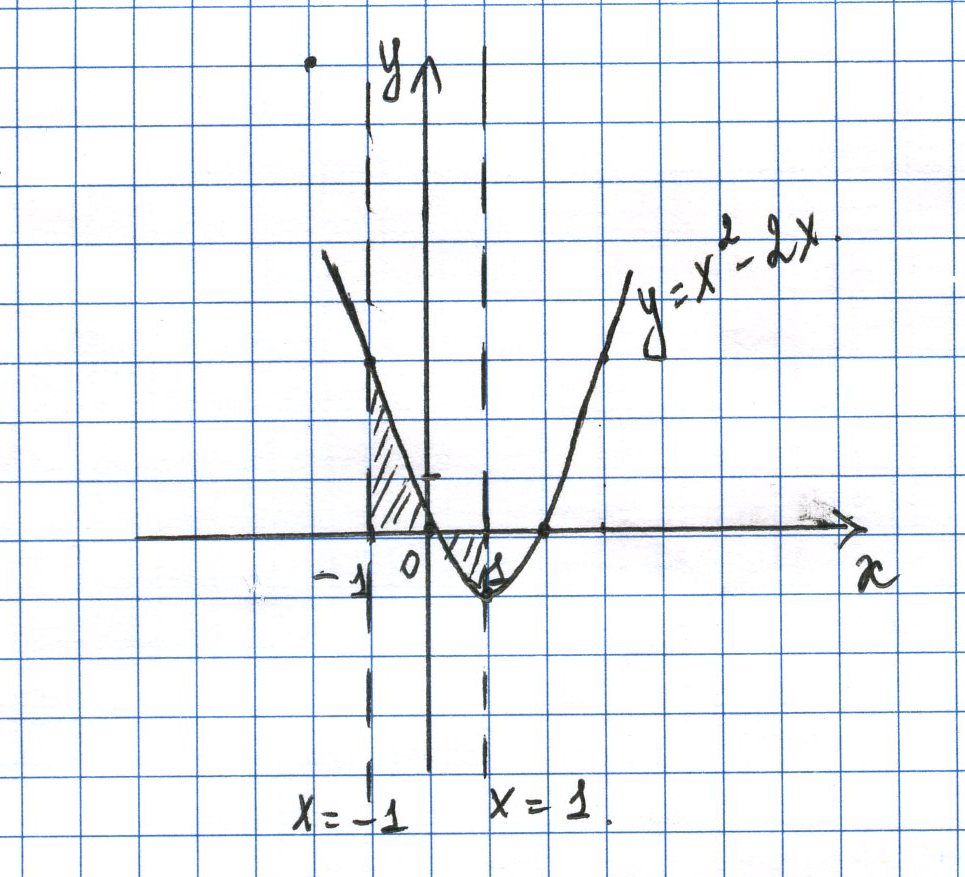
Искомая площадь находится по формуле , следовательно

Ответ: Площадь искомой фигуры 2 (ед²).

Задание №6. Вычислить объем тела, полученного вращением вокруг оси Ох криволинейной трапеции, ограниченной параболами .

Находим точки пересечения парабол, для этого решим уравнение:

Подставив найденные х в одно из уравнений находим ординаты точек М₁ (-1;2) и М₂ (1;2).

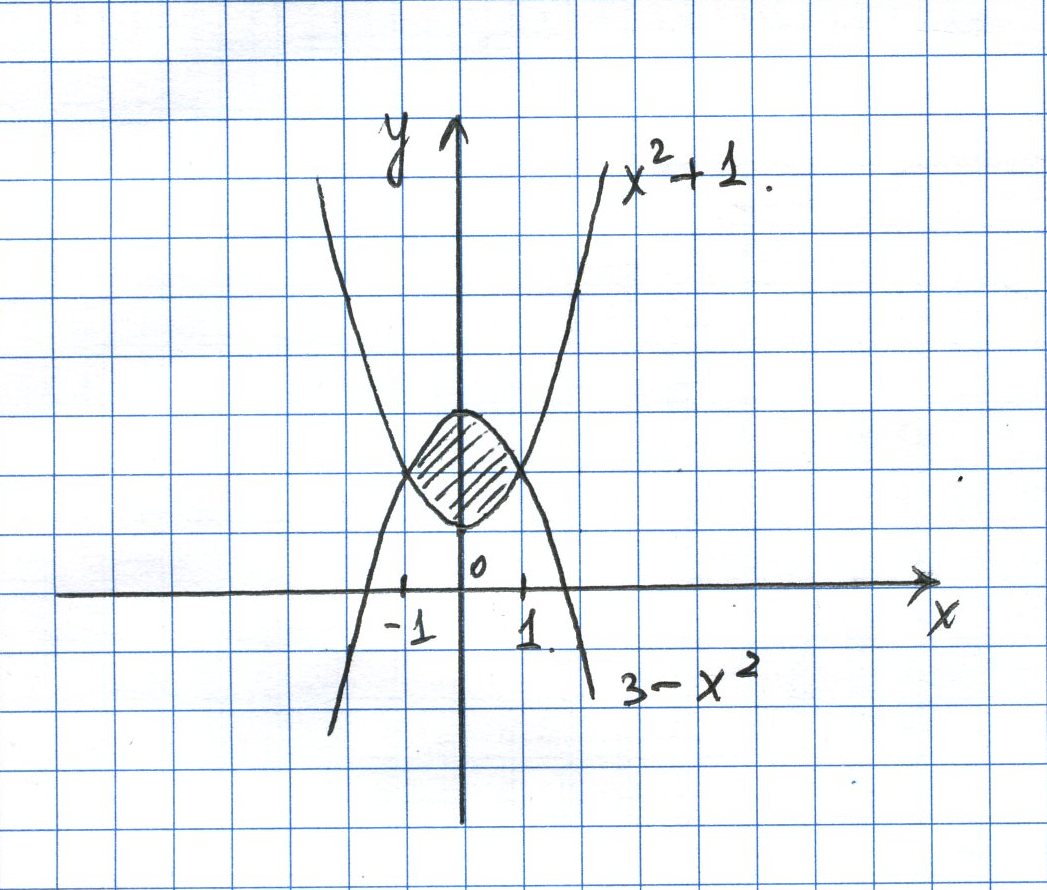
Объем данного тела получаем как разность объемов

Ответ:

Задание №7. Решение задач по теории вероятности с элементами комбинаторики.

№ 7.1. Из колоды в 36 карт вынимаются одна за другой без возвращения 6 карт. Какова вероятность того, что три них будут «черви».

Решение: Событие А – из 6 карт три «черви». Тогда число всевозможных исходов Число исходов, благоприятствующих событию А, равно Таким образом,

Ответ:

№7.4. В коробке лежат 5 синих, 4 красных, 3 зеленых карандаша. Наудачу вынимают 3 карандаша. Найти вероятность того, что это будут карандаши разного цвета.

Решение: Пусть А – все 3 карандаша будут разного цвета. Тогда число всевозможных исходов Число благоприятных исходов Вероятность события А равна

Ответ:

Задание №8.

Вычисление значения геометрических величин

Для вычисления геометрических величин используем формулы:

Площади плоских фигур:

Площадь и объем призмы:

Площадь и объем пирамиды:

Площадь и объем цилиндра:

Площадь и объем конуса:

Задача № 8.1. Найти площадь полной поверхности и объем призмы, в основании которой лежит правильный треугольник со стороной 8 см. и 4 см. Высота призмы 10 см.

Решение: делаем чертеж и записываем дано.

	Дано: - призма, : правильный АВ = 8 см. h = 10 см.
	Найти:

Решение:

Так как в основании лежит правильный треугольник, то находим площадь треугольника по формуле , учитывая, что все стороны равны и все углы в треугольнике равны

Ответ:

Задача № 8.2.

Найти объем тела вращения, полученного вращением прямоугольника со сторонами 12 см. и 16 см., вокруг прямой, проходящей через середины его меньшей стороны.

Решение: Так как меньшая сторона 12 см., то прямая проходит через эту сторону. При вращении получим цилиндр. Высота цилиндра 16 см., а радиус 6 см.

Построим чертеж и запишем дано.

	Дано: АВСД – прям-к ДС = 16 см. СВ = 12 см.
	Найти:

При вращении прямоугольника получается цилиндр. Так как вращение происходит относительно прямой, проведенной через середины меньших сторон, то радиус цилиндра будет равен 6 см.

Ответ: