3. Капиллярные явления. Уравнение Лапласа-Юнга. Уравнение Томсона-Кельвина

Капиллярные явления , физические явления, обусловленные действием поверхностного натяжения на границе раздела несмешивающихся сред. К капиллярным явлениям относят обычно явления жидких сред, вызванные искривлением их поверхности, граничащей с другой жидкостью, газом или собственным паром. Искривление поверхности ведет к появлению в жидкости дополнительного капиллярного давления , величина которого связана со средней кривизной радиуса r поверхности уравнением Лапласа.

Капиллярное давление. Т. к. силы поверхностного (межфазного) натяжения направлены по касательной к пов-сти жидкости, искривление последней ведет к появлению составляющей, направленной внутрь объема жидкости. В результате возникает капиллярное давление, величина к-рого p связана со средним радиусом кривизны пов-сти r₀ ур-нием Лапласа:

p = p₁  p₂ = 2₁₂/r₀, (1)

где p₁ и p₂ - давления в жидкости 1 и соседней фазе 2 (газе или жидкости), ₁₂ - поверхностное (межфазное) натяжение. Если пов-сть жидкости вогнута (r₀<0), давление в ней оказывается пониженным по сравнению с давлением в соседней фазе p₁ < р₂ и p < 0. Для выпуклых пов-стей (r₀ > 0) знак p изменяется на обратный. Отрицат. капиллярное давление, возникающее в случае смачивания жидкостью стенок капилляра, приводит к тому, что жидкость будет всасываться в капилляр до тех пор, пока вес столба жидкости высотой h не уравновесит перепад давления p. В состоянии равновесия высота капиллярного поднятия определяется ф-лой Жюрена:    где _ и ₂ - плотности жидкости 1 и среды 2, g - ускорение силы тяжести, r - радиус капилляра,  - краевой угол смачивания. Для несмачивающих стенки капилляра жидкостей cos  < 0, что приводит к опусканию жидкости в капилляре ниже уровня плоской пов-сти (h < 0). Из выражения (2) следует определение капиллярной постоянной жидкости а = [2₁₂/(₁ — ₂)g]^1/2. Она имеет размерность длины и характеризует линейный размер Z  а, при к-ром становятся существенными К. я. Так, для воды при 20 °С а = 0,38 см. При слабой гравитации (g : 0) значение а возрастает. На участке контакта частиц капиллярная конденсация приводит к стягиванию частиц под действием пониж. давления p < 0.  Уравнение Кельвина. Искривление пов-сти жидкости приводит к изменению над ней равновесного давления пара р по сравнению с давлением насыщ. пара p_s над плоской пов-стью при той же т-ре Т. Эти изменения описываются ур-нием Кельвина:    где   - молярный объем жидкости, R - газовая постоянная. Понижение или повышение давления пара зависит от знака кривизны пов-сти: над выпуклыми пов-стями (r₀ > 0) p > p_s; над вогнутыми (r₀ < 0) р < р_s.Так, над каплями давление пара повышено; в пузырьках, наоборот, понижено. На основании ур-ния Кельвина рассчитывают заполнение капилляров или пористых тел при капиллярной конденсации. Т. к. значения р различны для частиц разных размеров или для участков пов-сти, имеющей впадины и выступы, ур-ние (3) определяет и направление переноса в-ва в процессе перехода системы к состоянию равновесия. Это приводит, в частности, к тому, что относительно крупные капли или частицы растут за счет испарения (растворения) более мелких, а неровности пов-сти некристаллич. тела сглаживаются за счет растворения выступов и залечивания впадин. Заметные различия давления пара и р-римости имеют место лишь при достаточно малых r₀ (для воды, напр., при r₀  0,1 мкм). Поэтому ур-ние Кельвина часто используется для характеристики состояния коллоидных систем и пористых тел и процессов в них. 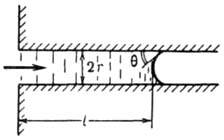   Рис. 2. Перемещение жидкости на длину l в капилляре радиуса r;  краевой угол.

2.3.1. Уравнение Томсона (Кельвина). Из выражения 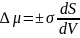следует, что в

фазе, имеющей выпуклую поверхность раздела, вещество имеет больший

химический потенциал, чем под плоской поверхностью, а под вогнутой поверхностью – меньший. Чтобы капля жидкости находилась в равновесии с окружающим паром, давление пара (pr) над каплей с радиусом r должно быть выше, чем давление пара (р0) над плоской поверхностью. Считая пар идеальным газом, связь между химическим потенциалом и давлением пара над каплей можно представить выражением: =

Для плоской поверхности :

= 1.

Подставим значения и μ в уравнение 1. :

откуда

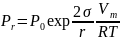
Полученное у р а в н е н и е Т о м с о н а (К е л ь в и н а) справедливо

для тел со сферической выпуклой поверхностью (капля, мениск несмачивающей жидкости в капилляре и т.д.). Согласно этому уравнению давление

насыщенного пара над каплей будет тем больше, чем выше поверхностное

натяжение жидкости и меньше радиус капли. Например, для капли воды с

радиусом 100 нм расчет дает pr /р0 = 1,01, т.е. Давление пара увеличивается на

1 %, а при радиусе 10 нм это увеличение уже составляет 11 %.

В общем случае для тел произвольной формы и с учетом знака кривизны поверхности уравнение Томсона (Кельвина) имеет вид: где знак плюс относится к выпуклым поверхностям, а минус – к вогнутым

Билет № 11