Уравнения Максвелла. Использование уравнений Максвелла для вывода различных термодинамических соотношений.
Уравнения Максвелла.
-1 уравнение Максвелла
-2-е уравнение Максвелла
– 3-е уравнение Максвелла
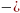– 4-е
уравнение Максвела
Все 4 уравнения Максвелла представляют собой частные производные энтропии по давлению (отрицательные значения) или частные производные Энтропии по объему (положительные ). Данные уравнения очень полезны в термодинамических расчетов.
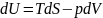
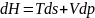
Разделим данные выражения на dv, dp, соответственно при t=const.
(
Применим 3,4 уравнение Максвелла:
Получим
уравнения связывающие объем, температуру
и давление. Поскольку для 1 моля газа
p=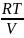
,
то
Отсюда имеем: (
2. Разделение веществ путем перегонки. Азеотропные смеси и их свойства. Правила Вревского
2.1 Перегонка
Перегонка- процесс разделения жидкой смеси и последующей конденсации паров (перехода их в жидкое состояние).Разделение путем перегонки основано на различной температуре кипения отдельных веществ входящих в состав смеси. Так, если смесь состоит из двух компонентов, то при испарении компонента с более низкой температурой кипения (низко-копящий компонент) переходить в пары, а компонент с более высокой температурой кипения (высоко-кипящий компонент )остается в жидком состоянии. Полученные пары конденсируется , образуя дистиллят или ректификат , а не испарённая жидкость называется остатком.
2.2. Азеотропные Смеси , жидкие смеси, характеризующиеся равенством составов равновесных жидкой и паровой фаз. При их перегонке образуется конденсат того же состава, что и исходный р-р; поэтому азеотропные смеси наз. также нераздельнокипящими. Наличие азеотропных смесей существенно затрудняет разделение жидких смесей и требует применения специальных методов ректификации.
2.3. Законы Вревского описывают зависимость состава равновесных жидкой и паровой фаз двойных систем от температуры (давления).
Основываются на общих термодинамических соотношениях, устанавливающих условия равновесия в двухфазных системах, частным случаем которых является равновесие жидкость — пар. При выводе законов Вревского сделан ряд допущений, в частности предполагается, что поведение газовой фазы близко к поведению идеального газа. Поэтому законы Вревского справедливы только для области температур и давлений, значительно удалённой от критической точки равновесия жидкость — пар в данной системе.
Первый закон Вревского
При данном составе жидкой фазы равновесная с ней газовая фаза с увеличением температуры (давления) обогащается тем компонентом, для которого больше парциальная мольная теплота испарения. Приближенно вместо парциальной мольной теплоты испарения данного компонента можно использовать теплоту испарения чистого вещества.
Второй закон Вревского
В азеотропной смеси с максимумом на изотерме зависимости общего давления от состава (минимумом на изобаре температур кипения) при повышении температуры (давления) возрастает концентрация компонента с большей парциальной мольной теплотой испарения. В азеотропной смеси с минимумом общего давления (максимумом температуры кипения) при повышении температуры (давления) возрастает концентрация компонента с меньшей парциальной мольной теплотой испарения. Этот закон особенно важен при разработке процессов азеотропной ректификации.
Третий закон Вревского
При изменении температуры в системах, для которых на кривой зависимости общего давления от состава имеется максимум (на кривой температур кипения — минимум), состав пара, находящегося в равновесии с раствором постоянного состава, и состав азеотропной смеси изменяются в одном направлении; если же кривая общего давления имеет минимум (кривая температур кипения — максимум), то при изменении температуры состав пара, находящегося в равновесии с раствором постоянного состава, и состав азеотропной смеси изменяются в противоположных направлениях.