2. Парциальные мольные величины и их определение из опытных данных для бинарных систем. Уравнения Гиббса-Дюгема.

Для однородной функции первой степени выполняется теорема Эйлера: Z=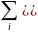 В соответствии с ней, внутренняя энергия, энтальпия, энергии Гельмгольца и Гиббса могут быть записаны в виде:

А) U=

Б) G=

В) F=

Г) H=

Частные производные термодинамических функций (Z) по количеству i-го компонента при фиксированных давлении, температуре и количествах остальных компонентов получили название парциальных мольных величин.

Z= , где Z – любое экстенсивное свойство (U, H, F. G, S, V, Cp, …) , Zi – соответствующая ему парциальная мольная величина. Парциальные мольные свойства компонентов гомогенной смеси – интенсивные свойства, зависящие от температуры, давления и концентраций других компонентов. Они являются взаимозависимыми функциями, связь между ними легко установить, если сравнить полные дифференциалы исходной функции Z(T,p, n) и Z .

+ ,

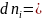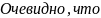
– это уравнение получило название Уравнение Гиббса-Дюгема. Если принять, что Z = G , и учесть, что парциальная энергия Гиббса совпадает с химическим потенциалом:

то можно записать уравнение Гиббса-Дюгема в наиболее распространенной форме:

При p,T = const, это уравнение переходит в 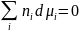. Уравнение Гиббса-Дюгема позволяет по известной функциональной зависимости парциальной мольной величины одного компонента рассчитывать парциальные величины других компонентов, и далее интегральные свойства фазы.

1. Определение парциальных мольных величин из опытных данных для бинарных систем.

• Аналитические

– дифференцирование аналитической зависимости интегрального свойства от остава раствора по количеству молей компонентов.

– интегрирование уравнения Гиббса-Дюгема

Если известна экспериментальная зависимость парциального свойства от

состава для одного компонента, то для второго ее можно получить

интегрированием уравнения .Например, для бинарного раствора:

• Графические

Для двухкомпонентной системы парциальные мольные свойства компонентов можно найти методом пересечений (отрезков). Строится график зависимости изучаемого свойства раствора, отнесенное к одному молю , от мольной доли х2.

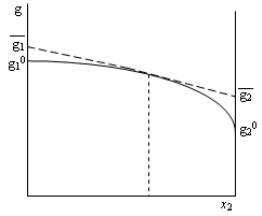
Затем при данном составе проводится касательная в точке, отвечающей

конкретному составу смеси. Пересечение касательной с осями ординат в

точках х2=0 и х2=1 дает значения парциальных мольных величин первого и

второго компонента, соответственно.

3. Расчеты констант равновесия химических реакций с использованием таблиц стандартных значений термодинамических функций.

Для определения изменения энергия Гиббса, сопровождающего химическую реакцию, по уравнению

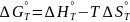
Кроме теплового эффекта реакции необходима величина 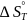,являющаяся разностью абсолютных значений энтропии продуктов реакции и исходных веществ.

Абсолютные значения энтропии могут быть вычислены на основе третьего принципа термодинамики для любой температуры их теплоемкости и теплот фазовых переходов.

Для расчета равновесий достаточно располагать стандартными значениями энтропии взаимодействующих веществ при одной температуре, например Е=298К. Тогда определится из уравнения , в котором сумма двух первых членов равна , а сумма двух последних равна

Расчеты по этому уравнению значительно упрощаются , если воспользоваться методом Темкина и Шварцмана, преобразовавшими уравнение в следующее:

.

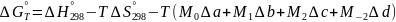В этом уравнение коэффициенты М не зависят от природы реагирующих веществ, а зависят только от температуры и могут быть найдены в таблицах.

После того как определено константа равновесия вычисляется по уравнению

lg

на основании тепловой теоремы Нернста константа равновесия для газовых реакций и для гетерогенных реакций, в которых участвуют газы, может быть вычислена по уравнению

lg

где – разность истинных химических постоянных продуктов реакции и исходных веществ.

Истинные химические постоянные могут быть вычислены по уравнению Клапейрона-Клаузиуса, и для большого числа газообразных веществ они табулированы.

Нернстом предложены, кроме того, следующие приближенные уравнения для вычисления константы равновесия :

lg и lg (2.)

Где - разность условных химических постоянных продуктов реакции и исходных веществ, 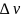–ь разность между числом молей конечных и исходных газообразных веществ. Значения i также табулированы. При расчетах по уравнению (2.)для двухатомных, кроме водорода и многоатомных газов i может быть принято равным 3, а для водорода и одноатомных газов – равным 1,5; вычисляется из эмпирического уравнения Нернста:

Как видно из этого последнего уравнения для вычисления , которое не зависит от температуры, нужно располагать значения теплоемкостей реагирующих веществ при одной температуре.

Ответ на БИЛЕТ 7