2. Химический потенциал идеального газа и неидеальных газов. Метод летучести Льюиса. Различные методы вычисления летучести из опытных данных.

µ0- это хим. Потенциал при стандартных условиях, зависит от природы газа и температуры.

2.. Если давление изменяется от р1 до р2 то

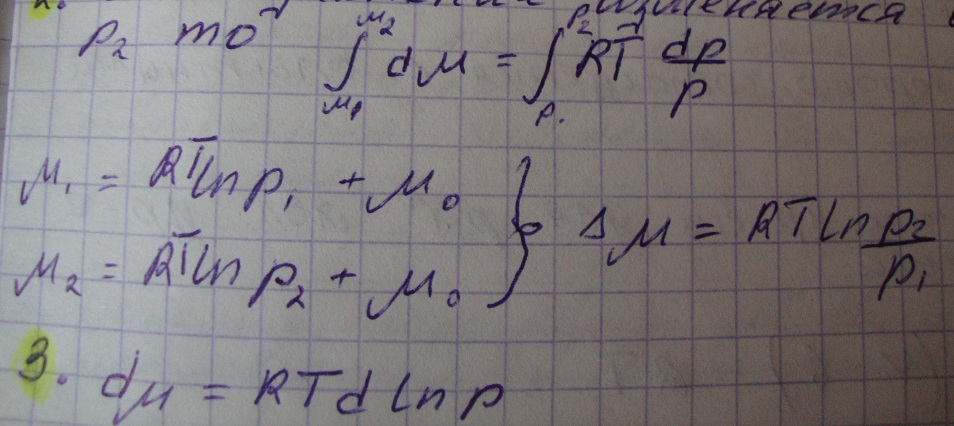
Реальные газы

Для реального газа наиболее удовлетворительные результаты по расчету дает уравнение Питти-Бриджмена

Где это поправка на давление

b- поправка на объем.

Чтобы упростить расчет для реальных газов было введено понятие летучесть (футивность) – это некая функция давления, подстановка которой в уравнение справедливое для идеальных газов позволяет использовать их для реальных

Коэф. Летучести – f=j*p

Т.е. для µ реального газа

µ=µ^*+ RTlnf

3. Зависимость констант равновесия от температур. Уравнение изохоры и изобары реакции. Их термодинамический вывод.

Билет №13

1. Зависимость константы равновесия от температуры. Уравнения изо­бары и изохоры реакции, их термодинамический вывод.

Зависимость константы равновесия от температуры.

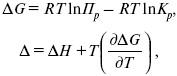
Уравнения изо­бары и изохоры реакции, их термодинамический вывод.

Уравнение изобары:

Уравнение изохоры:

По ним судят о направлении протекания реакции:

2. Мольные и парциальные мольные величины. Уравнение Гиббса – Дюгема.

Большинство свойств, поддающихся количественному выражению, может быть разделено на две группы: экстенсивные и интенсивные. Экстенсивные свойства пропорциональны количеству вещества (объем, масса, внутренняя энергия, энтропия). Интенсивные свойства, как температура и давление, не зависят от количества вещества.

парциальный объем:

парциальная энергия Гиббса:

ГИББСА - ДЮГЕМА УРАВНЕНИЕ - термодинамич. соотношение между приращениями темп-ры T, давления P и хим. потенциалов многокомпонентной термодинамич. системы:

где S - энтропия, V - объём, Ni - число частиц i-го компонента. Для многофазной системы i учитывает также разл. фазы.

Получено Дж. У. Гиббсом в 1875 и широко применялось П. Дюгемом (Дюэмом) (P. Duhem). Г. - Д. у. устанавливает связь между интенсивными термодинамич. параметрами, к-рые при термодинамич. равновесии постоянны. Оно следует из того, что, согласно второму началу термодинамики, приращение Гиббса энергии G равно

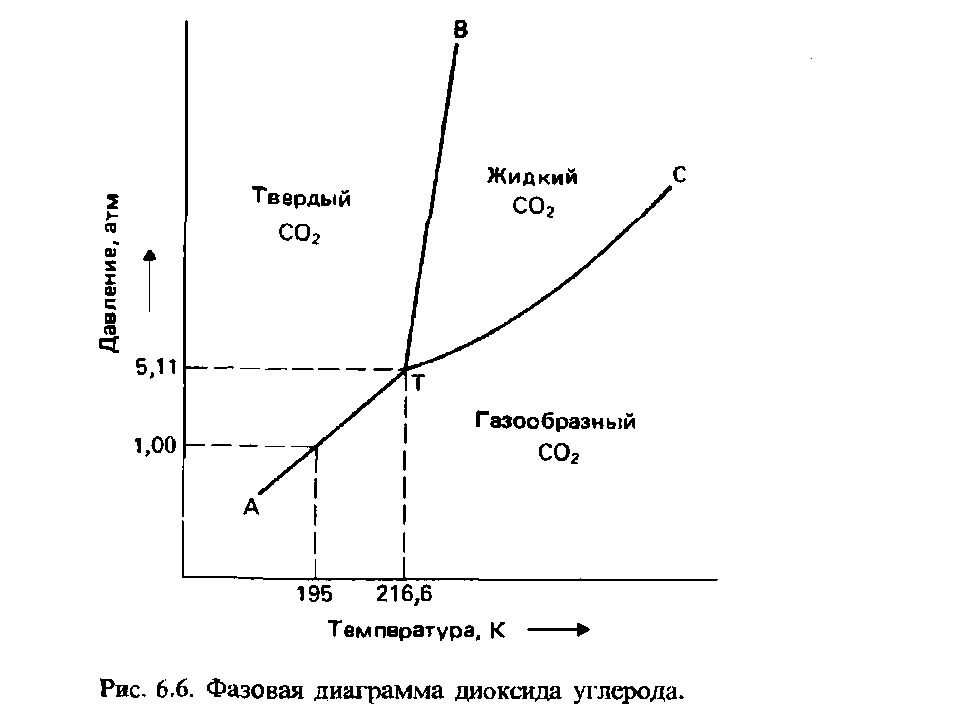
3. Однокомпонентные системы. Диаграммы состояния воды, серы, фосфора и углерода.

Однокомпонентной системой является любое простое в-во или хим. соед., обладающее строго определенным составом в газообразном, жидком и твердом состояниях. Диаграммы состояния обычно строят на плоскости в координатах Т-р (рис. 1). Фазовые поля (области существования) пара V, жидкости L и твердой фазы S дивариантны, т.е. допускают одновременное изменение двух параметров состояния - Т и Р.

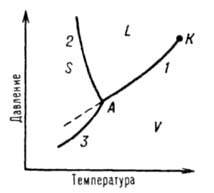
ДИАГРАММА ВОДЫ:

Области фазовой диаграммы, ограниченные кривыми, соответствуют тем условиям (температурам и давлениям), при которых устойчива только одна фаза вещества.

ДИАГРАММА УГЛЕРОДА:

диаграмма серы:

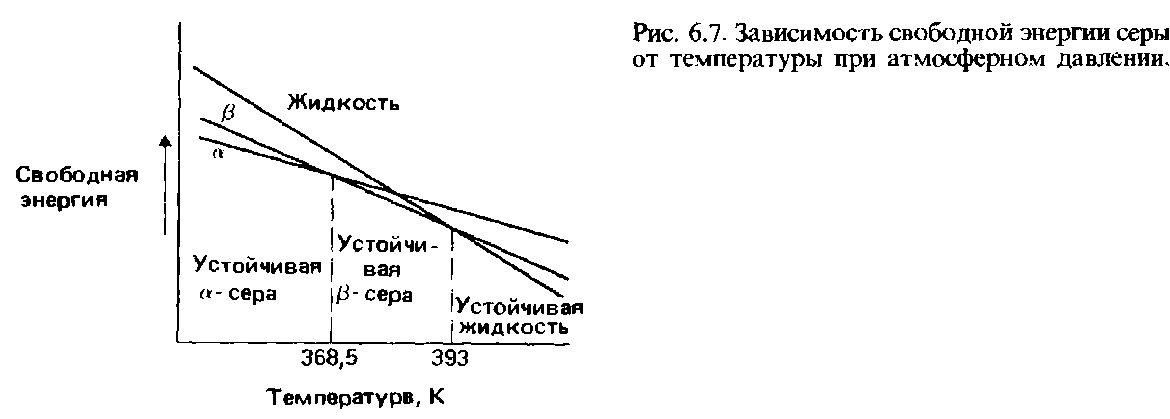
диаграмма фосфора:

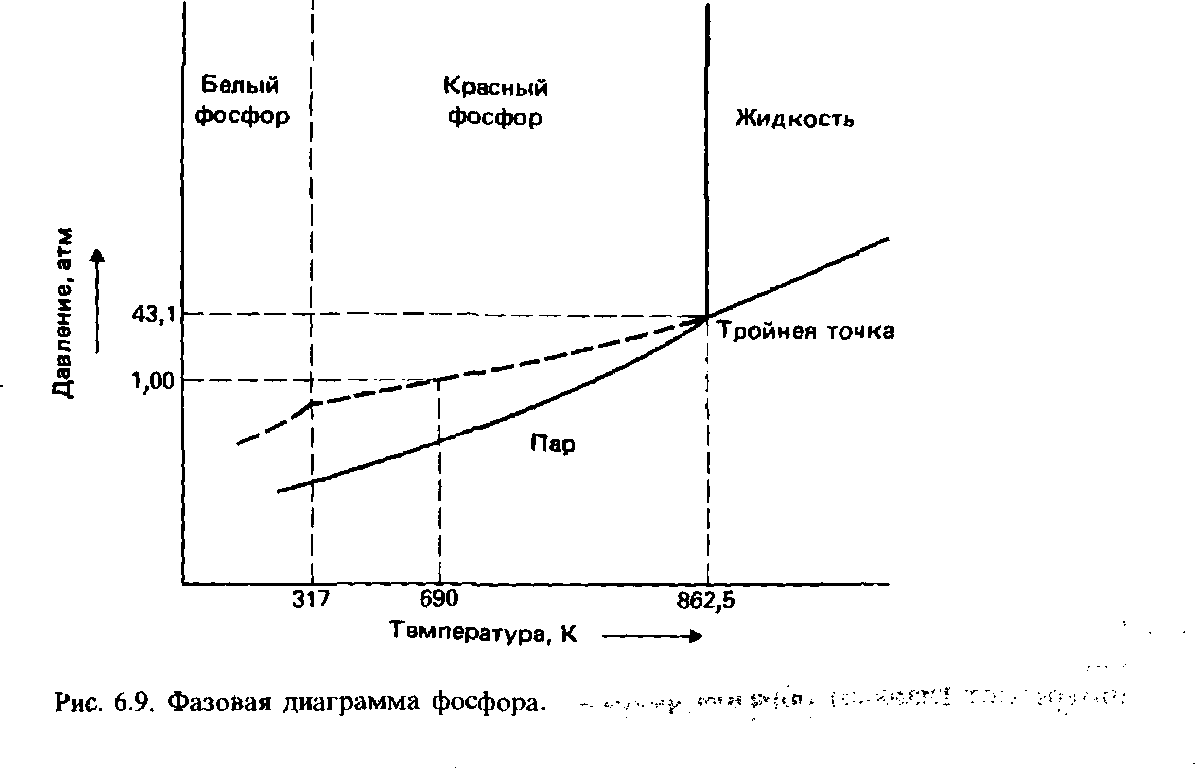
Экзаменационный билет № 14

1. Уравнение Гиббса - Гельмгольца и его роль в химии. Работа и теп­лота химического процесса. Химические потенциалы, их определение, вы­числение и свойства. Равновесие в поле внешних сил. Полные потенциалы.

Уравнение Гиббса – Гельмгольца - термо-динамич. соотношения, устанавливающие связь между внутренней энергией U и Гелъмголъца энергией (свободной энергией) F или между энтальпией H и Гиббса энергией (свободной энтальпией) G:

Теплота Q и работа A функциями состояния не являются, ибо они служат формами передачи энергии и связаны с процессом, а не с состоянием системы.

А = р ∆V, Где ∆V — изменение объема системы (V2 – V1).

Qp = ∆U + p∆V,

Qp= (U2 – U1) + p(V2 – V1)

Qp = (U2 + pV2) – (U1 + pV1)

Сумму U+ pV обозначим через Н, тогда

Qp = H2 – H1 = ∆H

Хими́ческий потенциа́л — термодинамическая функция, применяемая при описании состояния систем с переменным числом частиц. Определяет изменение термодинамических потенциалов (энергии Гиббса, внутренней энергии, энтальпии и т. д.) при изменении числа частиц в системе. Определение химического потенциала можно записать в виде:

Для систем, состоящих из одного компонента, можно доказать, что химический потенциал задаётся формулой:

Полные дифференциалы термодинамических потенциалов имеют вид:

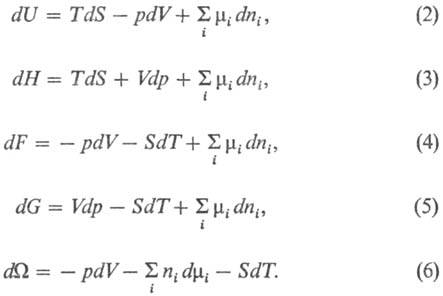
2. Поверхностное натяжение. Правило Юнга.

ПОВЕРХНОСТНОЕ НАТЯЖЕНИЕ, стремление в-ва (жидкости или твердой фазы) уменьшить избыток своей потенциальной энергии на границе раздела с др. фазой (поверхностную энергию). Определяется как работа, затрачиваемая на создание единицы площади пов-сти раздела фаз (размерность Дж/м2).

Поверхностное натяжение зависит от температуры. Для многих однокомпонентных неассоциированных жидкостей (вода, расплавы солей, жидкие металлы) вдали от критической температуры хорошо выполняется линейная зависимость:

Юнг рассматривал величины поверхностного натяжения как векторы сил, стремящихся сократить избыточную поверхностную энергию системы:

s_тп = s_тж + s_жпCos q (правило Юнга)

3. Различные виды констант равновесия и связь между ними. Химиче­ская переменная. Химическое равновесие в идеальных и неидеальных систе­мах. Термодинамический вывод закона действия масс.

Состояние равновесия в химической термодинамике характеризуется особой величиной — константой равновесия Kравн. Константа равновесия может быть выражена через различные параметры системы, что отражается индексами: KC (через молярные концентрации), KX (через мольные доли), KP (через парциальные давления) и др.

Константы равновесия различных типов связаны друг с другом следующим образом:

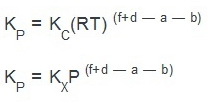
Параметр λ называют химической переменной или пробегом реакции, величина которого зависит от величины числа моль веществ и величины стехиометрического коэффициента. Так, если в химической смеси веществ одновременно может протекать несколько химических реакций, то каждая из них будет характеризоваться своей химической переменной, то есть λ1, λ2, λ3 и т. д.

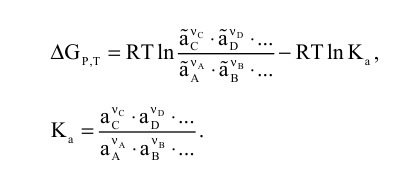
Экзаменационный билет № 15

1. Теплота сгорания. Теплоты образования. Зависимость теплового эф­фекта реакции от температуры (уравнение Кирхгоффа). Зависимость тепло­емкости от температуры и расчеты тепловых эффектов реакций.

Теплота́ сгора́ния — это количество выделившейся теплоты при полном сгорании массовой (для твердых и жидких веществ) или объёмной (для газообразных) единицы вещества. Измеряется в джоулях или калориях. Теплота сгорания, отнесённая к единице массы или объёма топлива, называется удельной теплотой сгорания (дж или кал на 1 кг, м³ или моль). Высшая теплота сгорания - то количество теплоты, которое выделяется при полном сгорании вещества, включая теплоту конденсации водяных паров при охлаждении продуктов сгорания. Низшая теплота сгорания соответствует тому количеству теплоты, которое выделяется при полном сгорании, без учёта теплоты конденсации водяного пара.

Низшая и высшая теплота сгорания связаны соотношением:

: (для твердого вещества)

: (для жидкого вещества)

Принято использовать теплоты образования соединений из чистых элементов в стандартных условиях:

1. Для твердых, жидких и газообразных веществ стандартное состояние определяется как наиболее распространенная форма элемента при 25 оС (298 К) и давлении 1 атмосфера (1 атм).

2. Теплота образования чистых элементов по определению равна нулю.

Тепловой эффект химической реакции или изменение энтальпии системы вследствие протекания химической реакции — отнесенное к изменению химической переменной количество теплоты, полученное системой, в которой прошла химическая реакция и продукты реакции приняли температуру реагентов.

Изменение энтальпии реакции при увеличении температуры от Т1 до Т2 рассчитывают по закону Кирхгофа:

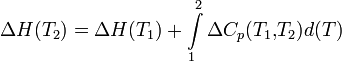
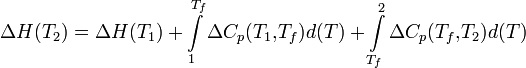
Теплоёмкостью называется количество тепла, которое необходимо подвести к единице массы вещества, чтобы повысить его температуру на один градус. В зависимости от единицы массы вещества различают удельную и молярную теплоёмкость.

Теплоёмкость при постоянном объёме СV=

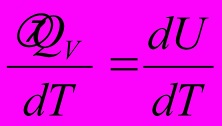
Теплоёмкость при постоянном давлении СР =

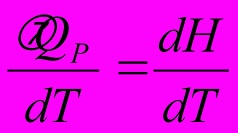
тепловой эффект:

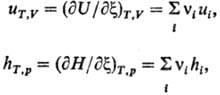
тепловой эффект:

2. Изменение температуры затвердевания различных растворов. Крио- скопический метод. Эбуллиоскопия.

С давлением насыщенного пара тесно связаны такие свойства растворов, как температура кипения и температура замерзания.

Жидкость закипает тогда, когда давление насыщенного пара над ней равно внешнему (атмосферному) давлению.

Жидкость замерзает тогда, когда давление ее насыщенного пара над жидкостью будет равно давлению насыщенного пара над твердой фазой (льдом).

Так как давление насыщенного пара над раствором меньше, чем над чистым растворителем (водой), то для закипания раствора требуется более высокая, а для замерзания – более низкая температура, чем для растворителя (воды).

II закон Рауля или следствия из I закона Рауля:

(Понижение температуры кристаллизации)

(Повышение температуры кипения)

Измерение температур кипения и замерзания растворов лежит в основе эбулиоскопического и криоскопического методов определения молярных (молекулярных) масс веществ.

или

Е– эбулиоскопическая (эбулиометрическая) константа

К – криоскопическая (криометрическая) константа.

Е и К зависят только от природы растворителя, но не от природы растворенного вещества.

3. Равновесие жидкость - пар в двухкомпонентных системах. Различ­ные виды диаграмм состояния. Законы Гиббса - Коновалова.

Газообразная фаза, находящаяся в равновесии с жидким раствором (насыщенный пар), содержит, в общем случае, все компоненты раствора, и давление насыщенного пара является суммой парциальных давлений компонентов: Р = Р1 + Р2

диаграмма состояния:

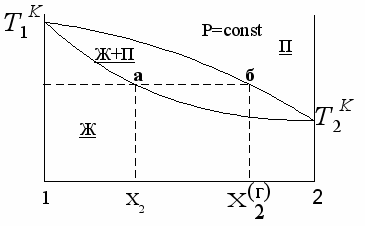
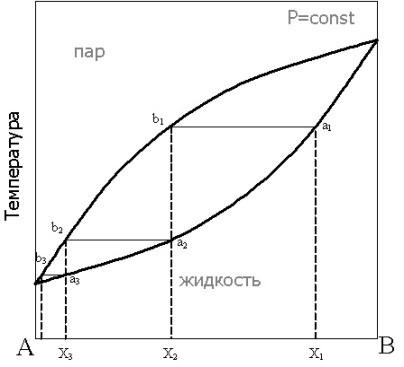
От диаграммы P – Х можно перейти к диаграмме температура кипения – состав при постоянном давлении, обычно атмосферном:

Законы Гиббса- Коновалова описывают процессы, протекающие в равновесных системах «жидкий раствор — пар» под действием температуры или давления.

Первый закон Коновалова (1881 г.) описывает процесс фракционной перегонки:

насыщенный пар по сравнению с равновесным раствором обогащён компонентом, добавление которого к системе повышает общее давление пара.

Второй закон Коновалова (1881 г.) описывает растворы с отклонениями от свойств идеальных растворов и объясняет существование азеотропных растворов, состав которых при перегонке не изменяется:

Экстремумы на кривых полного давления пара отвечают такому равновесию раствора и насыщенного пара, при котором состав обеих фаз одинаков.

Билет 16

1.Свобо́дная эне́ргия Гельмго́льца (или просто свобо́дная эне́ргия) — термодинамический потенциал, убыль которого в квазистатическомизотермическом процессе равна работе, совершённой системой над внешними телами

Свободная энергия Гельмгольца для системы с постоянным числом частиц определяется так:

• , где   — внутренняя энергия, 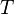  — абсолютная температура,   — энтропия.

Отсюда дифференциал свободной энергии равен:

• .

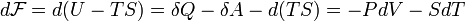Для системы с переменным числом частиц дифференциал свободной энергии Гельмгольца записывается так:

• ,

где   — химический потенциал, а   — число частиц в системе. При этом свободная энергия Гельмгольца для равновесного состояния записывается как функция  .

Свободная энергия Гиббса (или просто энергия Гиббса, или потенциал Гиббса, или термодинамический потенциал в узком смысле) — это величина, показывающая изменение энергии в ходе химической реакции и дающая таким образом ответ на вопрос о принципиальной возможности протекания химической реакции; это термодинамический потенциал следующего вида:

Классическим определением энергии Гиббса является выражение

где   — внутренняя энергия,   — давление,   — объём,   — абсолютная температура,   — энтропия.

Дифференциал энергии Гиббса для системы с постоянным числом частиц, выраженный в собственных переменных — через давление p и температуру T:

Для системы с переменным числом частиц этот дифференциал записывается так:

Здесь   — химический потенциал, который можно определить как энергию, которую необходимо затратить, чтобы добавить в систему ещё одну частицу

Уравне́ния Ма́ксвелла — система уравнений в дифференциальной или интегральной форме, описывающих электромагнитное поле и его связь сэлектрическими зарядами и токами в вакууме и сплошных средах. 

Дж.Максвелл (1831–1879) вывел следующие важные соотношения между переменными V, T, P и S:

2. ПАРЦИАЛЬНЫЕ МОЛЯРНЫЕ ВЕЛИЧИНЫ, термодинамич. величины, к-рые используют для описания концентрац. зависимостей св-в р-ров. Пусть М -нек-рая экстенсивная ф-ция состояния системы из h компонентов, т. е. св-во, зависящее от массы системы (объем, внутр. энергия, энтальпия, энтропия, энергия Гиббса, энергия Гельмгольца, теплоемкость и т.п.). Для i-го компонента П.м. в. M_i- определяется соотношением:

т.е. равна производной от величины M по числу молей m_i компонента i при постоянных т-ре T, давлении p и числах молей   всех остальных компонентов. Так, парциальный молярный объем

где V-объем системы; парциальная молярная энергия Гиббса (химический потенциал)

где G-энергия Гиббса системы.

Для приближенного определения используют графич. метод (см. рис.). В случае бинарной системы

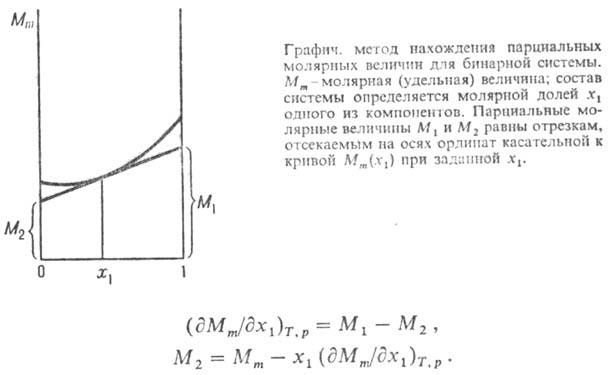
Изменения парциальных молярных величин при изменении состояния системы связаны между собой Гиббса-Дюгема уравнением, к-рое в обобщенном виде записывается след. образом:

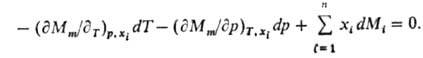
При Т, p = const (изотермо-изобарные условия)

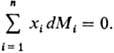
Согласно этому ур-нию, в бинарной системе парциальные молярные величины M₁ и M₂ при изменении состава изменяются в противоположных направлениях. Экстремумы на кривых M₁(x₁) и M₂(x₁), если таковые имеются, наблюдаются при одном и том же составе и противоположны по типу. Напр., для хим. потенциалов

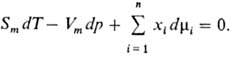 При T, p = const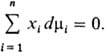

Это соотношение служит для расчета хим. потенциала компонента р-ра на основании концентрац. зависимости хим. потенциалов остальных компонентов, а также используется для проверки на термодинамич. согласованность эксперим. данных о зависимостях хим. потенциалов от состава, т-ры и т.п.

ГИББСА - ДЮГЕМА УРАВНЕНИЕ - термодинамич. соотношение между приращениями темп-ры T, давления P и хим. потенциалов   многокомпонентной термодинамич. системы:  , где S - энтропия, V - объём, N_i - число частиц i-го компонента.

3. Фазовые диаграммы двухкомпонентных систем обычно представляют следующим образом: на оси ординат откладывают температуру, а на оси абсцисс — состав. Состав можно выражать различными способами: мольным отношением, мольными долями, весовыми долями или массовыми процентами. Традиционно состав выражают массовыми процентами, реже пользуются мольными соотношениями. Такие диаграммы имеют тот недостаток, что невозможно непосредственно узнать молярный состав, но поскольку стехиометрические комплексы встречаются в данных системах довольно редко, это не так уж существенно. Массовые шкалы обеспечивают более удобное разделение площади диаграммы на зоны стабильности различных фаз. Кроме того, такое представление фазовой диаграммы единственно возможно в том случае, если состав ПАВ точно неизвестен.