Экзаменационный билет № 1

1. Уравнения состояния идеального и реальных газов. Уравнение Ван-дер-Ваальса.

Уравнение состояния идеального газа: pV = nRT

Где p — давление; V — объем; T — абсолютная температура газа (в градусах Кельвина);R — универсальная газовая постоянная, общая для всех газов;

n = — количество вещества.

Или pVm=RT, где

Vm — молярный объём.

Реальный газ — газ, который не описывается уравнением состояния идеального газа Клапейрона — Менделеева.

Зависимости между его параметрами показывают, что молекулы в реальном газе взаимодействуют между собой и занимают определенный объём. Состояние реального газа часто на практике описывается обобщённым уравнением Менделеева — Клапейрона:

где p — давление; V — объем; T — температура; Zr = Zr (p,T) — коэффициент сжимаемости газа; m — масса; М — молярная масса; R — газовая постоянная.

Наиболее простым и качественно верно отображающим поведение реального газа, является уравнение Ван-дер-Ваальса.

Для одного моля газа Ван-дер-Ваальса оно имеет вид:

Где p — давление; V — молярный объём; T — абсолютная температура; R — универсальная газовая постоянная; b – поправка на объём; a/V^2 –поправка на давление.

Уравнение Ван-дер-Ваальса качественно верно отображает поведение жидких и газообразных веществ, для двухфазных состояний оно неприменимо.

2. Давление насыщенного пара жидких растворов. Закон Рауля и его термодинамический вывод. Неидеальные растворы и их свойства. Метод активностей. Коэффициенты активности и их определение по парциальным давлениям компонента.

Давление насыщенного пара жидких растворов. Закон Рауля и его термодинамический вывод.

Первый закон Рауля:

Парциальное давление насыщенного пара компонента раствора прямо пропорционально его мольной доле в растворе, причем коэффициент пропорциональности равен давлению насыщенного пара над чистым компонентом.

В бинарной смеси вещества х1+х2=1:

Относительное понижение парциального давления пара растворителя над раствором равно мольной доле растворенного вещества и не зависит от природы растворенного вещества.

Термодинамический вывод.

, где

μА(р) - химический потенциал растворителя в растворе

XА - мольной долей растворителя в растворе

, где

μА(п) - химический потенциал растворителя в паре

РА - парциальное давление пара растворителя

, где

μ*А - химический потенциал чистого жидкого растворителя

μ°А(п) - химический потенциал равновесного пара

В состоянии равновесия μА(п) = μА(р) получим:

Принимая, что μ*А = μ°А(р), получаем следующее уравнение:

=> =>

Неидеальные растворы - все жидкие смеси обладают свойствами, которые в большей или меньшей степени отклоняются от свойств идеальных растворов.

Отклонения от идеальных свойств могут быть положительными и отрицательными. Если давление пара над реальным раствором больше, чем над идеальным, то отклонения положительны, а если меньше, то отрицательны.

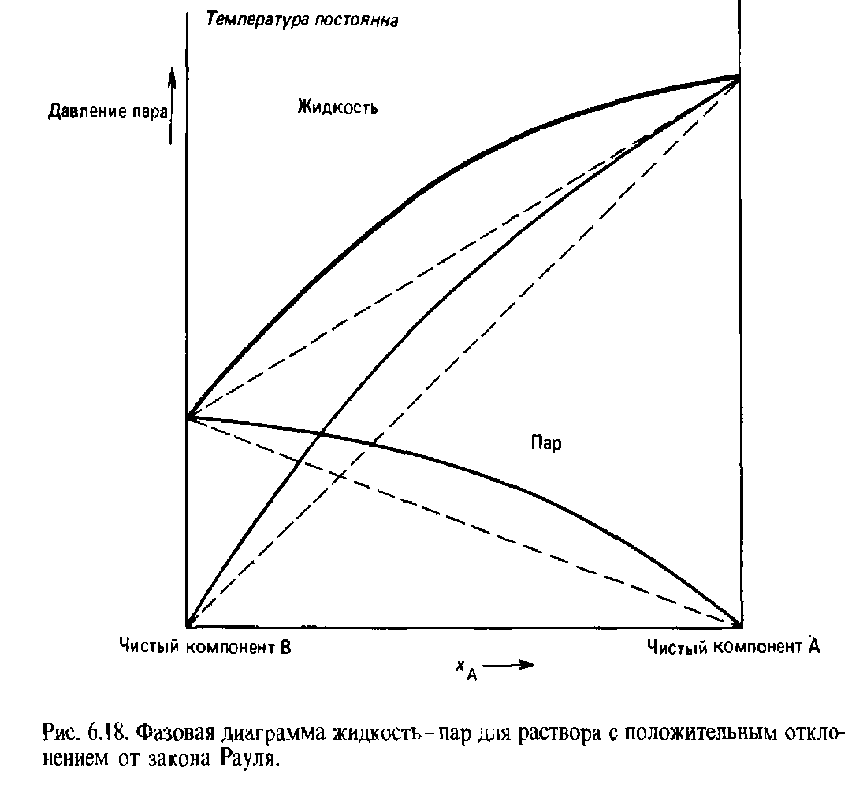
Положительное отклонение отрицательное отклонение

Метод активностей. Коэффициенты активности и их определение по парциальным давлениям компонент.

Активность компонентов раствора — эффективная (кажущаяся) концентрация компонентов с учётом различных взаимодействий между ними в растворе, то есть с учётом отклонения поведения системы от модели идеального раствора.

Активность была предложена в 1907 году Льюисом как новая переменная, применение которой вместо концентрации позволяет использовать для описания свойств реальных растворов относительно простые уравнения, полученные для идеальных систем. Альтернативой этому пути является использование более сложных уравнений, учитывающих взаимодействие между частицами. Активность отличается от общей концентрации на некоторую величину.

Отношение активности к общей концентрации вещества в растворе называется коэффициентом активности:

Коэффициент активности служит мерой отклонения поведения раствора (или компонента раствора) от идеального.

Размерность и величина активности зависит от используемого способа выражения концентрации [моль/л] и [моль/кг].

Методы определения активности:

1. По равновесному давлению пара

2. По повышению температуры кипения раствора

3. По понижению температуры замерзания раствора

4. По осмотическому давлению раствора

5. По распределению компонента между конденсированными фазами

6. По равновесию химической реакции с газовой фазой

7. По значению э. д. с. гальванического элемента

Методы определения активности по парциальным давлениям компонентов (по равновесному давлению пара)

В основе этого метода лежит соотношение:

Где

— парциальное давление пара компонента над раствором,

— давление пара этого компонента для стандартного состояния.

Соответственно, если за стандартное состояние принято состояние чистого компонента, то .

3. Различные диаграммы состояния двухкомпонентных систем и их анализ на основе правила фаз.

В двухкомпонентной системе, согласно правилу фаз Гиббса в равновесии может одновременно находится не более четырех фаз – нонвариантная система (f=0). Максимальное число степеней свободы равно трем, т. е. не нарушая фазового соотношения в такой системе в определенных переделах можно изменять три параметра состояния (давление, температуру и состав). Поэтому для полного описания диаграмм состояния двухкомпонентных систем необходимо использовать пространственную систему координат, что не всегда удобно. Чаще всего один из параметров (давление или температура) фиксируется, и диаграмму состояния представляют в двумерной плоскости.

Наибольшее распространение получили диаграммы плавкости, передающие зависимость температур равновесия твердых и жидких фаз (т.е. температур плавления), а также температур равновесия твердых фаз от состава системы. Вид диаграмм состояния зависит от природы веществ. Диаграммы состояния, компоненты которых неограниченно растворяются друг в друге как в жидком так и в твердом состояниях, аналогичны диаграммам состояния бинарных жидких растворов, при этом области жидкого расплава первых диаграмм отвечает область пара вторых а области твердых сплавов первых - области жидкости вторых и т.д.

Наиболее простыми являются диаграммы состояния, составляющие компоненты которых неограниченно растворимы друг в друге в жидком состоянии и совершенно не растворяются в твердом (рис.4.1 “а”), так называемые диаграммы состояния эвтектического типа. Диаграмма несколько усложняется, когда компоненты, неограниченно растворяющиеся в жидком состоянии, частично растворяются друг в друге и в твердом состоянии (рис.4.1 “б”).

Диаграмма состояния двухкомпонентной системы эвтектического типа: а) компоненты нерастворимы в твердом состоянии: б) компоненты частично растворимы в твердом состоянии.

Диаграммы состояния сплавов строятся на основании опытных данных.

Рассмотрение и понимание диаграмм состояния облегчается при использовании правила фаз Гиббса. В соответствии с этим правилом число фаз равновесной гетерогенной системы Ф, число степеней свободы f и число компонентов k связаны соотношением

Числом степеней свободы f называют число переменных, которое можно изменить, не нарушая равновесия в системе, т.е. не вызывая исчезновения имеющихся фаз или появления новых. Степени свободы – это температура, давление, концентрации компонентов в любой из сосуществующих фаз.

Рис.4.2. Диаграммы состояния двухкомпонентной системы c промежуточными химическими соединениями: а) соединение AnBmплавится конгруентно; б) соединение AnBmплавится инконгруентно.

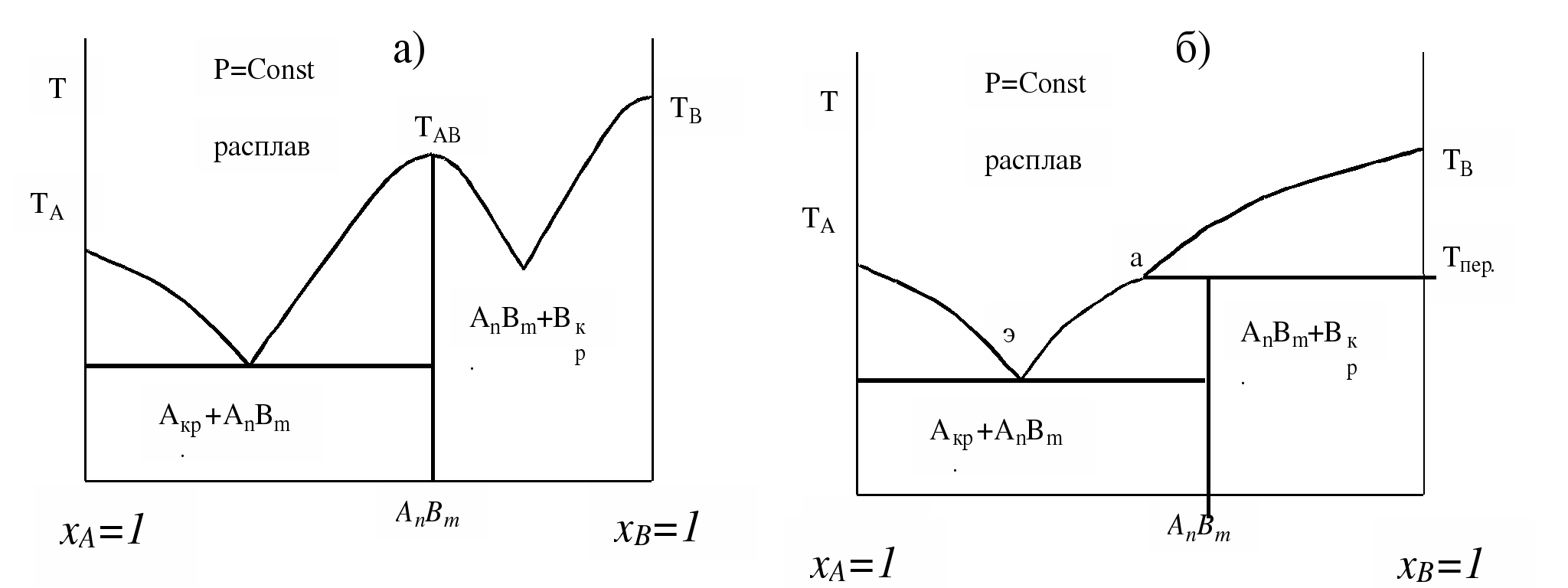
Ограничим рассмотрение диаграмм состояния, например, металлическими системами. Упругость пара над металлическими сплавами, даже находящимися в жидком состоянии, невелика. Поэтому наличием пара в таких системах пренебрегают и рассматривают их как системы, состоящие только из жидких и твердых фаз. Такие системы называют конденсированными. Как показывают расчеты на основании уравнения Клаузиуса-Клапейрона, небольшие изменения давления, с которыми на практике приходится иметь дело, на температурные равновесия фаз в конденсированных системах заметного влияния не оказывают. Поэтому давление как фактор, влияющий на равновесие конденсированных систем, можно не учитывать; величину 2 в уравнении (4.1) следует заменить на 1, т.е. использовать правило фаз для таких систем в виде

(4.1а)

Рис.4.3. а) Кривые охлаждения чистых металлов и сплавов. б) Диаграмма состояния системы АВ, построенная по этим кривым охлаждения.

4. Плотность 50% (по массе) раствора этанола в воде при 25°С равна 0.914 г∙см-3. Рассчитайте парциальный мольный объем этанола в этом растворе, если парциальный мольный объем воды равен 17.4 см3∙моль-1.

M1(H2O)=18 г/моль

M2(C2H5OH)=46 г/моль

Экзаменационный билет № 2

1. Теплота и работы различного рода. Работа расширения для различных процессов.

Теплота – это количество переданной энергии системе внешними телами путем теплообмена.

Работа – это процесс передачи энергии системе от внешних тел.

Изохорный процесс (V=const): A=0

Изобарный процесс (P=const): , т.к pV=RT.

Изотермический процесс (T=const):

Адиабатный процесс (Q=0): A=-U

2. Изменение температуры затвердевания различных растворов. Криоскопия.

Температура замерзания зависит от концентрации раствора. Увеличивая концентрацию раствора, мы будем уменьшать температуру кристаллизации. Самую низкую температуру замерзания имеет насыщенный раствор.

Раствор замерзает не так, как простая жидкость. Процесс его замерзания растягивается на большой температурный интервал.

Криоскопия – метод исследования вещества, основанный на наблюдении t° замерзания растворов. Как было известно уже давно, t° замерзания растворов лежит ниже t° замерзания соответствующего чистого растворителя.

Благден (1788) установил, что понижение t° замерзания, представляющая собой разность между t° замерзания чистого растворителя и t° замерзания раствора, пропорциональна количеству растворенного вещества. Позднее Рюдорф (1861—62) самостоятельно пришел к тем же результатам, а Коппе (1871—72) подтвердил и дополнил предыдущие исследования, обнаружив, что сходные по свойствам вещества, растворенные в одном и том же объеме воды в количествах, пропорциональных их молекулярным весам, вызывают приблизительно одно и то же понижение темп, замерзания.

Основная работа была выполнена Раулем (1882—84), который распространил исследования на целый ряд органических соединений, пользуясь ими как в качестве растворяемых веществ, так и в качестве растворителей; для всех таких растворов, взятых в слабой концентрации, Рауль окончательно установил следующие два положения:

1) понижение t° замерзания раствора какого-либо вещества в данном растворителе прямо пропорционально концентрации раствора;

2) понижения t° замерзания, наблюдаемые в растворах, содержащих по 1 г различных веществ на 100 г данного растворителя, обратно пропорциональны молекулярным весам растворенных веществ. Отсюда следует, что молекулярное понижение t° замерзания, т. е. то понижение, которое наблюдалось бы в растворе, содержащем 1 грамм-молекулу вещества в 100 г растворителя, есть величина постоянная, характерная для данного растворителя.

3. Изотерма Вант-Гоффа. Изменение энергии Гиббса и энергии Гельмгольца при химической реакции.

Изотерма Вант-Гоффа: aА + bВ = cC +dD - произвольной химическая реакция

Где

ΔG - изменение энергии Гиббса;

T — абсолютная температура газа;

R — универсальная газовая постоянная.

Где

Pa,Pb,Pc,Pd – равновесные значения активных концентраций;

Выражение под знаком логарифма, представляющее собой отношение произведения равновесных активностей продуктов к произведению активностей исходных веществ в степенях их стехиометрических коэффициентов, называется константой равновесия.

Изменение энергии Гиббса и энергии Гельмгольца при химической реакции.

1. , ;

2. 

при условии, что T=298K;

3. ,

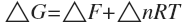где Δn – изменение количества вещества.

4. Диаграмма плавкости системы Sn-Zn показана на рис. Определить: 1) сколько степеней свободы имеет система в точках a, b и c; 2) состав расплава, начинающего затвердевать при 300° С; 3) сколько цинка выделится из 1 кг 60%-ного расплава, если его охладить до 300° С; 4) сколько эвтектики полу-чится из 100 г 5%-, 30%- и 80%-ного расплавов.

Экзаменационный билет № 3

1. Первый закон термодинамики. Внутренняя энергия. Энтальпия. Закон Гесса и его следствия. Стандартные состояния и стандартные теплоты химических реакций. Теплота сгорания. Теплоты образования.

Первый закон термодинамики.

• Подводимое к системе тепло расходуется на изменение внутренней энергии и на совершение работы этой системы.

• Вечный двигатель первого рода не возможен, т.е. не возможно построить машину, которая давала бы работу не затрачивая при этом энергию.

Внутренняя энергия (U) - сумма потенциальной энергии взаимодействия частиц между собой и кинетической энергии их движения, т.е. внутренняя энергия складывается из энергии поступательного и вращательного движения в молекуле.

Энтальпия (H) — это свойство вещества, являющееся мерой энергии, накапливаемой веществом при его образовании. Размерность энтальпии [кДж/моль].

Закон Гесса.

Тепловой эффект химической реакции, проводимый в изобарно-изотермических или изохорно-изотермических условиях, зависит только от вида и состояния исходных веществ и продуктов и не зависит от пути её протекания.

Следствия закона Гесса.

1). Тепловой эффект прямой реакции равен по величине и противоположен по знаку тепловому эффекту обратной реакции.

2). Для двух компонентов реакции, имеющих одинаковые исходные, но разные конечные состояния, разность тепловых эффектов представляет собой тепловой эффект перехода из одного конечного состояния в другое.

3). Для двух реакций, имеющих одинаковые конечные, но разные исходные состояния, разность тепловых эффектов представляет собой тепловой эффект перехода из одного исходного состояния в другое.

4). Тепловой эффект химической реакции равен разности сумм теплот образования продуктов реакции и исходных веществ, умноженных на стехиометрические коэффициенты.

Стандартные состояния - условно принятые термодинамические состояния индивидуальных веществ и компонентов растворов. Представление о С.С. введено в связи с тем, что простые термодинамические закономерности не описывают достаточно точно поведение реальных веществ, когда количественной характеристикой служит давление р или концентрация с.

Стандартная теплота образования – это тепловой эффект реакции образования 1 моль сложного вещества из простых.

Теплота сгорания – это тепловой эффект реакции окисления 1 моль вещества в избытке кислорода до высших устойчивых оксидов.

Теплота растворения – это тепловой эффект процесса растворения 1 моль вещества в бесконечно большом количестве растворителя.

2. Термодинамическая классификация растворов. Функции смешения для идеальных и неидеальных растворов. Предельно разбавленные растворы, регулярные, строго регулярные растворы и их свойства.

Термодинамическая классификация растворов

Как известно из курса физической химии, классифицируя растворы по термодинамическим свойствам, выделяют идеальные и неидеальные растворы. В свою очередь, в группе неидеальных различают предельно разбавленные, регулярные, атермальные и некоторые другие типы растворов. Термодинамическая классификация растворов основана на характере уравнений для химических потенциалов компонентов растворов.

Термодинамические свойства раствора в широкой области концентраций можно описать с помощью функций смешения. Если Ф – молярное значение некоторой экстенсивной функции, а – молярная функция смешения, то по определению

где – молярное значение термодинамической функции Ф для чистого компонента.

Предельно разбавленные растворы – это раствор, в котором свойства растворителя практически остались неизменными по сравнению с чистым растворителем ввиду низкой концентрации раствора, в то время как свойства растворенного вещества могут очень сильно отличаться от его свойств в чистом виде ввиду попадания в среду растворителя. Свойствами п.р. растворов обладают обычно все разбавленные растворы вплоть до определенной концентрации, характерной для каждой системы. Чем ближе свойства компонентов, тем до более высокой концентрации сохраняют их растворы свойства п.р. растворов. Для растворов электролитов этот предел очень низок, так как ионы заметно изменяют свойства растворителя уже при миллимолярных концентрациях.

Регулярными называют растворы, при образовании которых изменение энтропии равно этой же величине для идеального раствора и рассчитывается по уравнению (2.1), изменение объема не происходит, а парциально молярная теплота смешения компонента не равна нулю

Наличие теплоты смешения является единственной причиной отклонения поведения регулярных растворов от идеальности.

К числу наиболее простых решеточных теорий растворов относят теорию строго регулярных растворов. Основной параметр этой теории – энергия взаимообмена (12 ) реакции образования единичной связи 1-2. Она характеризует различие в энергиях взаимодействия одинаковых молекул и разносортных и определяется соотношением

, где и – энергия потенциального взаимодействия частиц

Наиболее простые соотношения выводят в предположении, что линейно меняется с составом.

Принципиальным недостатком теории строго регулярных растворов является допущение о том, что изменение объема при смешении равно нулю.

Еще одна группа растворов по термодинамической классификации – атермальные растворы. Это растворы, для которых характерно заметное изменение объема и отсутствие тепловых эффектов при смешении компонентов.

3. Однокомпонентные системы. Фазовые переходы первого рода. Диаграмма состояния серы. Уравнение Клайперона–Клаузиуса и его применение к различным фазовым переходам первого рода.

Однокомпонентные системы содержат лишь одно вещество, которое может находиться в разных агрегатных состояниях.

Фазовые переходы первого рода — фазовые переходы, при которых скачком изменяются первые производные термодинамических потенциалов (s,v) по интенсивным параметрам системы (температуре или давлению). Переходы первого рода реализуются как при переходе системы из одного агрегатного состояния в другое, так и в пределах одного агрегатного состояния (в отличие от фазовых переходов второго рода, которые происходят только в пределах одного агрегатного состояния).

Первые производные химического потенциала :

Примеры фазовых переходов первого рода: плавление и кристаллизация, испарение и конденсация, сублимация и десублимация.

Фазовая диаграмма серы

Кристаллическая сера существует в виде двух модификаций – ромбической (Sр) и моноклинной (Sм). Поэтому возможно существование четырех фаз: ромбической, моноклинной, жидкой и газообразной (рис.2). Сплошные линии ограничивают четыре области: пара, жидкости и двух кристаллических модификаций. Сами линии отвечают моновариантным равновесиям двух соответствующих фаз. Заметьте, что линия равновесия моноклинная сера - расплав отклонена от вертикали вправо ( сравните с фазовой диаграммой воды ). Это означает, что при кристаллизации серы из расплава происходит уменьшение объема. В точках А, В и С в равновесии сосуществуют 3 фазы (точка А – ромбическая, моноклинная и пар, точка В – ромбическая, моноклинная и жидкость, точка С – моноклинная, жидкость и пар). Легко заметить, что есть еще одна точка О, в которой существует равновесие трех фаз – перегретой ромбической серы, переохлажденной жидкой серы и пара, пересыщенного относительно пара, равновесного с моноклинной серой. Эти три фазы образуют метастабильную систему, т.е. систему, находящуюся в состоянии относительной устойчивости. Кинетика превращения метастабильных фаз в термодинамически стабильную модификацию крайне медленна, однако при длительной выдержке или внесении кристаллов-затравок моноклинной серы все три фазы все же переходят в моноклинную серу, которая является термодинамически устойчивой в условиях, отвечающих точке О. Равновесия, которым соответствуют кривые ОА, ОВ и ОС (кривые – возгонки, плавления и испарения, соответственно) являются метастабильными.

В случае диаграммы серы мы сталкиваемся с самопроизвольным взаимным превращением двух кристаллических модификаций, которые могут протекать в прямом и обратном направлении в зависимости от условий. Такого типа превращения называются энантиотропными (обратимыми).

Взаимные превращения кристаллических фаз, которые могут протекать лишь в одном направлении, называются монотропными (необратимыми). Примером монотропного превращения является переход белого фосфора в фиолетовый.

Уравнение Клайперона–Клаузиуса и его применение к различным фазовым переходам первого рода.

Уравнение Клайперона–Клаузиуса - термодинамическое уравнение, относящееся к процессам перехода вещества из одной фазы в другую (испарение, плавление, сублимация, полиморфное превращение и др.).

Для описания фазового перехода первого рода необходимо определить зависимость давления от температуры в точках фазового перехода: P = P(T), то есть форму кривой равновесия двух фаз. Применение методов равновесной термодинамики позволяет определить первую производную этой зависимости, или наклон кривой равновесия.

На основании первой теоремы Карно можно записать выражение для к.п.д. рассматриваемого цикла:

(1)

где δA12– совершаемая за цикл работа. С учетом бесконечной малости величины dP в первом приближении можно считать, что работа δA12, совершаемая за цикл Карно близка к работе цикла, представляющего собой прямоугольник бесконечно малой высоты. Это позволяет заменить адиабаты на боковых сторонах цикла Карно вертикальными отрезками при V = const, то есть представить цикл Карно в виде прямоугольника, высота которого равна бесконечно малой величине dP. В этом приближении имеем:

(2)

Фазовые переходы первого рода количественно характеризуются величиной удельной теплоты фазового перехода, которая численно равна количеству теплоты сообщаемой единице массы вещества для осуществления фазового перехода:

(3)

Тогда с учетом формул (2) и (3) выражение (1) можно преобразовать к виду:

(4)

Или:

(5)

Это выражение называется уравнением Клапейрона–Клаузиуса. Оно позволяет определить производную давления от температуры при равновесном фазовом переходе первого рода в зависимости от удельной теплоты перехода, его температуры и удельных объемов начальной и конечной фаз.

4.При каком равновесном давлении должен находиться PCl5 при 250°С, чтобы степень его превращения в PCl5 и Cl2 составила 30%? Для реакции PCl5(газ) = PCl5(газ) + Cl2(газ) при 250° С K0=1,78.

Билет №5

Вопрос 1.

Энтропия, функция состояния S термодинамической системы, изменение которой dS для бесконечно малого обратимого изменения состояния системы равно отношению количества теплоты   полученного системой в этом процессе (или отнятого от системы), к абсолютной температуре Т:

Понятие энтропии как функции состояния системы постулируется вторым началом термодинамики, которое выражает через энтропию различие между необратимыми и обратимыми процессами. Для первых dS>δQ/T для вторых dS=δQ/T.

Вопрос 2.

Газообразная фаза, находящаяся в равновесии с жидким раствором / насыщенный пар /, содержит, в общем случае, все компоненты раствора. Однако, часто встречаются та­кие системы, в которых один или несколько компонентов нелетучи; поэтому содержанием их в газовой фазе пренебрегают. При Небольших давлениях насыщенный пар можно считать идеальным газом, следовательно в соответствии с законом Дальтона общее давление пара над раствором равно сумме парциальных давлений веществ, составляющих данную систему. Для бинарного раствора общее давление пара P будет равно: P = P₁ +P₂ (1) где Р₁ и P₂ - парциальные давления. Суммарное давление насыщенного пара к парциальные давления являются функциями температуры и состава раст­вора. В простейшем случае зависимость парциального давления от состава выражается уравнением:  P_i = P_i⁰ N_i^ж = P N_i^газ (2) здесь: N_i^газ и N_i^ж -мольные доли i-го компонента соответственно в растворе и в паровой фазе. P_i⁰- давление пара над чистым i-м компонентом. Ив уравнения (2 ) следует: 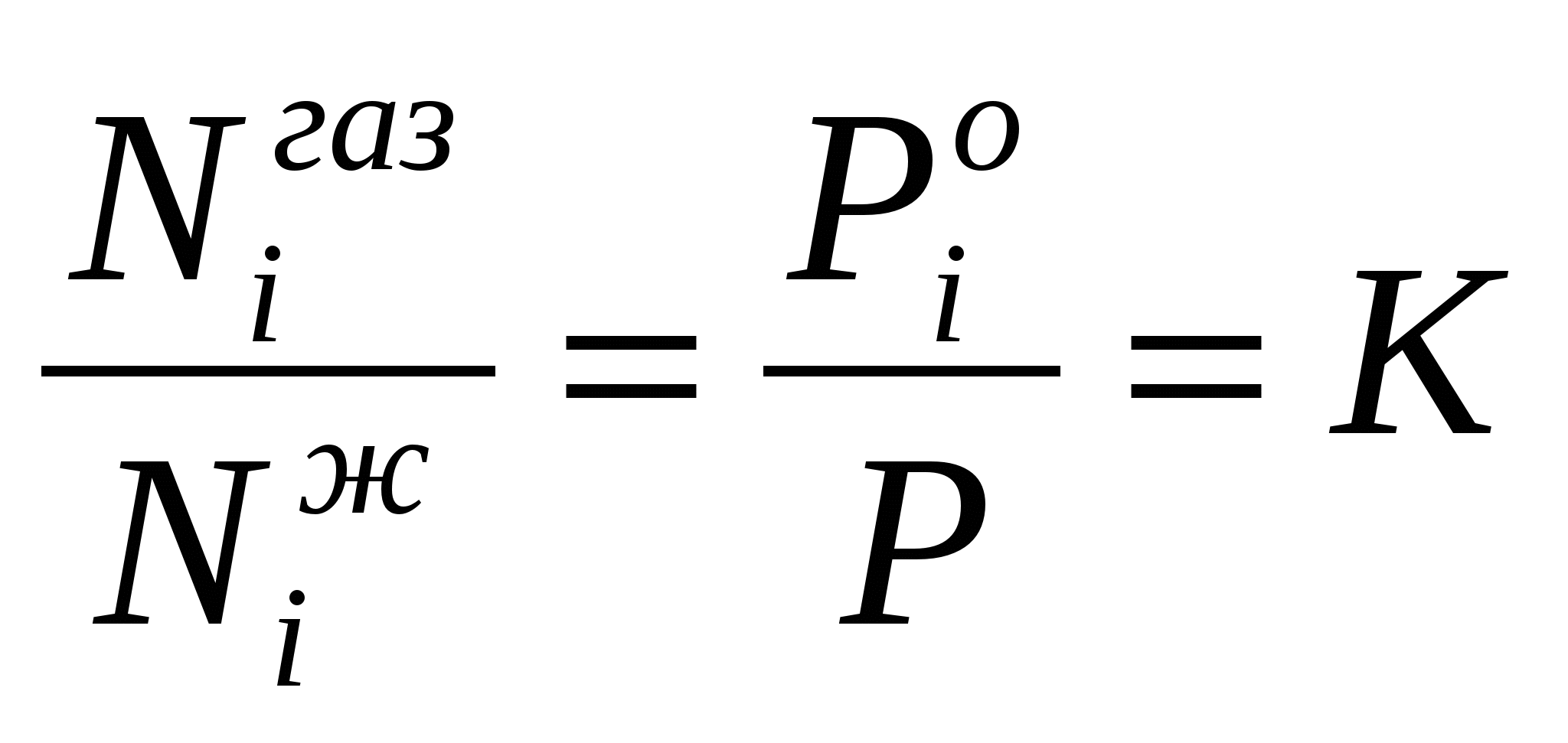 (3) Константа К характеризует распределение данного компонента между паровой к жидкой фазами и называемся константой фазо­вого равновесия. Применив уравнение (2) к бинарному раствору, получим:  (4) Из уравнения (4) следует, что в идеальных растворах состав пара отличается от состава жидкости если величины давления пара над чистыми веществами не равны друг другу. Ес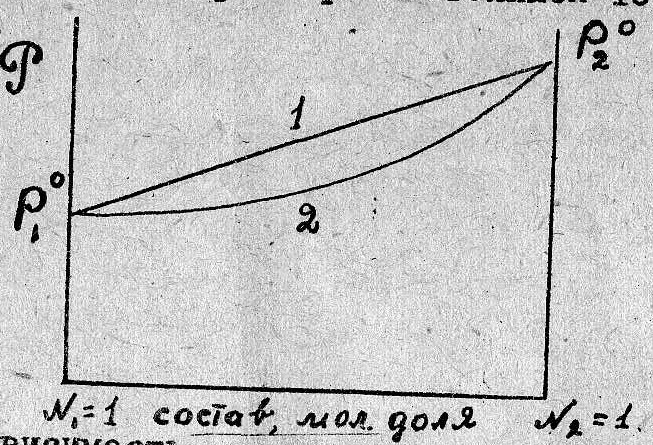 ли Р₁⁰ > Р₂¹ , то N₁^газ > N₂^газ  Рис 1. Следовательно, пар относительно богаче тем веществом, при добавление которого к жидкой смеси повышается общее давление пара над раствором или при данном давлении снижает его температуру кипения. (Первый закон Коновалова Д.П.)  На рис. 1 приведена зависимость давления насыщенного пара от состава жидкости /прямая 1/ и состава пара /кривая 2 / для идеальных растворов при постоянной температуре. В реальных растворах наблюдаются отклонения, за счёт взаимодействия между частицами. Отклонения в сторону больших значений принято называть положительными, а в сторону меньших – отрицательными.  С увеличением отклонения на кривых зависимости давле­ния пара - состав может появиться минимум (отрицательное отклонение) или максимум (положительное отклонение). Чем больше разность значений Р₁⁰ и P₂⁰ кем большими должны быть отклонения для образования максимума или мини­мума Минимум на кривых давление пара состав характерен для веществ способных к диссоциации, максимум – для веществ способных к ассоциации. 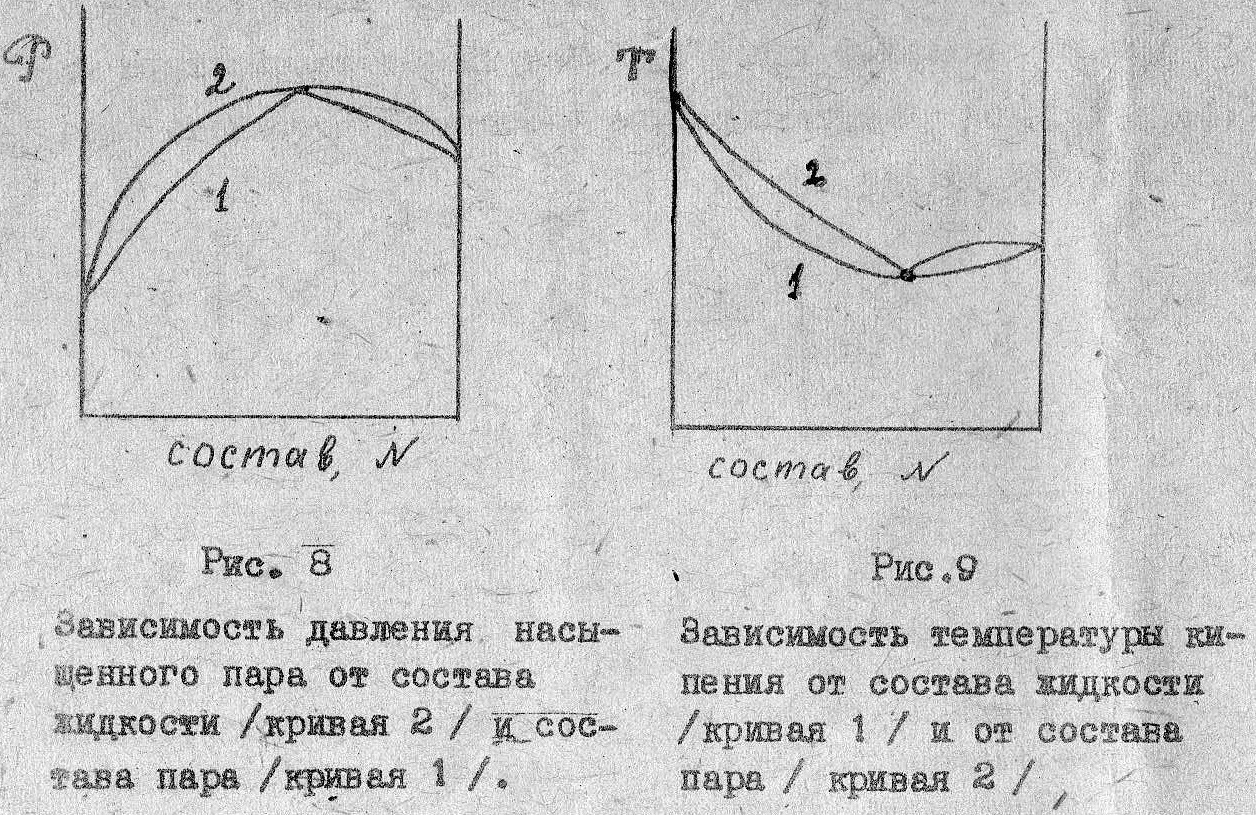М инимуму на диаграмме давление – состав отвечает максимум на диаграмме температура – состав (рис 8 и 9) Ии наоборот, максимуму на диаграмме давление состав будет соответствовать минимум на диаграмме температура состав.  В точках экстремума давление пара или температура кипения, составы жидкости и пара совпадают. (второй закон Коновалова Д.П.)

КОНОВАЛОВА ЗАКOНЫ, связывают изменения состава равновесно сосуществующих жидкой и паровой фаз двойной системы с изменениями т-ры или давления. В совр. формулировке первый Коновалова закон устанавливает: при постоянной т-ре Т = const давление пара р-ра возрастает (уменьшается) при увеличении концентрации того компонента, содержание к-рого в паре больше (меньше), чем в р-ре; при постоянном давлении р = const т-ра кипения р-ра возрастает (уменьшается) при увеличении концентрации того компонента, содержание к-рого в паре меньше (больше), чем в р-ре. Второй Коновалова закон: в точке экстремума на кривой зависимости равновесного давления от состава р-ра (пара) при Т=const или на кривой концентрационной зависимости т-ры кипения (конденсации) при р=const составы сосуществующих в равновесии жидкости и пара совпадают. Экстремумы на кривых р(х)при Т=const и Т(х) при р=const (х-молярная доля одного из компонентов) наблюдаются при одинаковом составе; еслидавление имеет максимум, то т-ра - минимум, и наоборот. Третий Коновалова закон: при постоянных т-ре или давлении изменение составов жидкого р-ра и пара происходит в одном направлении (симбатно). Коновалова законы справедливы вдали от критического состояниярассматриваемой системы. Они теоретически обоснованы и экспериментально подтверждены для двойных систем, состоящих из жидкой и паровой фаз, Д. П. Коноваловым в 1881-84 независимо от Дж. Гиббса, к-рым в 1876-78 были высказаны более общие положения. Установлено (А. В. Сторонкин, А. Г. Морачевский, 1959), что при определенных способах изменения состава первый и третий Коновалова законы справедливы и длямногокомпонентных систем. Второй Коновалова закон часто наз. законом Гиббса-Коновалова; он справедлив для систем с любым числом компонентов. Законы, аналогичные Коновалова законам, могут быть сформулированы применительно к равновесиям твердый р-р - пар и твердый р-р - жидкий р-р (для последних обычно рассматривают диаграммы состояния в координатах Т—х при р=const). Коновалова законы играют важную роль при построении диаграмм фазового равновесия, анализе эксперим. данных о равновесии жидкость - пар, разработке методов ректификац. разделения в-в.