Властивості визначників.

Нижче сформулюємо і доведемо деякі властивості визначників 2–го порядку. Зазначимо, що всі ці властивості справедливі для визначників будь-якого порядку.

1. При транспонуванні визначник не змінюється.

Дійсно:

Наслідок. У визначнику рядки та стовпці мають однакові властивості (рівноправні), тому надалі у формулюваннях будемо говорити „ряд”, розуміючи під цим словом „елементи деякого рядка або деякого стовпця” визначника.

2. Якщо у визначнику поміняти місцями будь-які два паралельних ряди, то визначник змінить знак на протилежний.

3. Якщо визначник має два однакових паралельних ряди, то він дорівнює нулю.

4. Для того щоб помножити визначник на число, потрібно помножити на це число деякий один його ряд.

Наслідок 1. Спільний множник усіх елементів будь-якого ряду виноситься за знак визначника.

Наслідок 2. Визначник, у якому є нульовий ряд, дорівнює нулю.

Наслідок 3 (із властивостей 3, 4). Визначник, у якого є два паралельних пропорційних ряди, дорівнює нулю.

5. Якщо у визначнику елементи деякого ряду є сумою двох доданків, то він дорівнює сумі двох визначників, наприклад:

6. Визначник не зміниться, якщо до всіх елементів будь-якого ряду додати відповідні елементи паралельного ряду, помножені на одне й те саме число.

Дійсно, застосувавши попередні властивості, отримаємо:

.

Зауваження. Властивість 6 дозволяє перетворювати в нуль деякі елементи визначника, не змінюючи його величини. Це часто застосовують для спрощення обчислень.

Наприклад, обчислити визначник .

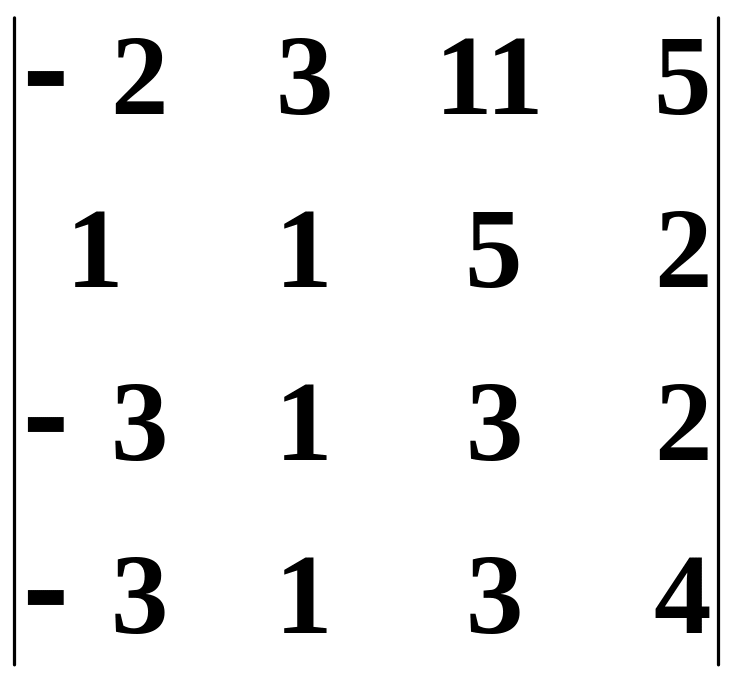„Зробимо” якомога більше нульових елементів, наприклад у 1–ому стовпці. Для цього працюємо з 2–им рядком (оскільки є елемент, рівний 1): домножимо його на 2 і додамо до 1–го рядка, а потім домножимо його на 3 і додамо до 3–го і 4–го рядків.

7. Сума добутків елементів будь-якого ряду визначника на алгебраїчні доповнення елементів паралельного ряду дорівнює нулю (іноді цю властивість називають другою теоремою розкладу визначника).

Дійсно, якщо , то, наприклад,

8. Визначник добутку двох квадратних матриць одного порядку дорівнює добутку їх визначників.

.

9. Визначник трикутної (верхньої або нижньої), діагональної матриці дорівнює добутку діагональних елементів:

.

Зокрема, визначник одиничної матриці дорівнює одиниці:

.

Завдання для розв’язування.

Обчислити визначники:

а)

б)

в)

г)

д)

ж) ;

з) ;

е) .

Обернена матриця.

Повернемось до операції «ділення матриць» (яку визначимо як добуток на обернену матрицю).

Нехай – ­­квадратна матриця порядку .

Означення. Матриця називається оберненою до матриці , якщо

- одинична матриця.

Зауваження. Очевидно, що – квадратна матриця того ж порядку, що і .

Означення. Квадратна матриця називається невиродженою, якщо її визначник . У супротивному випадку матриця називається виродженою.

Справедлива наступна

Теорема. Для існування оберненої матриці до квадратної матриці необхідно і достатньо, щоб її визначник (тобто матриця повинна бути невиродженою).

Доведення.

Схема знаходження оберненої матриці.

1. Знаходимо визначник матриці . Якщо 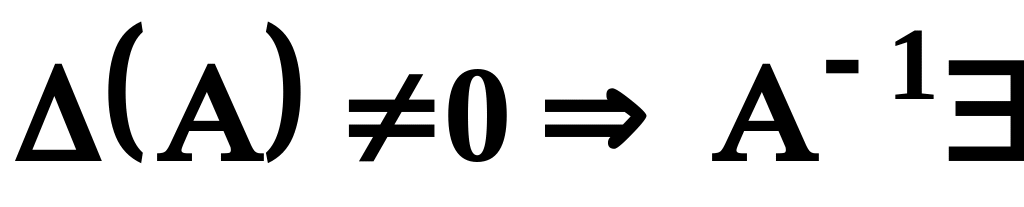, якщо ж - вироджена, і не .

2. Знаходимо – алгебраїчні доповнення усіх елементів визначника.

3. Записуємо обернену матрицю:

.

4. Якщо потрібно, виконуємо перевірку:

(або ).

Наприклад, знайти обернену для матриці

.

Розв’язування.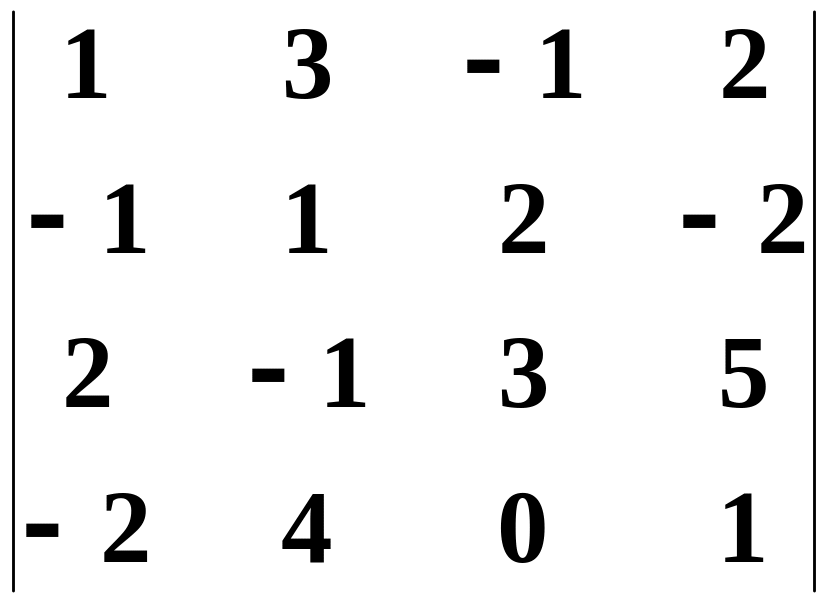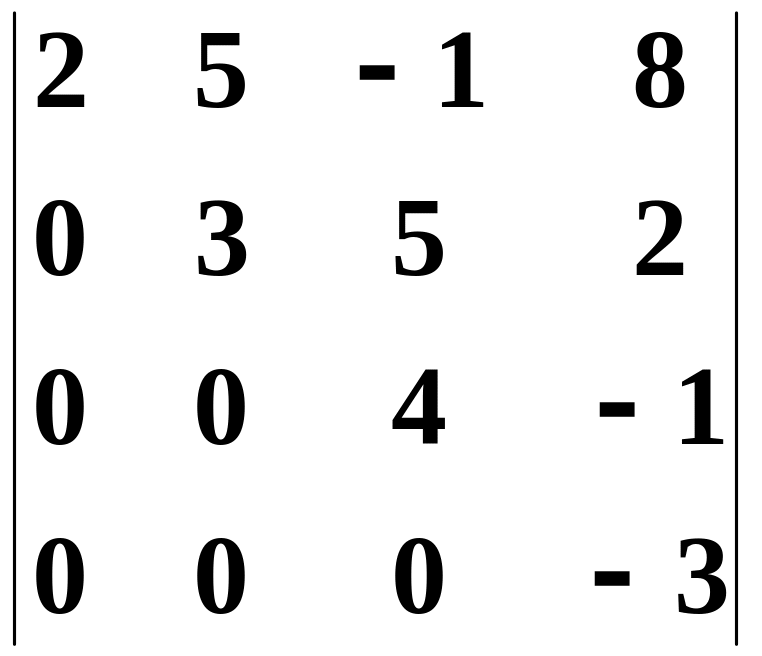