Арифметичні теореми для збіжних послідовностей.

Теорема. Якщо послідовності та - збіжні, причому , , то:

1. .

2. .

3. Якщо , то .

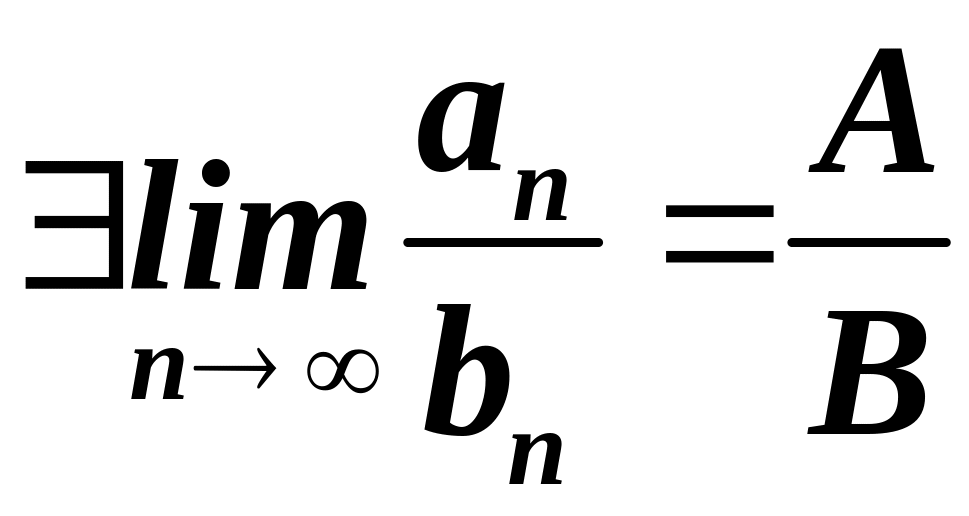Доведення.

Наслідок (із теореми 2). Сталий множник виноситься за знак границі, тобто, для : .

Арифметичні теореми легко розповсюджуються на випадок фіксованої кількості доданків (співмножників).

Теореми порівняння.

Теорема 1. Якщо послідовність - збіжна, причому , тоді і .

Доведення. (від супротивного)

Теорема 2. Якщо послідовності та - збіжні, причому , тоді .

Доведення.

Теорема 3 (Гур’єва). Якщо послідовності та - збіжні, причому , , і для усіх членів послідовності виконується умова . Тоді .

Теорема (Вейерштрасса). Будь-яка монотонна обмежена послідовність має границю (є збіжною).

Базуючись на теоремі Вейерштрасса доводиться існування чудової границі:

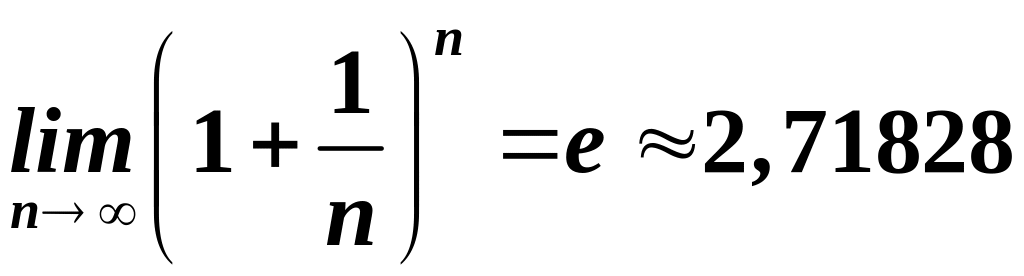(число Ейлера).

ТЕМА 13: Границя функції. Односторонні границі. Чудові границі. Розкриття невизначеностей. Неперервність функції. Класифікація точок розриву. Властивості функцій, неперервних на замкненому проміжку.

Границя функції. Односторонні границі.

Означення (за Гейне). Нехай функція визначена в деякому околі точки , за винятком, можливо, самої точки . Число називається границею функції в точці , якщо для будь-якої послідовності аргумента , відповідна послідовність значень функції . Позначається: .

Означення (за Коші). Число називається границею функції при , якщо для довільного додатного числа існує число таке, що із нерівності випливає нерівність .

Графічно:

Означення . Число ( )називається лівою (правою) границею функції в точці , якщо для будь-якої послідовності аргумента ( ), відповідна послідовність значень функції ( ). Позначається: ( ).

Графічно:

Теорема. Для існування границі функції в точці НІД, щоб існували і співпадали односторонні границі:

.

Для збіжних функцій (функцій, що мають границю), НМ та НВ справедливі усі раніше розглянуті для послідовностей властивості.

Розкриття невизначеностей.

При знаходженні границі функції рекомендуємо притримуватись наступної схеми:

1) зробити «прикидку», тобто підставити у функцію замість аргумента його граничне значення і виконати усі допустимі дії;

2) якщо немає невизначеності, то знайти границю застосуванням арифметичних теорем, властивостей НМ, НВ;

3) якщо є невизначеності, то потрібно спочатку позбутись її певними прийомами, а потім повернутись до пункту 1).

Приклад. Знайти .

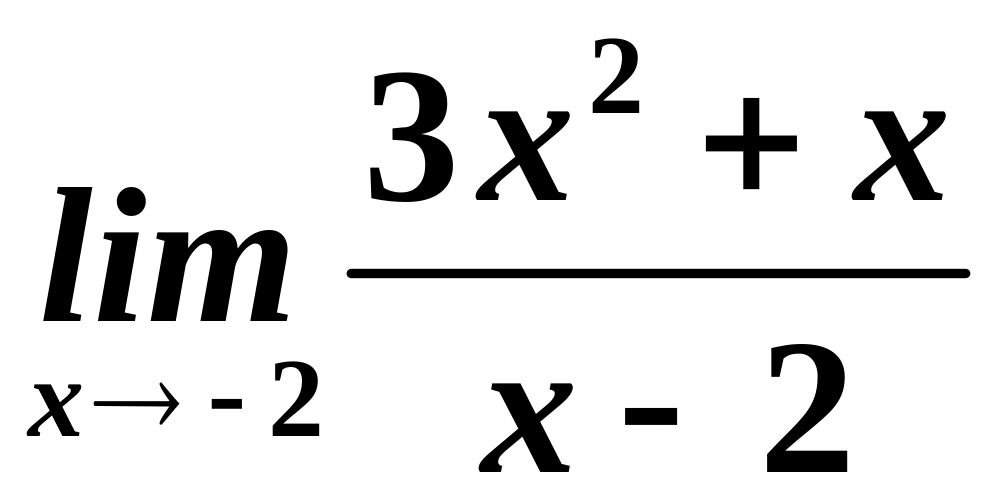Розв’язування.

Приклад. Знайти .

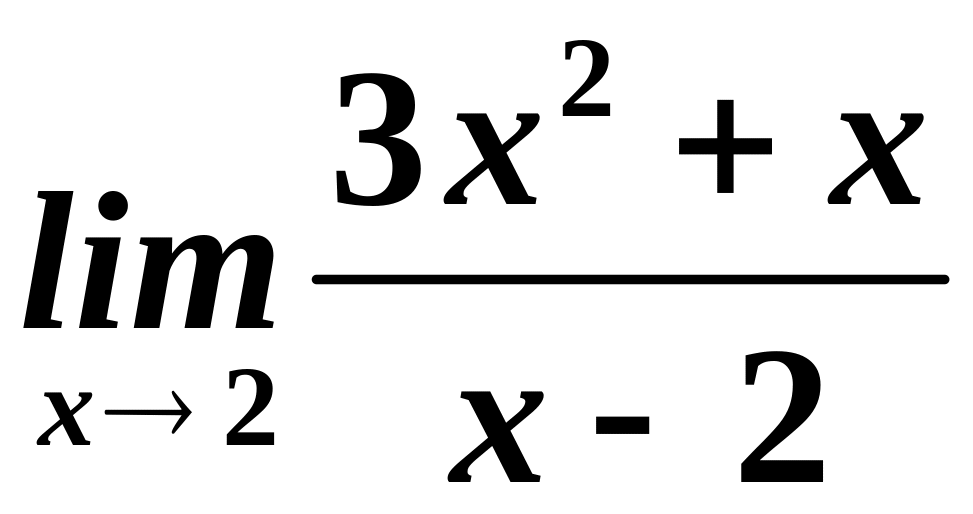Розв’язування.

Неосновні невизначеності алгебраїчними перетвореннями завжди можна звести до основних 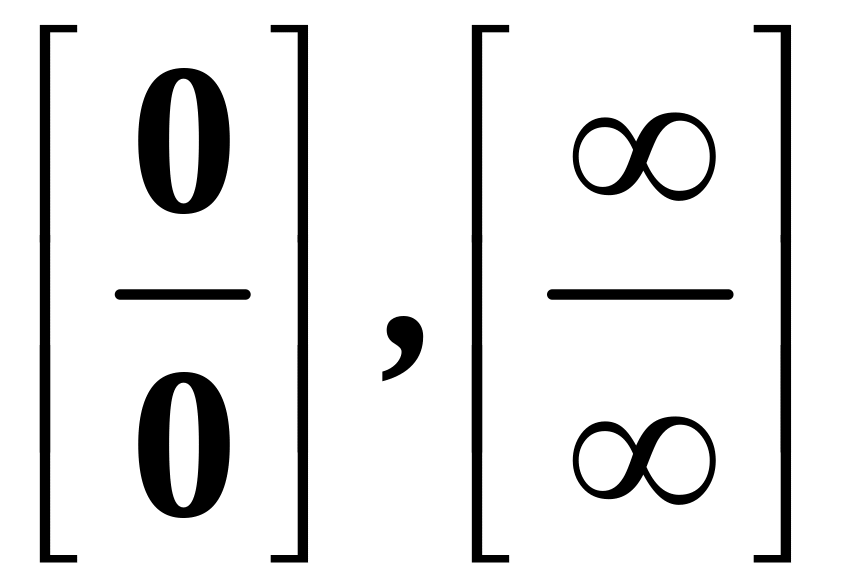, на розкритті яких зупинимось більш подробно.

Загальним правилом розкриття основних невизначеностей є рекомендація замінити НМ або НВ у чисельнику та знаменнику еквівалентними, більш простими величинами. Але це не завжди вдається зробити, тому розглянемо лише деякі найпростіші випадки.

Нехай знаходиться границя відношення двох многочленів 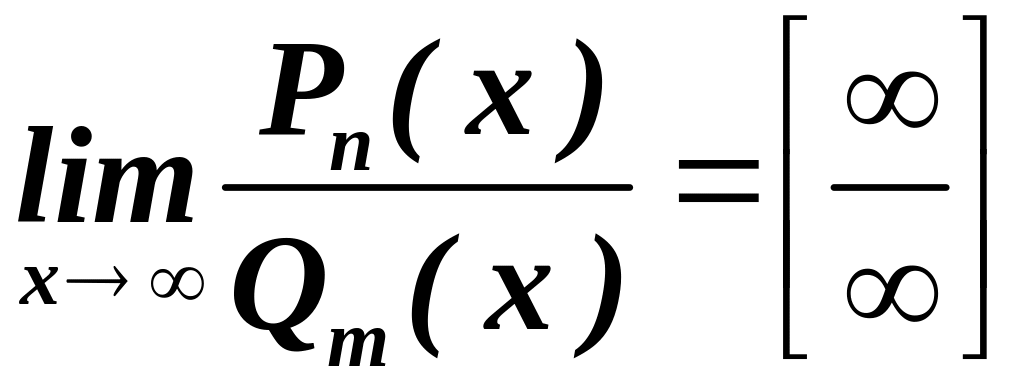. Для розкриття невизначеності замінимо многочлени в чисельнику та знаменнику еквівалентними їм старшими одночленами.

Приклад. Знайти .

Розв’язування. 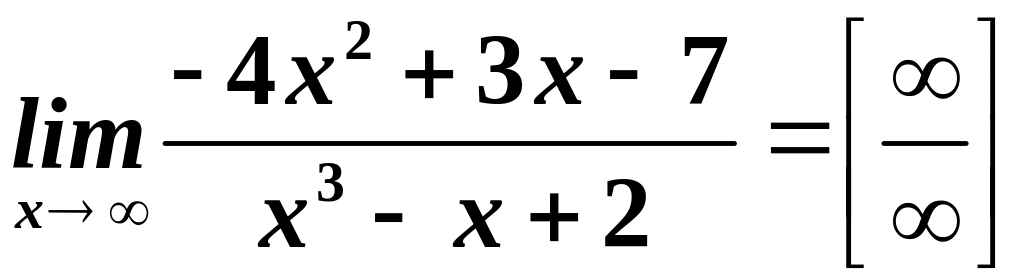при : - НВ, еквівалентна , а - НВ, еквівалентна , тому:

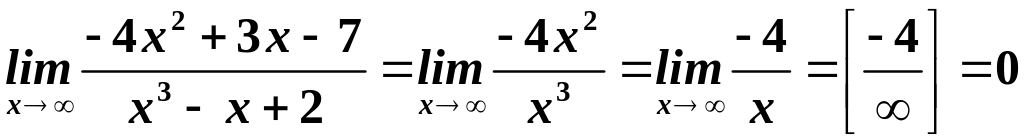за властивостями НМ, НВ.

Нехай знаходиться границя відношення двох многочленів 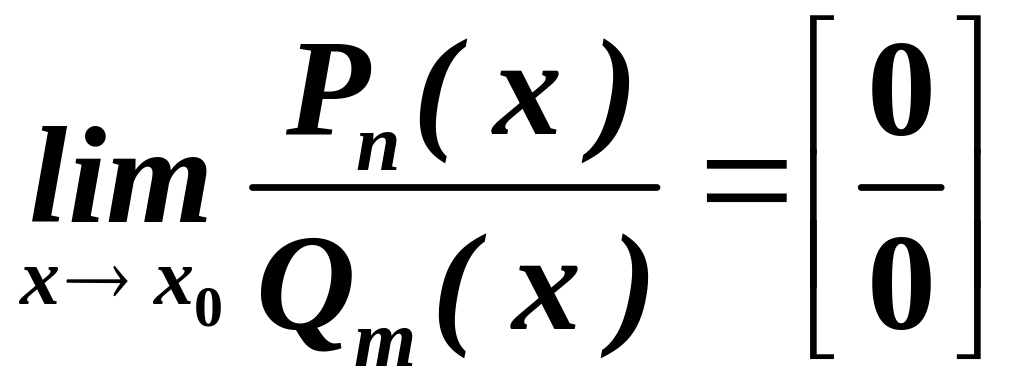. Для розкриття невизначеності поділимо многочлени в чисельнику та знаменнику на .

Приклад. Знайти .

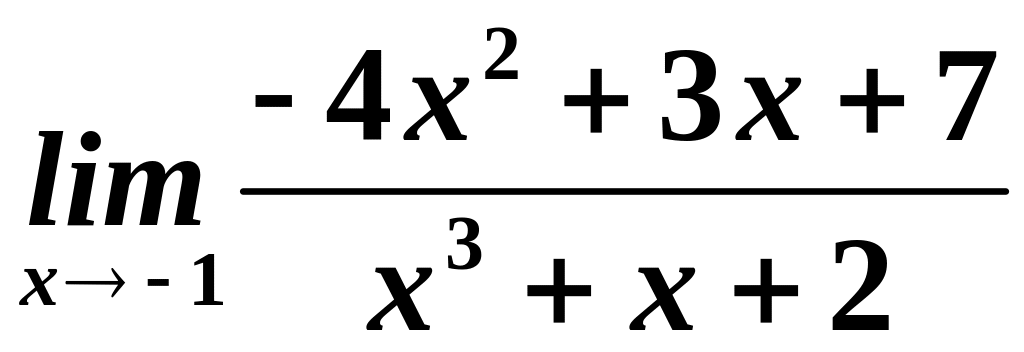Розв’язування.

Якщо невизначеність дають радикали, то потрібно спочатку позбутись ірраціональності.

Приклад. Знайти .

Розв’язування. При : 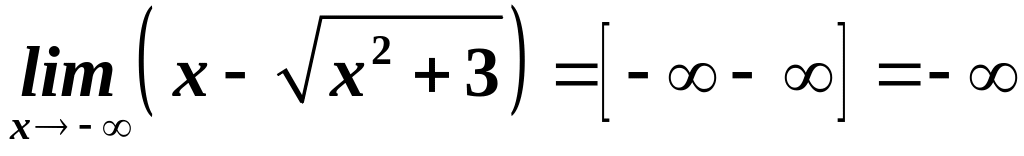- НВ за властивостями НВ.

При : 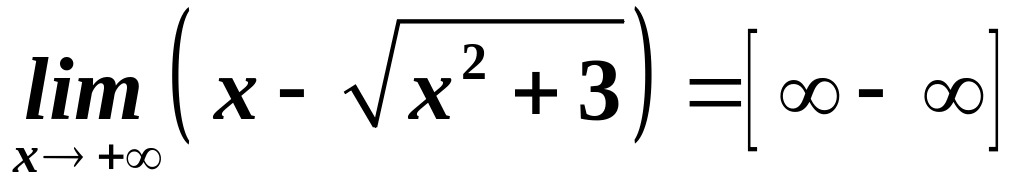- неосновна невизначеність із радикалами, тому домножимо і поділимо на «спряжений» вираз:

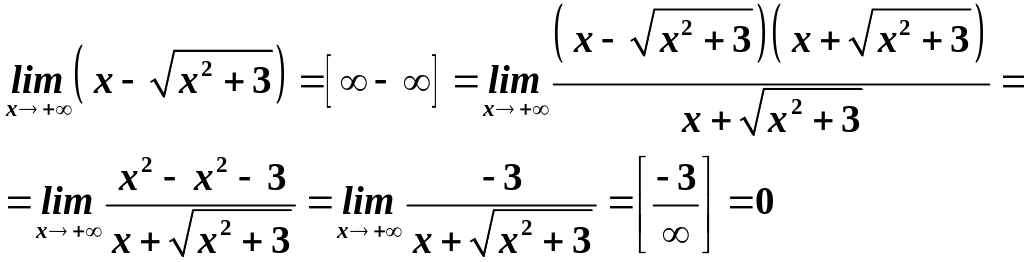
за властивостями НМ, НВ.

Для розкриття невизначеностей із тригонометричними функціями зводимо їх до чудової границі або наслідків з неї.

Чудова границя: 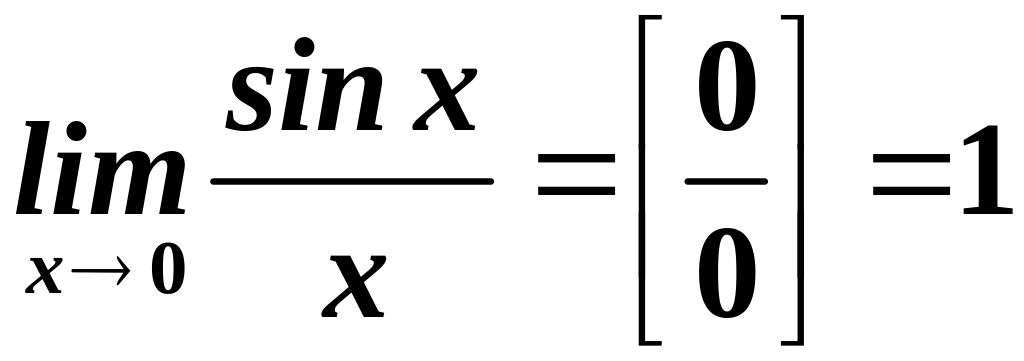. Наслідки:

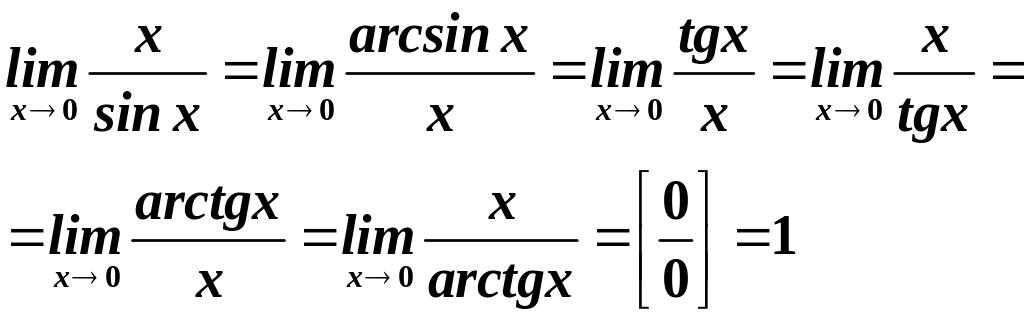
Іншими словами, при аргументі ( ), що прямує до нуля є НМ, які еквівалентні аргументу .

Приклад. Знайти .

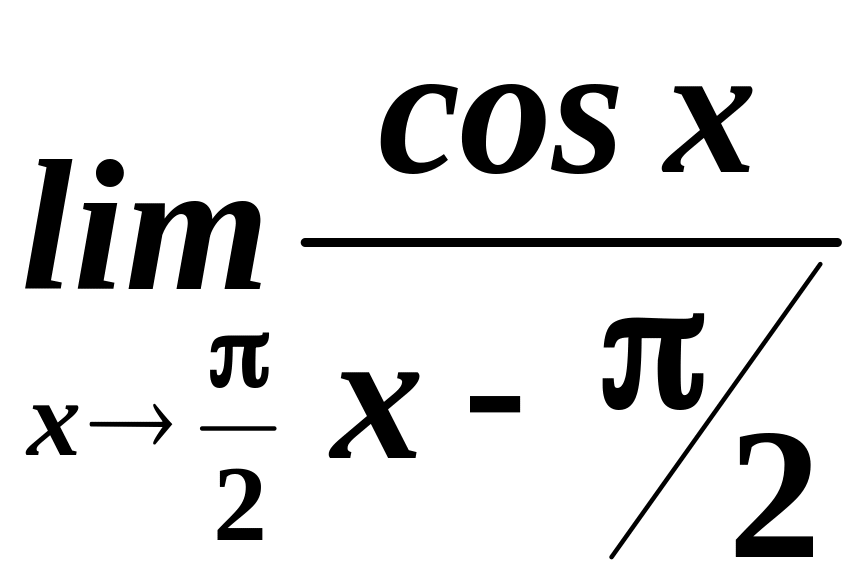Розв’язування.

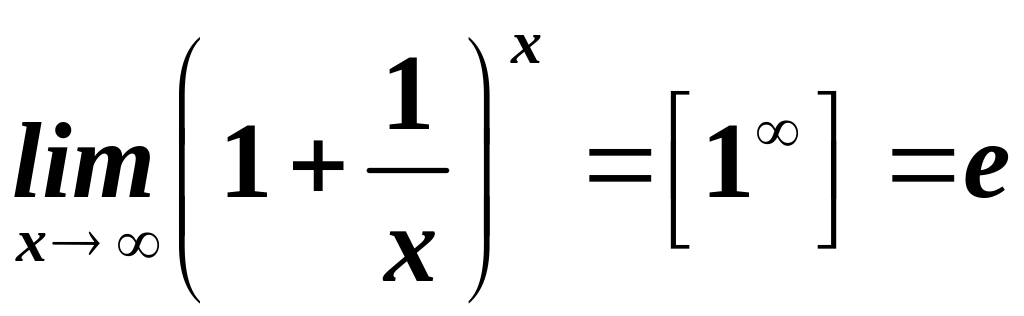Для розкриття невизначеності використовується чудова границя , або наслідок із неї – наступна формула:

.

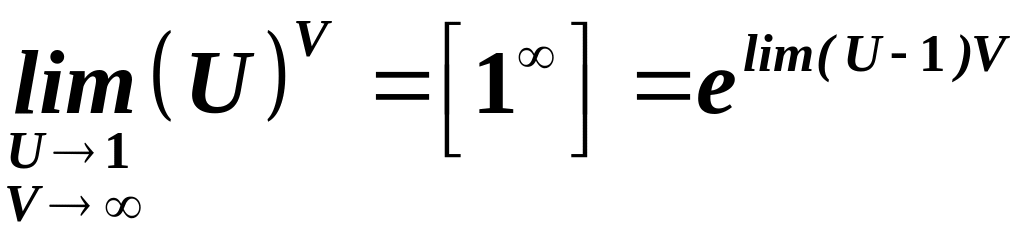Приклад. Знайти .

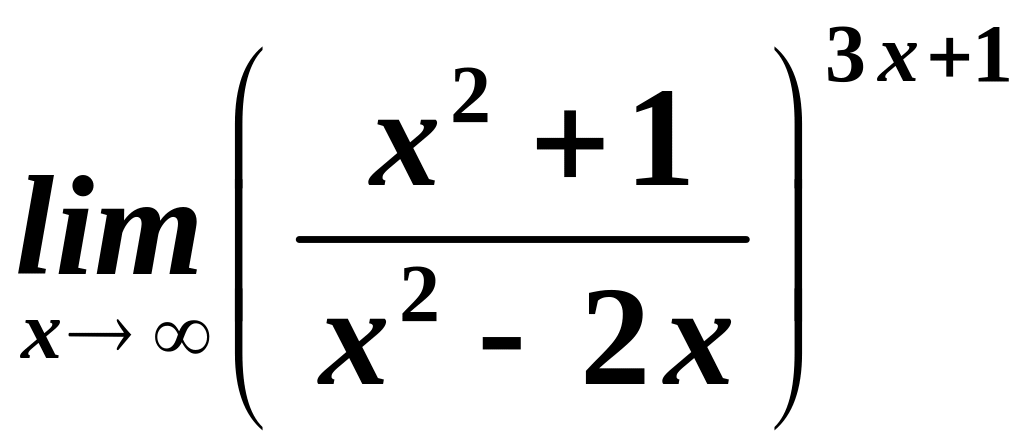Розв’язування.