28. Интегрирование методом замены переменной и по частям.
Интегрирование заменой переменной
Суть данного метода заключается в том, что в рассмотрение вводится новая переменная интегрирования или, что тоже самое, делается подстановка. После этого заданный в условии интеграл сводится либо к табличному интегралу, либо к нему сводящемуся.
Если
в неопределенном интеграле
сделать
подстановку
,
где функция
- функция с непрерывной первой производной,
то тогда
и
согласно свойству 6 неопределенного
интеграла имеем, что:
Эта формула называется формулой замены переменной в неопределенном интеграле.
После
нахождения интеграла по новой переменной
необходимо вернуться к первоначальной
переменной
.
В
некоторых случаях целесообразно делать
подстановку
,
тогда
Интегрирование по частям.
Если
функции u ( x ) и v ( x ) имеют непрерывные
первые производные и существует интеграл
v ( x ) du ( x ), то существует и интеграл
u ( x ) dv ( x ) и имеет место равенство:
u ( x ) dv ( x ) = u ( x ) • v ( x ) – v ( x ) du ( x )
или в более короткой форме:
u dv = u v – v du .
Обратите внимание, что интегрирование по частям и дифференциал произведения являются взаимно обратными операциями (проверьте!).
П р и м е р . Найти интеграл: ln x dx .
Р е ш е н и е. Предположим u = ln x и dv = dx, тогда du = dx/x и v = x. Используя формулу интегрирования по частям, получим:
29. Постановка задач линейного программирования. Пример ЗЛП. Каноническая форма ЗЛП.
Линейное программирование – одно из многих направлений математического программирования. Задачи математического программирования связаны с управлением различными производственными процессами:
с планированием выпуска наибольшего количества продукции при минимальных затратах;
с рациональным способом транспортировки продукции при минимальной стоимости транспортировки;
с повышением рентабельности производства;
со снижением себестоимости изготавливаемой продукции, и т.д.
Если рассматривать задачи математического программирования с точки зрения математика – то это задачи на условный экстремум, где необходимо найти максимум (минимум) некоторой функции нескольких переменных при условии, что на переменные наложена система ограничений. Термин “программирование” в таких задачах следует понимать как выбор программы, плана.
Общая постановка задачи линейного программирования
Задачу линейного программирования в общем виде можно сформулировать так:
найти такие значения переменных х1, х2,…,хn,
которые удовлетворяют систему ограничений
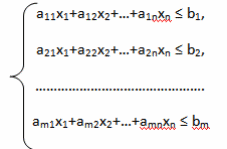и
преобразуют в экстремум (максимум или
минимум) линейную функцию
Z=c1x1+ c2x2+…+cnxn.
Функция Z называется целевой функцией. Каждый набор переменных, удовлетворяющий систему ограничений, называется допустимым решением или допустимым планом задачи линейного программирования. Совокупность всех допустимых решений называется областью допустимых решений (ОДР).
Пример задачи линейного программирования
Для изготовления двух видов изделий А и В на заводе используется три типа технологического оборудования. Во время изготовления единицы изделия А оборудование первого типа используется 16 часов, оборудование второго типа – 8 часов, оборудование третьего типа - 5 часов. Во время изготовления единицы изделия В оборудование разных типов используется соответственно 4, 7 и 9 часов. Во время изготовления всех изделий оборудование первого типа может быть в эксплуатации не больше 850 часов, оборудование второго типа – не больше 550 часов, а оборудование третьего типа – не больше 560 часов.
От реализации одного изделия вида А завод получает 480 рублей, а от реализации одного изделия вида В – 800 рублей прибыли. Требуется составить оптимальный план выпуска двух видов изделий А и В для получения наибольшей прибыли.
Математическая модель задачи
Построим математическую модель этой задачи. Пусть х – число изделий вида А, а у – число изделий вида В. Так как оборудование каждого типа может быть в эксплуатации не больше 850, 550 и 560 часов, то приходим к следующей системе ограничений:
16х+4у ≤ 850,
8х+7у ≤ 550,
5х+9у ≤ 560,
х ≥ 0,
у≥ 0.
Общая прибыль Z составит:
Z= 480x+800y.
Таким образом, построенная математическая модель нашей задачи состоит из системы неравенств, на множестве решений которой надо найти наибольшее значение целевой функции Z.
О методах решения задач линейного программирования – в следующих статьях. Это не так уж и сложно – решать такие задачи. Есть определенные алгоритмы, было бы только желание.
Каноническая задача ЛП.
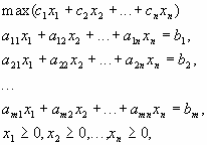
или, в матричной записи,
Основные вычислительные схемы решения задач ЛП разработаны именно для канонической задачи.