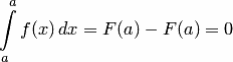22. Функции многих переменных. Геометрический смысл функции двух переменных.

Мы определяли функцию одного вещественного аргумента как отображение f : D → R некото-

рого подмножества D ⊂ R действительных чисел в действительные числа. Аналогичное опреде-

ление можно дать и в случае нескольких аргументов:

Определение 1. Пусть D ⊂ Rⁿ — подмножество множества n-мерного арифметического про-

странства. Отображение f : D → R называется функцией n вещественных аргументов (x1,... ,xn).

При этом множество D называется областью определения функции f, а множество

V = { u ∈ Rⁿ| u = f(x) }

— областью допустимых значений. Графиком функции u = f(x) называется множество

{ (x1,... ,xn,u) | u = f(x1,... ,xn) } ⊂ ^Rn+1.

Это определение, однако, является слишком общим, широким, и в следующем параграфе мы

уточним, какие области определения допускаются нами к рассмотрению. Чтобы это сделать, нам

понадобятся элементарные сведения из топологии пространств Rⁿ.

23. Наибольшее и наименьшее значение функции двух переменных.

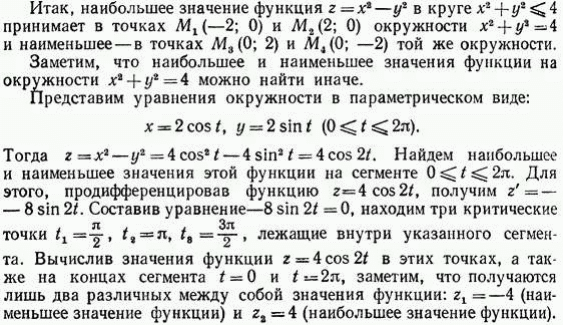
24. Первообразная, неопределенный интеграл.

Первообразной функцией для функции f(x) называется такая функция F(х), производная которой равна данной функции

F'(x) = f(x).

Обозначение

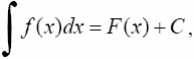
где F'(x) = f(x). Функция f(x) называется подынтегральной функцией, а выражение f(x)dx - подынтегральным выражением.

Свойства неопределенного интеграла

1°. Производная неопределенного интеграла равна подынтегральной функции; дифференциал от неопределенного интеграла равен подынтегральному выражению, т.е.

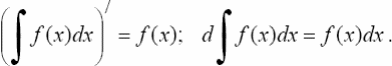
2°. Неопределенный интеграл от дифференциала некоторой функции равен сумме этой функции и произвольной постоянной, т.е.

3°. Постоянный множитель можно вынести из под знака интеграла, т.е. если k = const ≠ 0, то

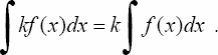
4° . Неопределенный интеграл от алгебраической суммы двух функций равен алгебраической сумме интегралов от этих функций в отдельности.

25. Таблица интегралов

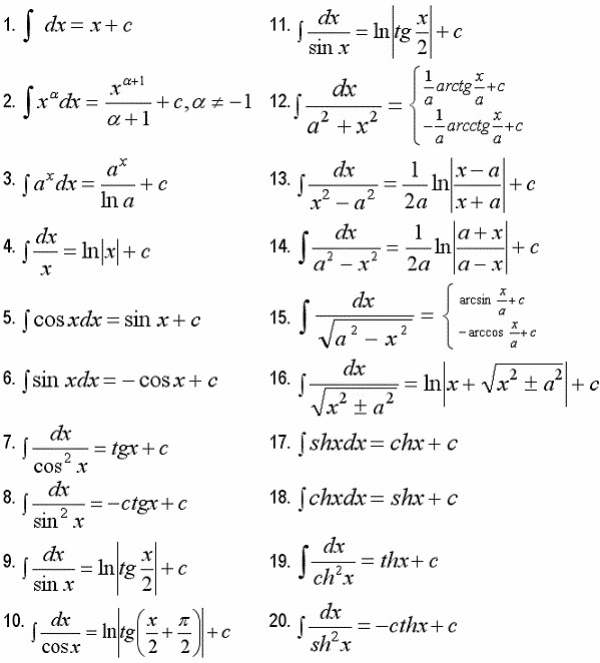
26. Свойства интегралов

Вычисление многих интегралов сводится к табличным, если использовать свойства неопределенных интегралов, вытекающие из соответствующих свойств дифференциалов. Рассмотрим некоторые из них:

а) Постоянный множитель можно вынести за знак неопределенного интеграла:

Доказательство. Продифференцировав правую часть равенства, получаем:

Таким образом, дифференциал правой части доказываемой формулы равен подынтегральному выражению левой части, а это и означает справедливость формулы (1).

б) Если существуют интегралы и , то не определенный интеграл суммы f₁(x)+f₂(x) равен сумме неопределенных интегралов от этих функций:

Доказательство. Продифференцируем правую часть равенства (2):

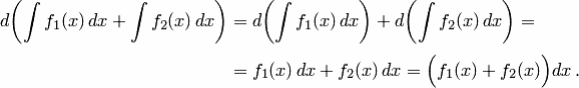
Мы получили подынтегральное выражение неопределенного интеграла, стоящего в левой части равенства (2), откуда и следует справедливость утверждения.

Свойства определенного интеграла

Так как определенный интеграл равен разности значений первообразной, та его свойства выводятся из свойств неопределенного интеграла.

а) Если существует и — любое число, то

Доказательство. Из соответствующего свойства неопределенных интегралов следует, что если — первообразная для , то первообразная для . Значит,

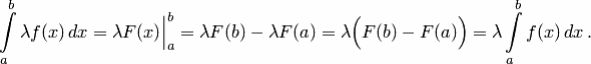
б) Если функции и имеют первообразные на отрезке [a;b], то

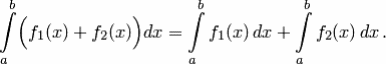
Доказательство. Из соответствующего свойства неопределенных интегралов следует, что если — первообразная для , а - первообразная для на отрезке [a;b], то F₁(x)+F₂(x) — первообразная для f₁(x)+f₂(x). Значит,

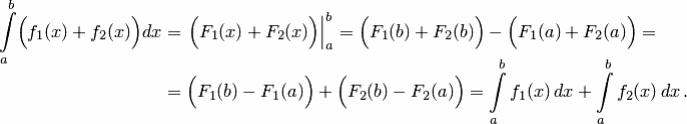
в) Если функция f(x) имеет первообразную на отрезке [a;b] и если a<c<b, то (аддитивное свойство определенного интеграла)

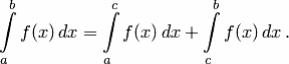
Доказательство. Пусть F(x) — первообразная для f(x). Тогда

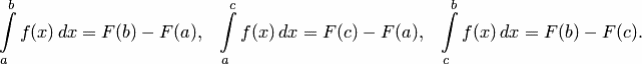
Но . Значит,

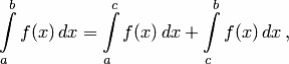
что и требовалось доказать.

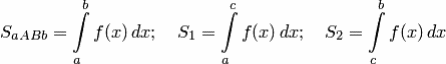. Тогда

г) Если функция y=f(x) имеет первообразную на отрезке [a;b], то справедливо равенство

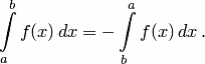
Доказательство. Пусть F(x) — первообразная для f(x). Тогда

Но F(b)-F(a)=-(F(a)-F(b)), откуда и следует доказываемое утверждение.

д) 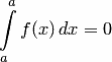Доказательство: