2.4. Похибки арифметичних операцій

Похибки суми і різниці. Розглянемо точні числа і їх наближені значення Нехай 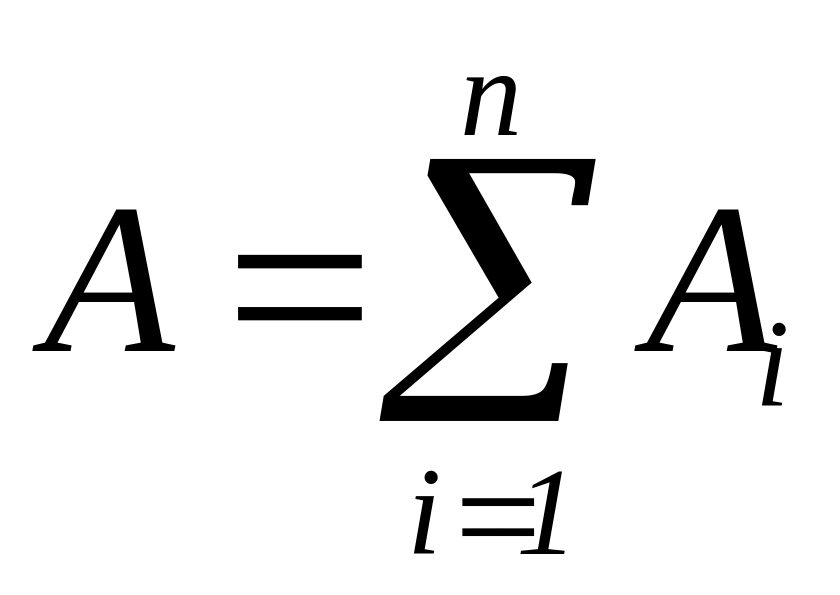– сума всіх точних чисел; 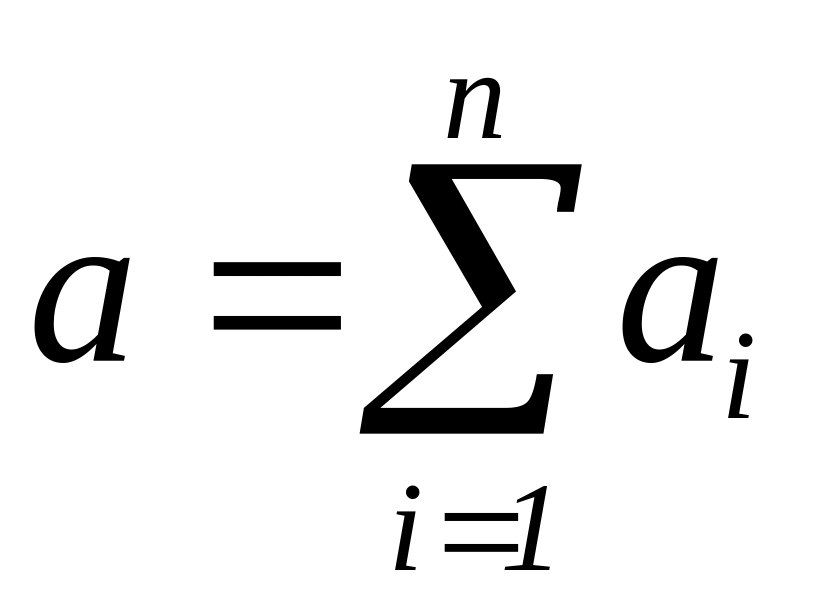– сума їх наближених значень. Поставимо задачу: при відомих абсолютних похибках всіх наближених чисел оцінити абсолютну похибку їх суми а..

Запишемо різницю Перейшовши до абсолютних величин правої і лівої частин цього відношення і використовуючи властивість абсолютних величин, отримаємо Відповідно,

(2.11)

і як абсолютну похибку наближеного числа а, тобто суми наближених чисел можна прийняти суму абсолютних похибок доданків:

(2.12)

З останньої формули випливає, що абсолютна похибка алгебраїчної суми, в загальному випадку, не повинна бути менше абсолютної похибки найбільш неточного з доданків. Тому, щоб не виконувати зайвих розрахунків, не потрібно зберігати зайві знаки і в точніших доданках.

Зауваження. При великій кількості доданків (n>10) оцінка абсолютної похибки суми за формулою (2.12) виявляється дуже завищеною, оскільки завжди виконується частинна компенсація похибок різних знаків. Якщо всі доданки округлені до m–го десяткового розряду, тобто їх похибки оцінюються величиною , то статична оцінка абсолютної похибки суми обчислюється за формулою

Зауважимо, що під час віднімання близьких чисел часто виникає стан, що називається втратою точності [4]. Нехай х>0, y>0 і , тоді .

Таким чином, якщо числа х і y мало відрізняються одне від одного, то навіть при малих похибках і величина відносної похибки різниці може виявитись значною.

Приклад 1. Нехай х=5,125, y=5,135 тут =0,0005, =0,0005, %. Відносна похибка різниці складає

%.

Очевидно, що в результаті ділення двох наближених чисел може виникнути значна втрата точності. Щоб цього не допустити, слід спробувати так перетворити обчислювальну схему, щоб малі різниці величин обраховувались безпосередньо.

Приклад 2. Знайти різницю та оцінити відносну похибку результату.

Нехай ; ; ; . Тоді ; звідки %.

Однак, змінивши обчислювальну схему, можна отримати значно кращу оцінку відносної похибки:

%.

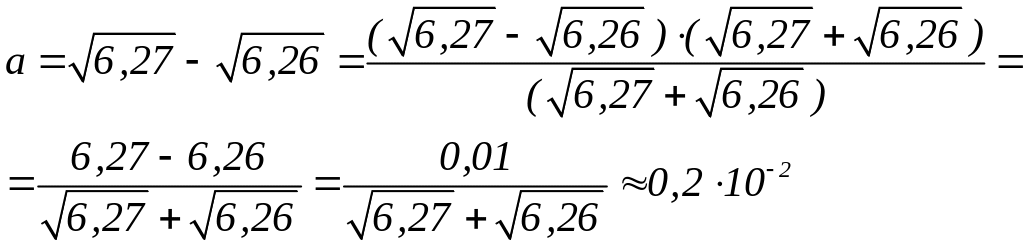
Таким чином, при обчисленні з тими ж чотирма вірними знаками і ми отримали значно кращий результат в розумінні відносної похибки.

Похибка добутку. Розглянемо два точних числа А₁ і А₂ та їх наближені значення а₁ і а₂. Нехай А=А₁А₂ і а=а₁а₂. Поставимо задачу: оцінити відносну похибку добутку , якщо відносні похибки чисел а₁ і а₂ дорівнюють і відповідно.

Представимо А₁ і А₂ у вигляді , де невідомі Δ₁ і Δ₂ задовольняють нерівності

(2.13)

Перемноживши праві і ліві частини цих співвідношень, отримаємо Перейшовши до абсолютних величин правої і лівої частин цього співвідношення і використовуючи властивості абсолютних величин, отримаємо

Відкинемо останній доданок правої частини, оскільки, він дуже малий і поділимо праву і ліву частину нерівності на . Тоді, враховуючи (2.13), маємо

З отриманого співвідношення випливає, що як відносну похибку добутку а=а₁а₂ можна прийняти суму відносних похибок співмножників:

= + . (2.14)

Нерівність (2.14) легко поширюється на добуток декількох співмножників так, що якщо А=А₁А₂..А_n і а=а₁а₂..а_n, то можна прийняти, що

= + +…+ ... (2.15)

В тому випадку, коли всі співмножники, крім одного, є точними числами, з формули (2.15) випливає, що відносна похибка добутку збігається з відносною похибкою наближеного співмножника. Таким чином, якщо наближеним числом є лише значення множника а_i, то

= . (2.16)

Зауваження. При множенні наближеного числа а на точний співмножник відносна похибка добутку дорівнює відносній похибці наближеного числа а, а абсолютна похибка у разів більше абсолютної похибки наближеного числа.

Число вірних знаків добутку. Нехай даний добуток має співмножників ( ) а=а₁а₂..а_к, де . Кожний із співмножників містить не менше ніж n вірних цифр ( ).

Нехай кожний із співмножників має вигляд

(i=1, 2, …, k), (2.17)

де – перші значущі цифри наближених співмножників, записаних у десятковій системі числення.

Для відносної похибки наближеного числа, що має n вірних знаків, використовуємо формулу

тоді відносна похибка добутку k наближених чисел, кожне з яких має n вірних значущих цифр, дорівнює

(2.18)

Враховуючи, що число співмножників не більше 10 ( ), отримаємо 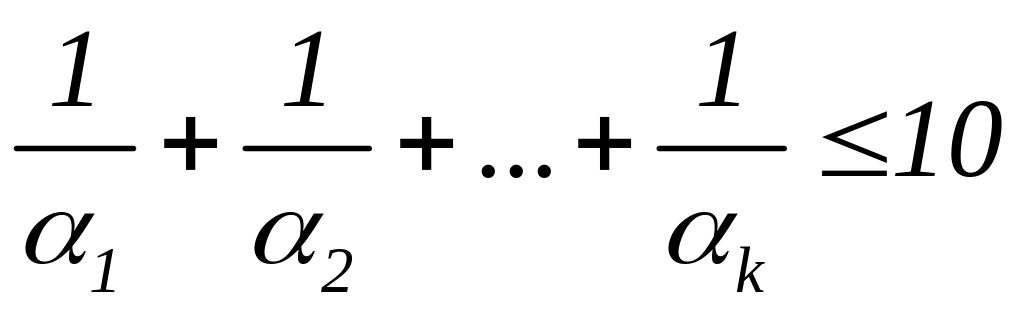і, отже, .

Таким чином, якщо всі співмножники мають n вірних значущих цифр і число співмножників не більше десяти, то число вірних знаків добутку на одну або дві одиниці менше ніж в n. У тому випадку, коли співмножники мають різну точність, під n варто розуміти число вірних знаків найменш точного із співмножників.

Зауваження. При великому числі співмножників (k>10) зручно користуватися статистичною оцінкою, яка враховує часткову компенсацію похибки різних знаків. Якщо всі числа (i= 1, 2, …, k) мають приблизно однакову відносну похибку , то відносна похибка добутку приймається рівною [4]

. (2.19)

Похибка частки. Розглянемо точні числа А₁, А₂ та їх наближені значення а₁, а₂ з абсолютними похибками . Поставимо задачу: оцінити відносну похибку наближеного значення частки а=а₁/а₂ для точного значення А=А₁/А₂. Нехай , . Точні значення А₁ і А₂ представимо у вигляді

, , (2.20)

де невідомі і задовольняють нерівностям

, . (2.21)

Розглянемо тепер різницю 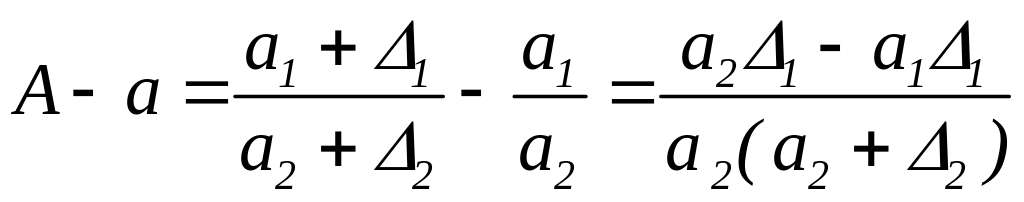. Поділивши праву і ліву частини на а, розглянемо їх абсолютні величини: 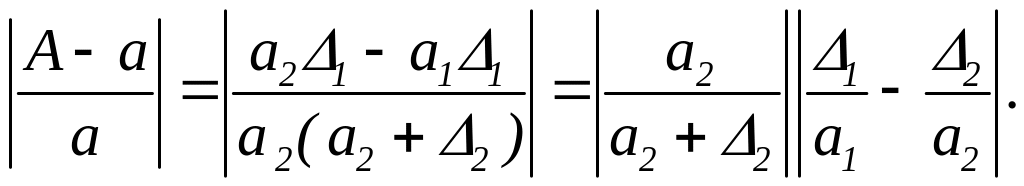Враховуючи, що мале порівняно з , наближено представимо, що Тоді, використовуючи властивості абсолютних величин і нерівність (2.21), отримаємо

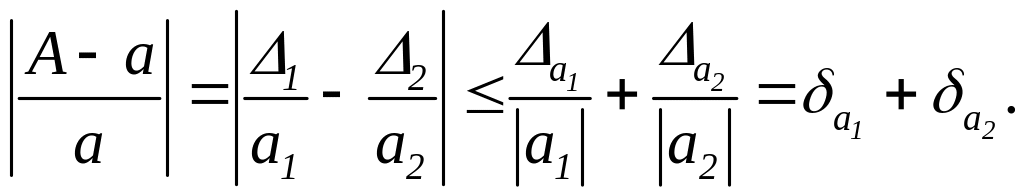
Таким чином, за відносну похибку частки можна прийняти суму відносних похибок діленого і дільника:

. (2.22)

Число вірних знаків частки. Нехай наближені числа

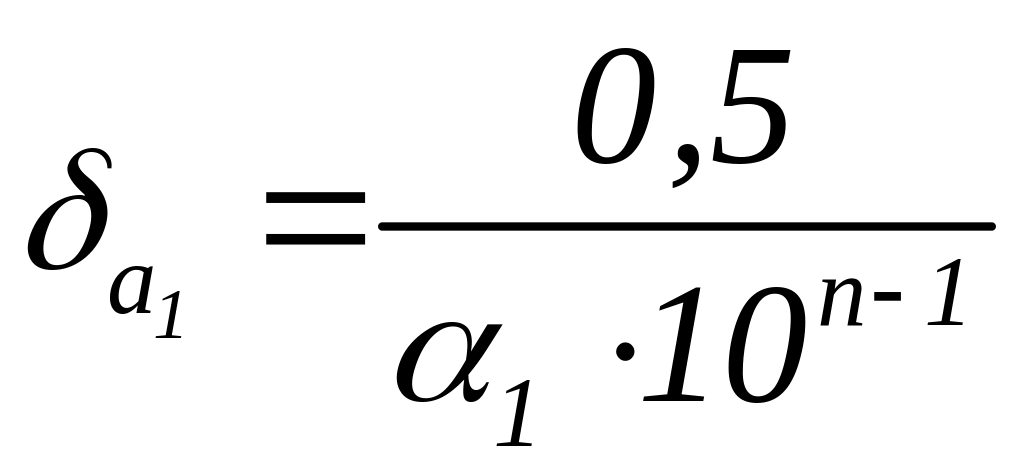
мають по n вірних значущих цифр. Тоді, використовуючи рівності 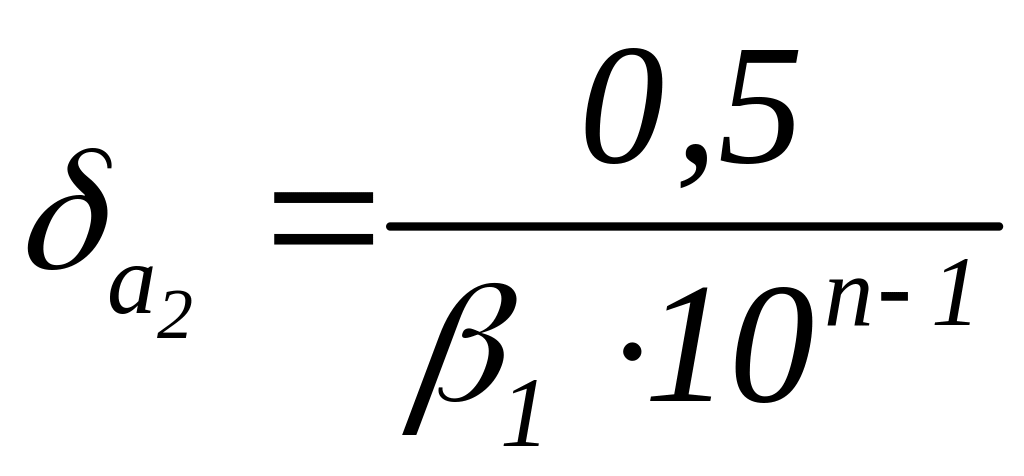, знайдемо відносну похибку частки :

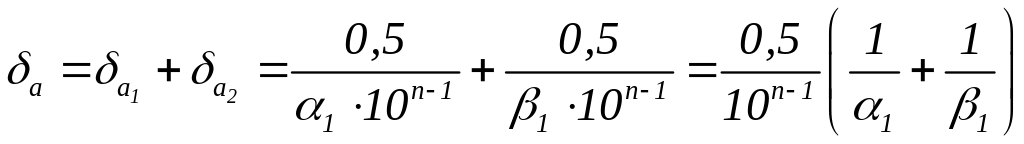_. (2.23)

Відповідно, якщо і , то частка має вірну значущу цифру. Якщо ж і то частка може мати вірних значущих цифр.

П охибки степеня і кореня. Розглянемо наближене число , яке має відносну похибку . Нехай треба оцінити похибку степеня . Очевидно, що Отже, відносна похибка добутку може

бути знайдена за формулою

(2.24)

В практичних розрахунках при піднесенні до степеня наближеного числа в результаті залишають стільки значущих цифр, скільки їх містило наближене число.

Відносна похибка числа в m разів менша за відносну похибку числа a₁: .

В практичних розрахунках під час обчислення кореня з наближеного числа в результаті залишають стільки значущих цифр, скільки їх містило наближене число.