1.3. Поняття стійкості та коректності

Похибки у вхідних даних задачі – неусувні. Дослідник не може їх зменшити, але повинен знати як вони впливають на точність кінцевого результату. Одні задачі мають похибку результату одного порядку з похибками вхідних даних, в інших задачах похибка результату може на кілька порядків перевищувати похибку вхідних даних. Чутливість задачі до неточностей у вхідних даних характеризується поняттям стійкості.

Задача є стійкою за вхідними даними, якщо її розв'язок безперервно залежить від вхідних даних, тобто малому прирісту вхідної величини відповідає малий приріст шуканого розв'язку. Іншими сло­вами, малі похибки вхідних даних спричиняють малі похибки розв'язку за­дачі. Якщо ця умова не виконується – задача є нестійкою за вхідними даними. Це означає, що навіть незначні похибки вхідних даних можуть привести до як завгодно великих похибок розв'язку, тобто розв'я­зок може бути дуже викривлений. Тому застосовувати безпосередньо до таких задач чисельні методи не можна, оскільки похибки округлень при застосуванні методу будуть катастрофічно нагромаджуватись у ході обчи­слень.

Наведемо приклад нестійкої задачі, який належить Уілкінсону [1]. Коренями многочлена

(1.3)

є числа . Нехай один з його коренів обчислено з незначною похи­бкою, наприклад, коефіцієнт –210 при х¹⁹ замінено на коефіцієнт –210+2^–23 . Тоді дещо змінений многочлен має такі округ­лені до двох десяткових (після коми) знаків корені:

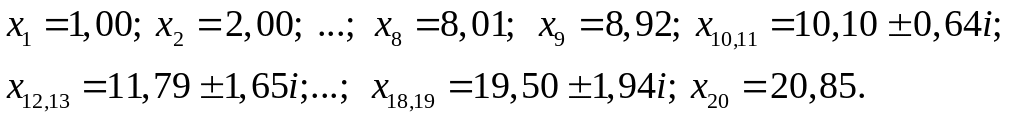
Незначна похибка в коефіцієнті –210 даного многочлена викликала суттєво інші значення коренів (десять з них стали комплексними). Причиною цього є нестійкість задачі, оскільки корені обчислювали з точністю до 11 значущих цифр і похибка округлень незначна.

Іноді під час розв'язування стійкої за вхідними даними задачі не­стій­ким може бути метод її розв'язування. Нехай треба обчислити інтеграли [1]

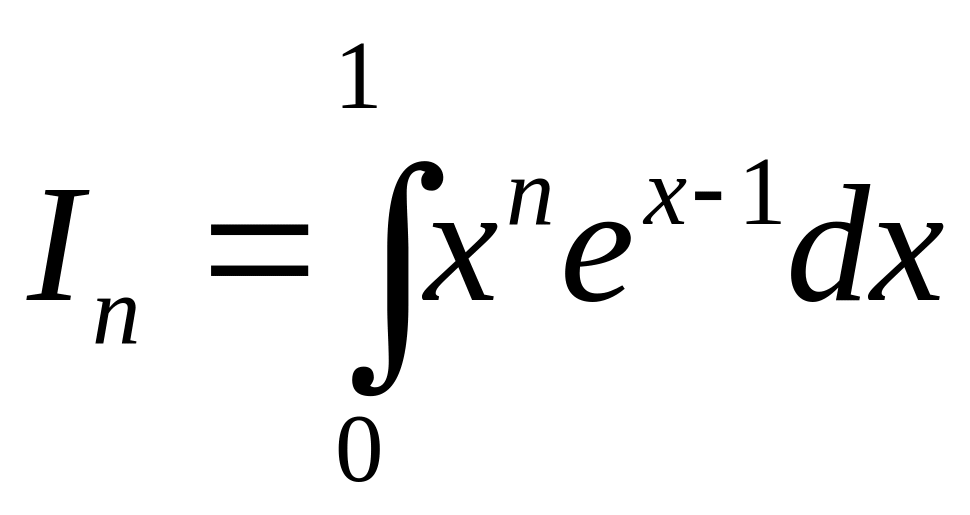, (1.4)

Інтегруючи за частинами, маємо

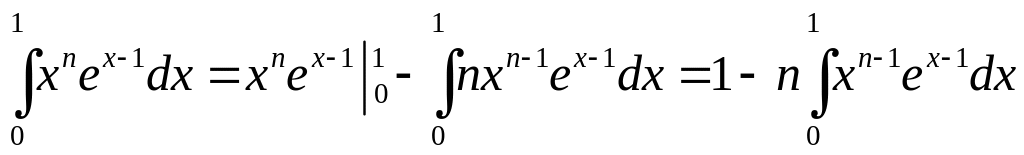
Звідси дістанемо

Використавши рекурентне співвідношення, обчислимо перші дев'ять інтегралів І₁ = 0,367879, І₂ = 0,264242, І₃ = 0,207274, І₄ = 0,170904, I₅ = 0,145480, І₆ = 0,127120, І₇ = 0,110160, І₈ = 0,118720, І₉ = 0,0684800.

Значення інтеграла І₉ помилкове, оскільки підінтегральна функція в усіх точках відрізка [0; 1] невід'ємна. Помилка зумовлена похибкою округлення значення І₁ до шести значущих цифр. Ця похибка наближено дорівнює . При обчисленні І₁ вона множиться на –3 і т.д. Похибка в І₉ дорівнює . Вона спотворила істинне значення І₉, яке з трьома значущими цифрами дорівнює 0,0916.

Введемо тепер поняття коректності задачі. Задача є коректно поставленою, якщо для будь–яких вхі­дних даних з деякого класу існує єдиний і стійкий за вхідними даними її розв'язок [1]. Наведена вище задача обчислення коренів многочлена (1.3) є не­коректно поставленою, а обчислення інтегралів (1.4) – коректно поставленою задачею. Прикладом некоректно поставленої задачі є також задача чисельного диференціювання функцій.

Для розв'язування некоректно поставлених задач застосовувати класичні чисельні методи не слід, оскільки похибки округлень при розра­хунках можуть катастрофічно зростати і призвести до результату, далекого від шуканого розв'язку. Для розв'язування некоректно поставлених задач використовують так звані методи регуляризації, які замінюють дану задачу коректно поставленою [1, 12].