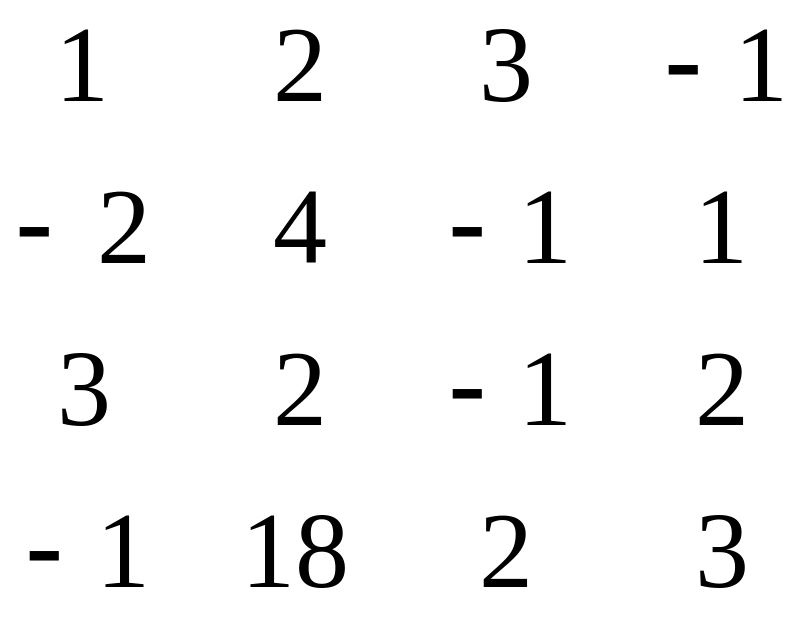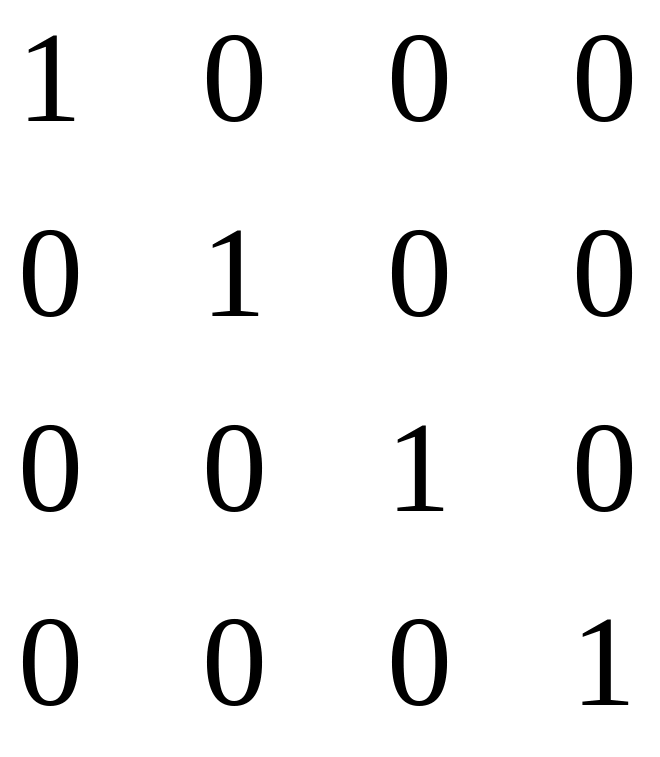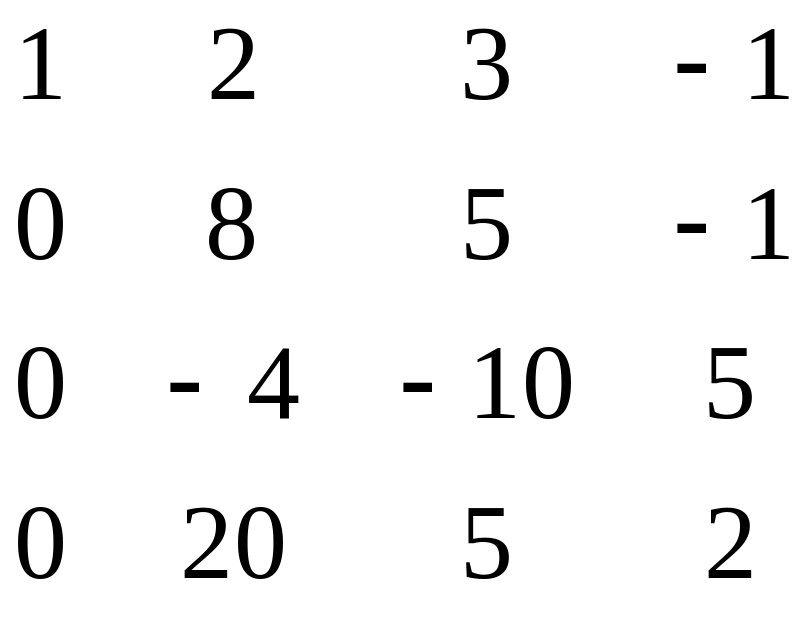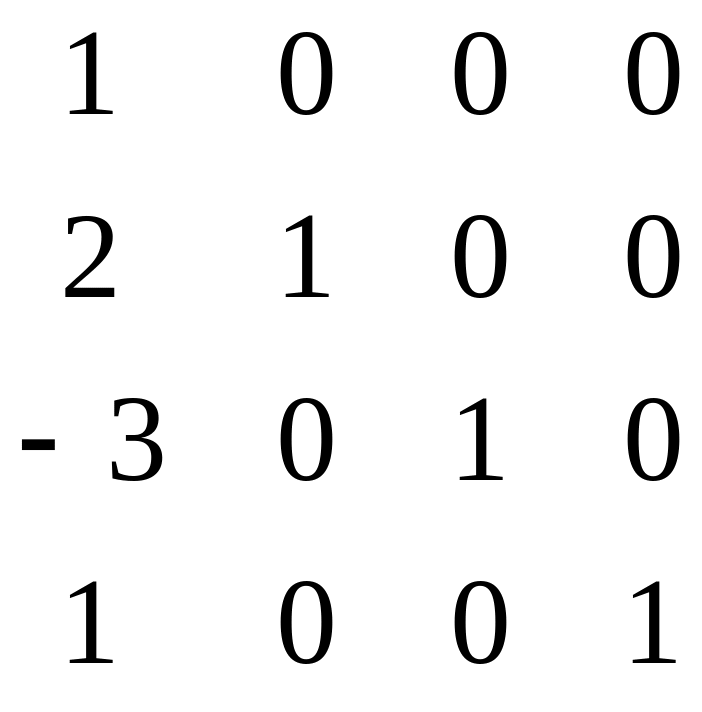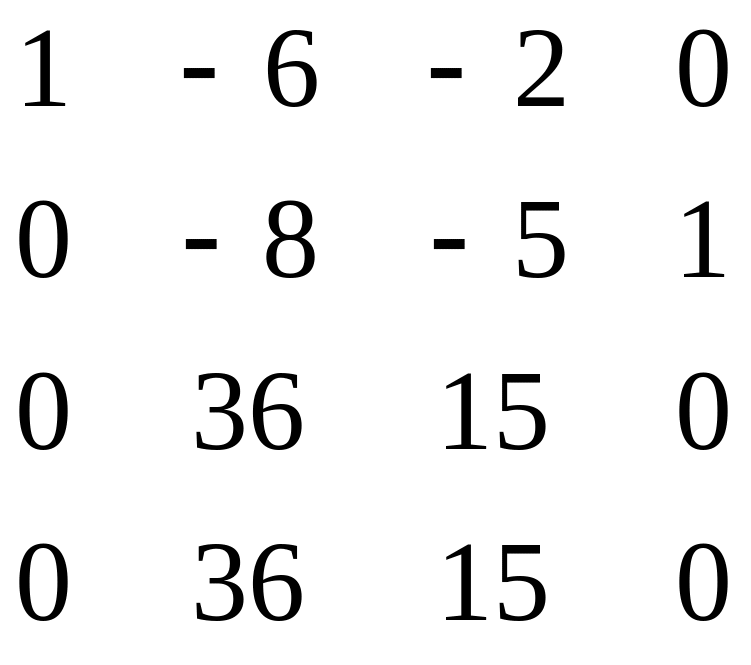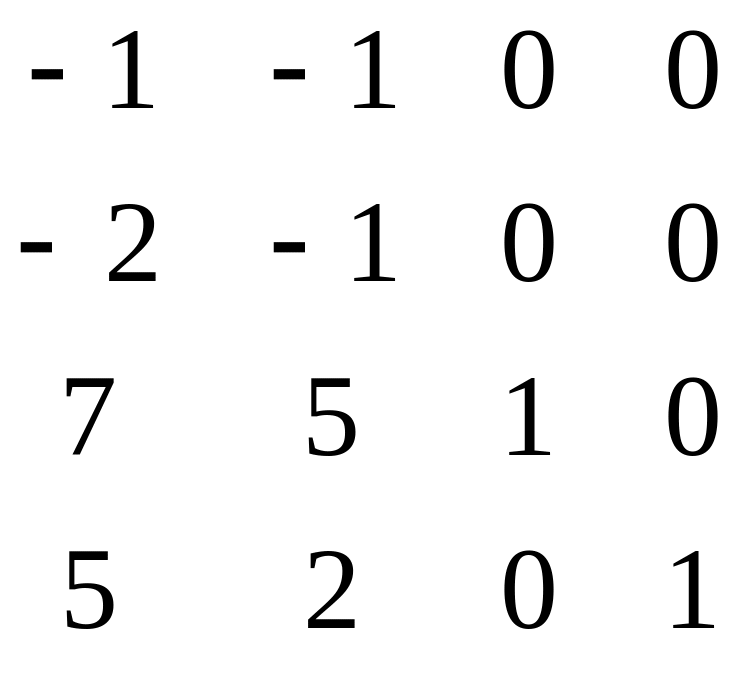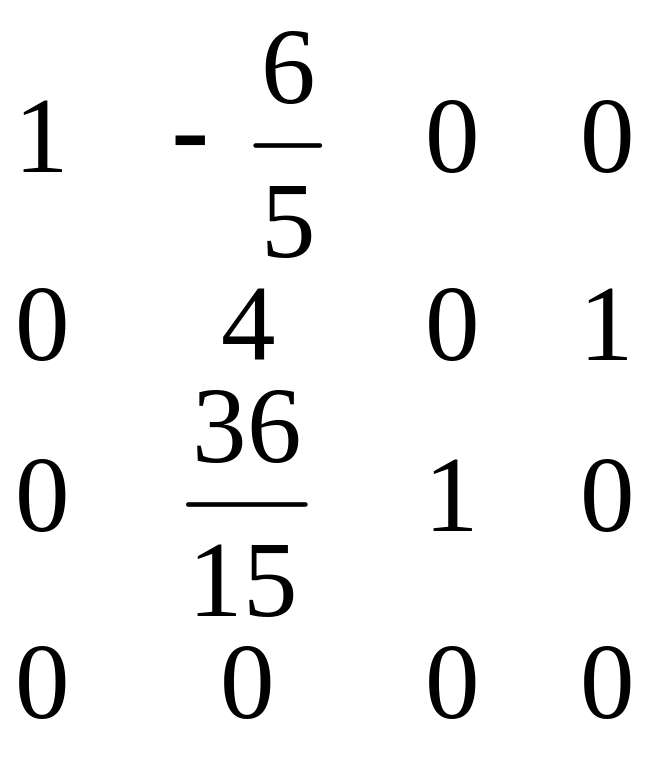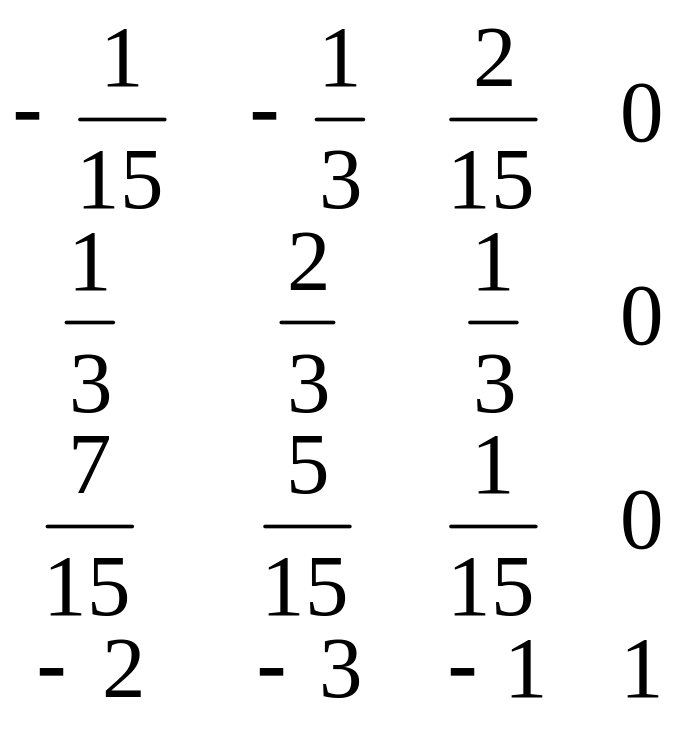4.4.4. Метод Гаусса–Жордана

Нехай є система т лінійних алгебраїчних рівнянь з п невідомими (n та m – довільні). Метод послідовного виключення невідомих з усіх рівнянь системи, крім одного, називають методом Гаусс­а–Жордана. Цей метод також є деякою модифікацією розгляну­того методу Гаусса [3].

Нехай у вихідній системі a_ij  0 (називатимемо його далі розв'язувальним елементом. Виключимо з усіх рівнянь сис­теми, крім i–го, невідоме x_j. Для цього виконаємо такі операції:

1) поділимо i–те рівняння на а_ij :

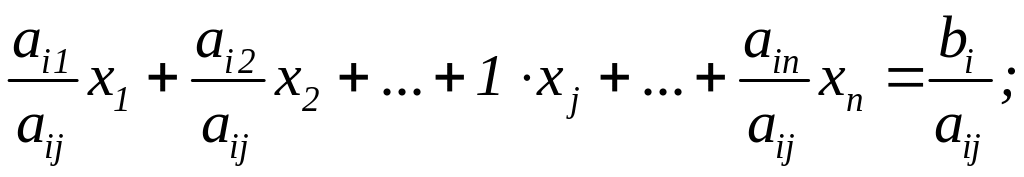(4.23)

2) рівняння (4.23) помножимо на коефіцієнт а_kj (k = 1, 2, ..., i– 1, i+1, ..., т):

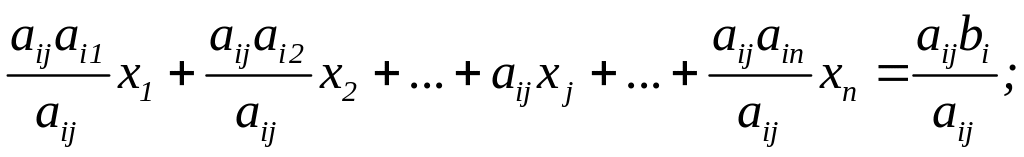(4.24)

3) рівняння (4.24) віднімемо від k–го рівняння вихідної системи:

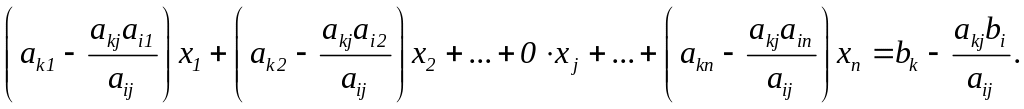Введемо позначення:

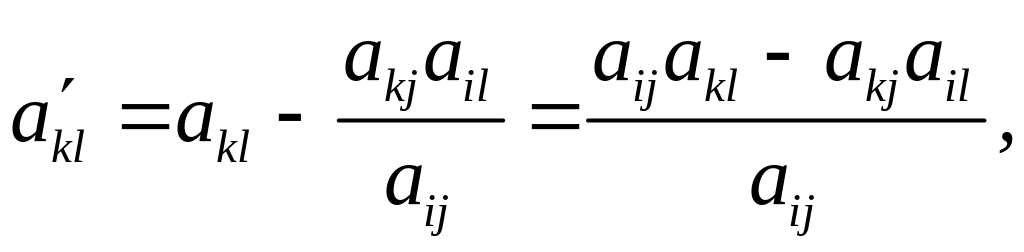l=1, 2, …, n;

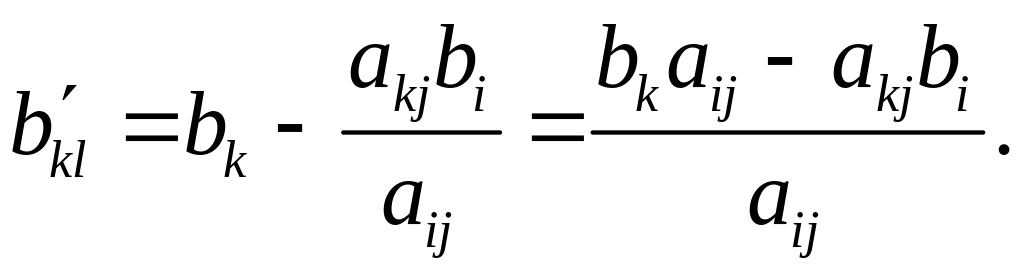
Тоді

(k= 1, 2, …, i–1, i+1, …, m). (4.25)

Отже, в результаті перетворень 1) – 3) вихідну систему зведено до еквівалентної системи

,

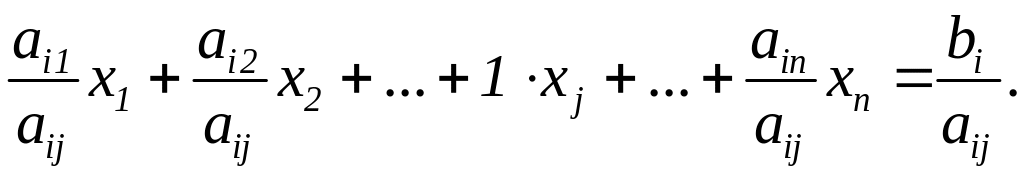(4.26)

Зведення вихідної системи до системи (4.26) називають кроком послідовних виключень Гаусса – Жордана. Усі обчислення зручніше виконувати тоді, коли задану та всі наступні сис­теми записувати у вигляді таблиць.

Запишемо таблиці, що відповідають вихідній системі та системі (4.26) (відповідно табл. 4.4 і 4.5).

У табл. 4.4 розв'язувальний елемент а_ij візьмемо в рамку; i–й рядок та j–й стовпець називатимемо відповідно разв'язувальним рядком та разв'язувальним стовпцем.

Таблиця 4.4

Таблиця 4.5

x1	x2	…	xj	…	xn	bi
а11	a12	…	a1j	…	a1n	b1
а21	a22	…	a2j	…	a2n	b2
…	…	…	…	…	…	…
ai1	ai2	…	a ij	…	ain	bi
…	…	…	…	…	…	…
am1	am2	…	amj	…	amn	bm

x1	x2	…	xj	…	xn
		…	0	…
		…	0	…
…	…	…	…	…	…	…
		…	1	…
…	…	…	…	…	…	…
		…	0	…

Алгоритм кроку перетворень Гауса-Жордана, тобто перехід від табл. 4.4 до табл. 4.5, такий:

1. усі елементи розв'язувального рядка табл. 4.4 ділимо на розв'язувальний елемент а_ij≠0 і результат записуємо в i–й рядок табл. 4.5;

2. усі елементи розв'язувального стовпця, крім a_ij замінюємо нулями;

3. решту елементів табл. 4.5 обчислюємо за формулами:

,

(k= 1, 2, …, i–1, i+1, …, m; l= 1, 2, …, j–1, j+1, …, n).

Е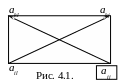 лементи і зручно обчислювати за правилом пря­мокутника. Розглянемо прямокутник, одна з вершин котрого лежить в елементі, на місці якого обчислюється новий, а протилежна – в розв'язувальному елементі; дві інші вершини лежать відповідно: одна в розв'язувальному рядку, а друга – розв'язувальному стовпці (рис.4.1.).

Елемент a_kl' (або b_k') дорівнює добутку розв'язувального елементу на протилежний йому елемент мінус добу­ток двох інших елементів і весь цей вираз ділиться на розв'язувальний елемент a_ij.

Зауваження.

1. Як розв'язувальний елемент зручно брати елемент, що дорівнює 1.

2. Якщо a_il = 0, то , тобто 1–й стовпець табл.4.4 записують без будь–яких змін у 1–й стовпець табл.4.5. 3. Якщо a_kj = 0, то , , тобто k–й рядок табл.4.4 без змін записують в k–й рядок табл.4.5.

Правильність обчислень можна проконтролювати в такий спосіб. Нехай a_ij – розв'язувальний елемент, а α_i – сума всіх елементів i–го рядка в табл.4.5:

(і = 1, 2, . . . , т) .

Покажемо, що в табл.4.5:

(k= 1, 2, …, i–1, i+1, …, m)

обчислюється за формулою

,

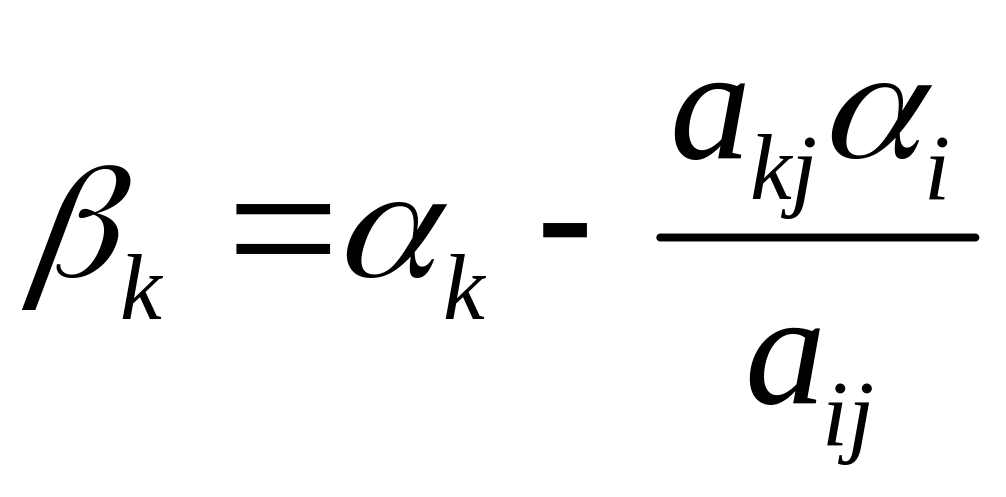тобто за тією самою формулою, за якою обчислюються всі елементи табл.4.5. Справді, оскільки в табл. 4.5

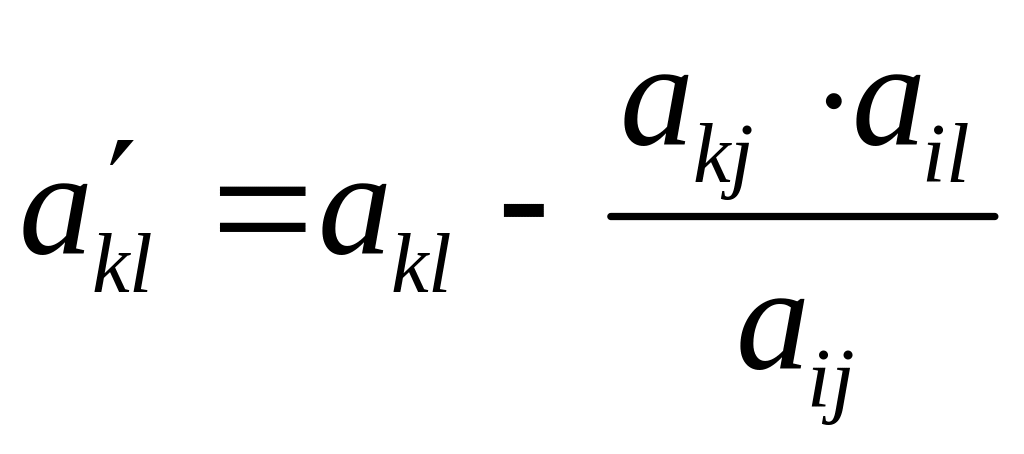(l= 1, 2, …, j–1, j+1, …, m); ,

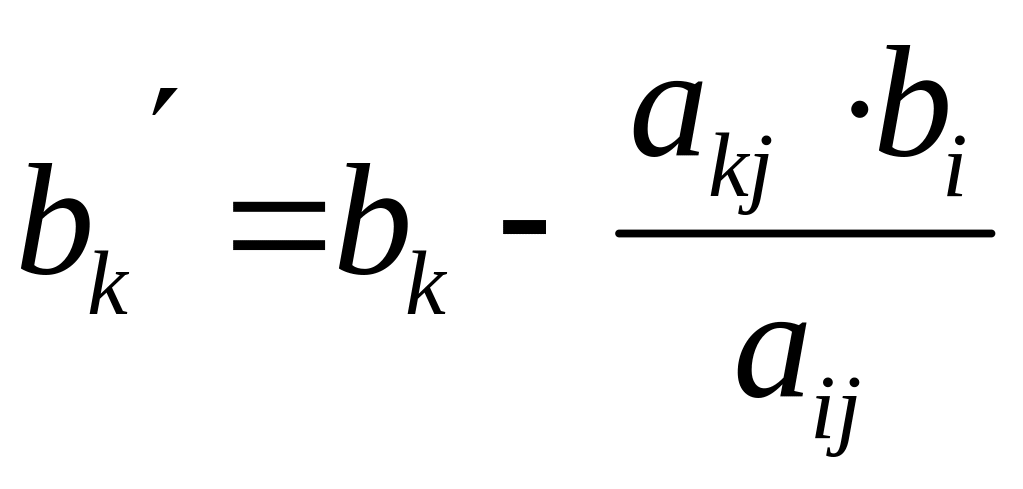то

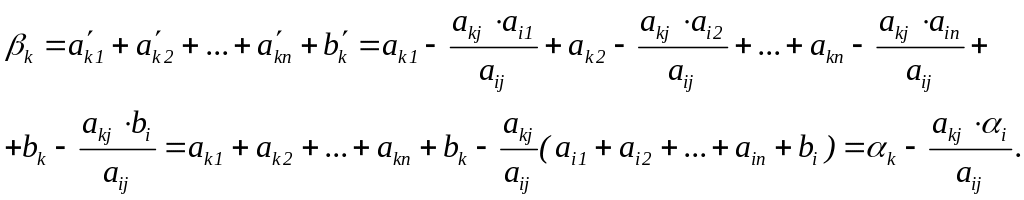
Отже, щоб проконтролювати правильність кроку перетво­рень Гаусса-Жордана в табл. 4.4 і 4.5 записують конт­рольний стовпець K. У табл. 4.5 елементи контрольного стовпця обчислюють як суму

,

а також за формулою

.

Якщо при цьому значення β_k збігаються, то елементи k–го рядка обчислено правильно.

Приклад. Розв'язати систему лінійних рівнянь методом Гаусса–Жордана [3].

Розв'язання. Результати обчислення подано в таблиці 4.6

Таблиця 4.6

x1	x2	x3	bi	K
2	–4	3	1	2
1	–2	4	2	6
3	–1	5	3	9
0	0	– 5	–5	–10
1	–2	4	3	6
0	5	–7	–7	–9
0	0	1	1	2
1	–2	0	–1	–2
0	5	0	0	5
0	0	1	1	2
1	0	0	–1	0
0	1	0	0	1

Отже, система сумісна і має розв’язок х₁=–1, х₂=0, х₃=1.

Обчислення оберненої матриці методом Гаусса–Жордана

Нехай задано неособливу квадратну матрицю по­рядку n

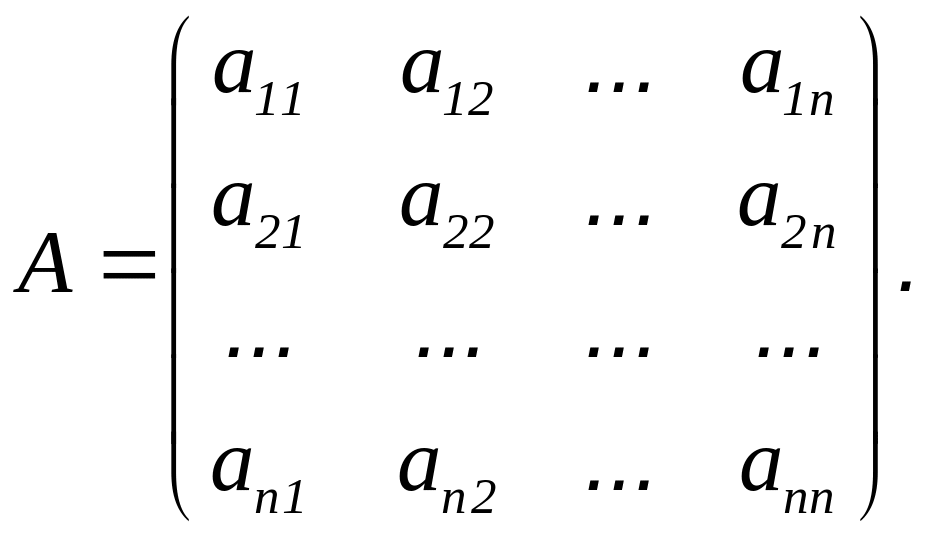
Розглянемо систему n лінійних рівнянь з n невідомими, записану у векторно–матричній формі AX=B, де X – вектор–стовпець невідомих; В – вектор–стовпець вільних членів. За допомогою цієї системи знайдемо обернену матрицю

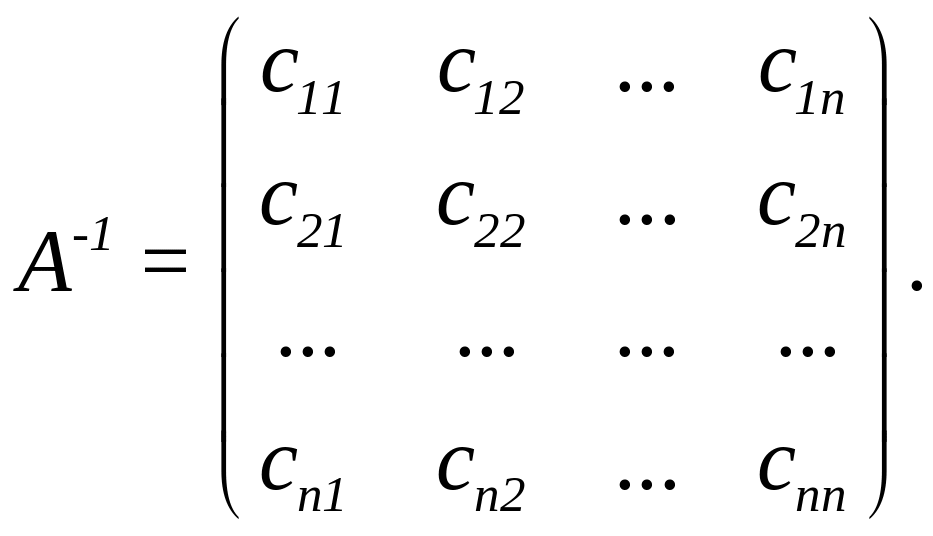
Покладемо послідовно , , …, .

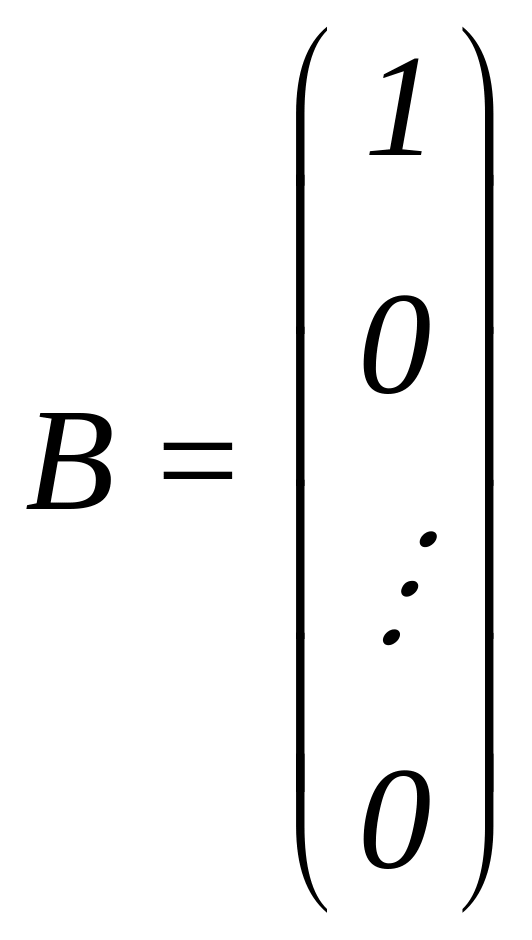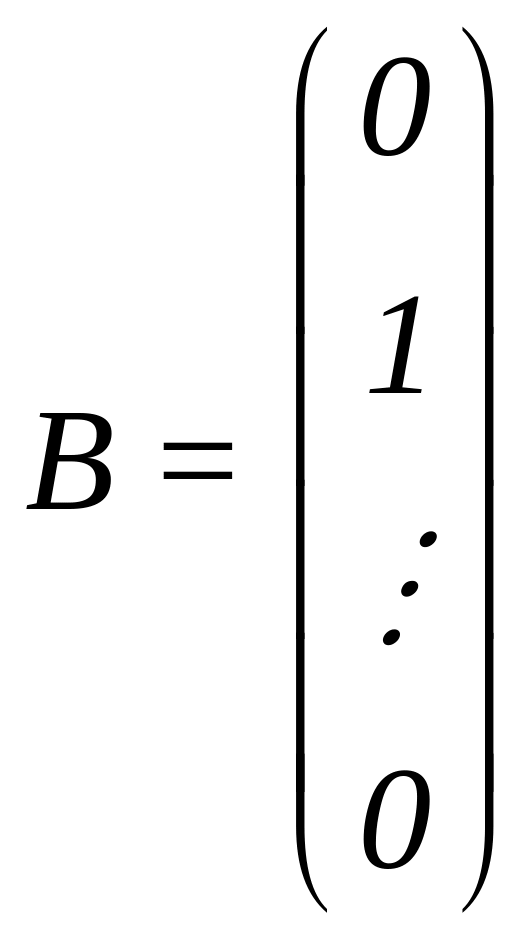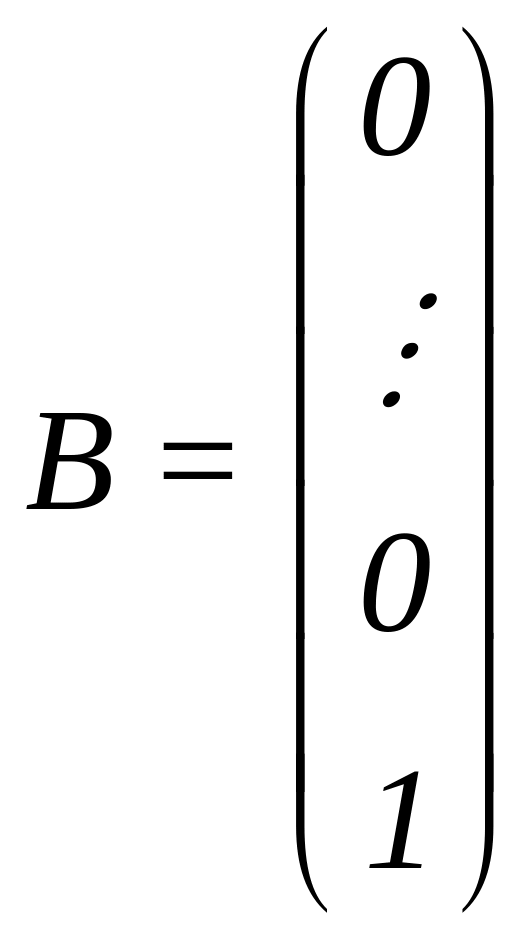Якщо , то .

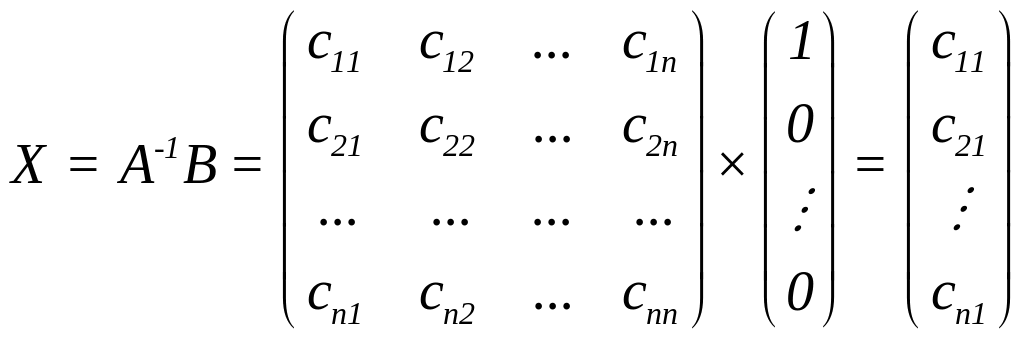Якщо , то .

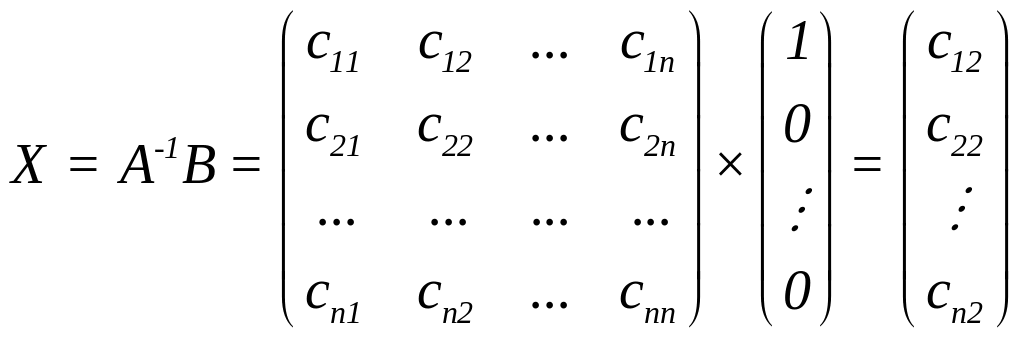Якщо , то .

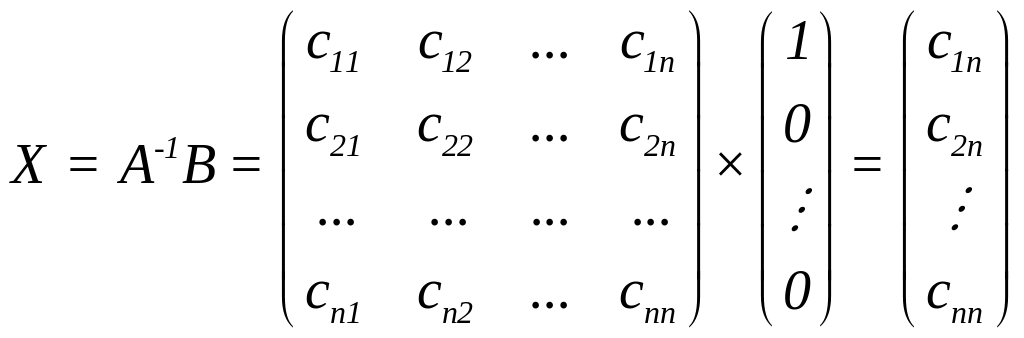Таким чином, розв'язки п систем АХ = В при

, , ...,

визначають відповідно 1–й, 2–й, ..., n–й стовпці обернено матриці А^–1.

Ці п систем, що відрізняються тільки вільними членами, можна розв'язувати одночасно і методом Гаусса–Жордана, записавши їх в одній таблиці. Стовпці вільних членів утво­рюють одиничну матрицю Е. Якщо розв'язувальні елементи вибирати по головній діагоналі, то після п кроків перетворень Гаусса–Жордана в таблиці на місці матриці А дістанемо одиничну матрицю Е, а на місці одиничної матриці – обернену матрицю А^–1. Якщо розв'язувальні елементи виби­рати довільно, то в останній таблиці треба рядки переставити так, щоб матриця стала одиничною.

Якщо обернену матрицю знаходять за методом Гаусса– Жордана, то не треба досліджувати задану матрицю на осо­бливість чи на неособливість, обчислюючи її визначник. Якщо можливе число кроків перетворень r менше від порядку матриці п (r < п), то матриця особлива і оберненої немає.

Приклад 1. Знайти обернену матрицю для матриці

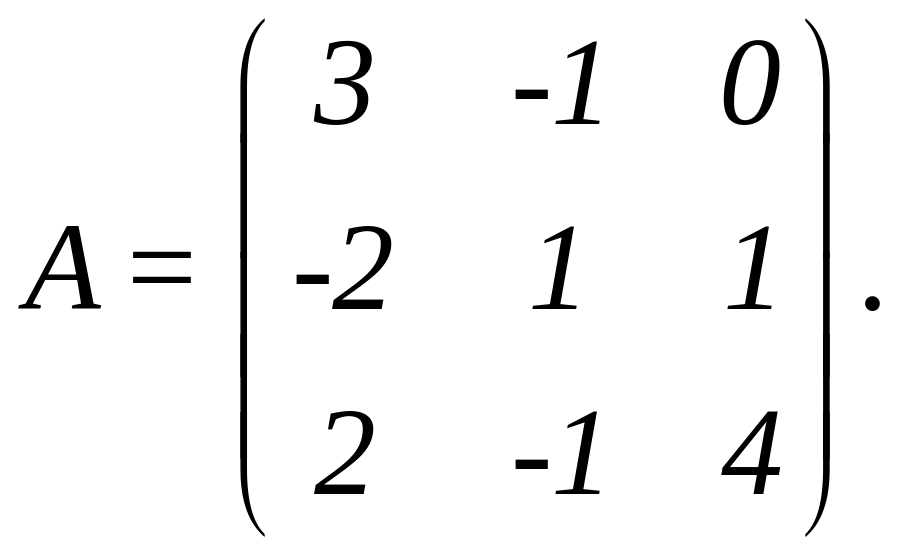
Розв’язання наведено у таблиці 4.7

Таблиця 4.7

A	E	K
1 0 1	1 1 0	4
0 1 3	2 3 0	9
0 0 5	0 1 1	7
1 0 0	1
0 1 0	2
0 0 1	0

A	E	K
3 –1 0	1 0 0	3
– 2 1 1	0 1 0	1
2 –1 4	0 0 1	6
1 0 1	1 1 0	4
–2 1 1	0 1 0	1
0 0 5	0 1 1	7

Отже, .

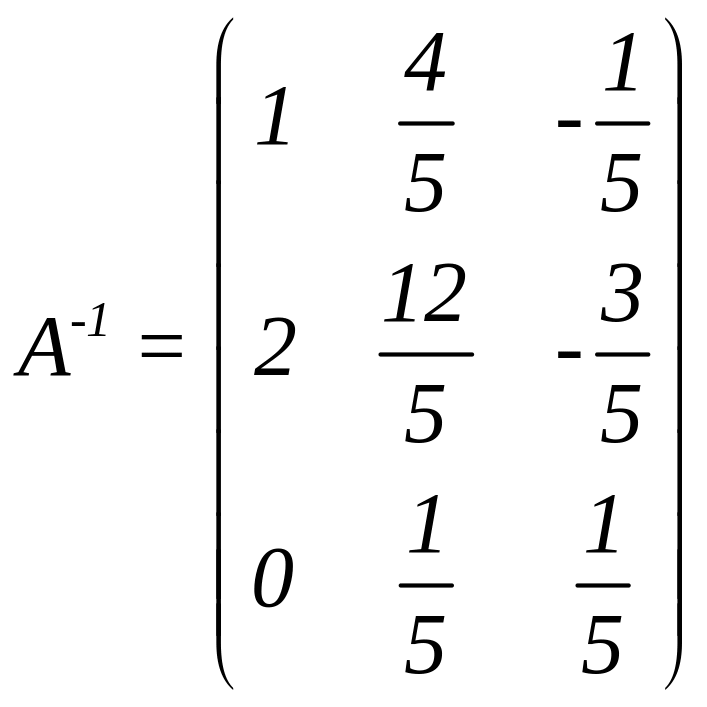Приклад 2. Знайти обернену матрицю для матриці

.

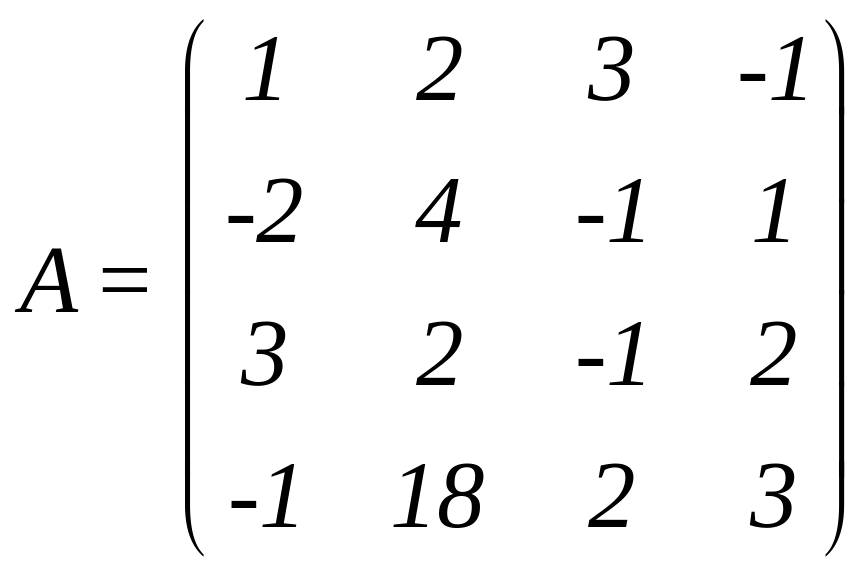Розв’язання. Складемо табл. 4.8 і виконаємо над її елементами максимально можливе число кроків перетворень Гаусса-Жордана.

У таблиці виконано r = 3 кроків виключень Гаусса-Жордана, а п =4(r<п), тому матриця А є особливою і оберненої матриці А^–1 немає.

Зазначимо, що за допомогою виключень методу Гаусса-Жордана можна також обчислити визначники n–го порядку.

Таблиця 4.8

А	Е	К

Згідно з властивістю 5 визначників кожний крок перетво­рень Гаусса-Жордана не змінює величини визначника, якщо множити його на розв'язувальний елемент. Виконуючи над елементами визначника п кроків перетворень Гаусса-Жор­дана, зводимо його до вигляду, коли всі елементи кожного рядка і стовпця, крім одного (який дорівнює одиниці), дорівнюють нулю. Переставивши в такому визначнику рядки або стовпці між собою, зведемо його до діагонального вигляду. Якщо при перетвореннях визначника дістаємо рядок або стовпець, складений з нулів, то такий визначник дорівнює нулю.