3.4. Обернення матриць за допомогою розбиття її на клітини

Для знаходження оберненої матриці можна використовувати метод розбиття на клітини. Нехай 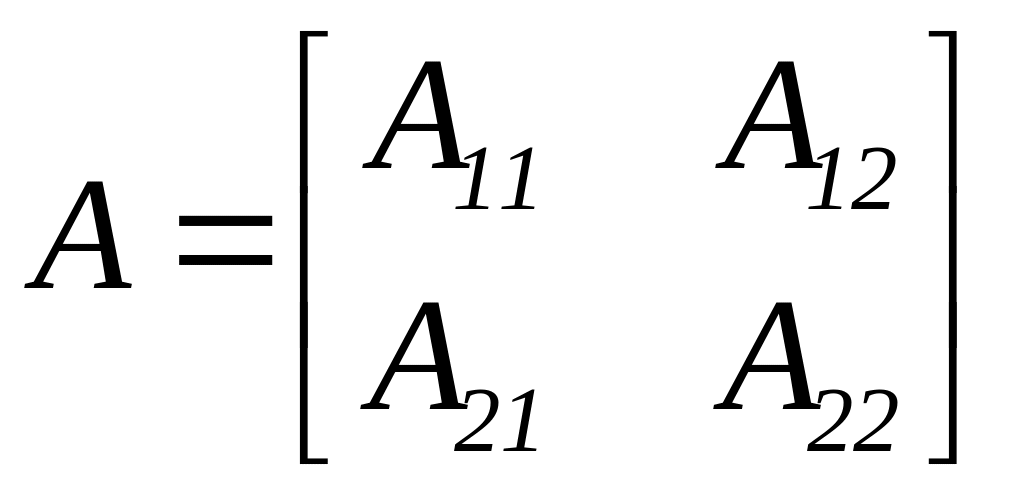клітинна неособлива матриця –го порядку, в якій і – квадратні клітини порядків p і q (де p+q= ). Необхідно знайти обернену матрицю 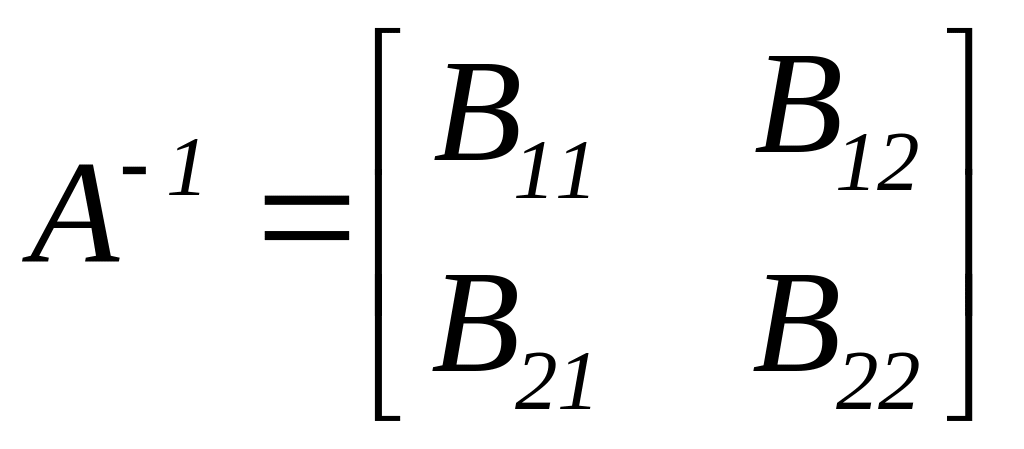у якій і – квадратні матриці також порядків p і q.

Відповідно визначенню оберненої матриці В даному випадку одинична матриця також буде розбита на клітини аналогічно, іншими словами 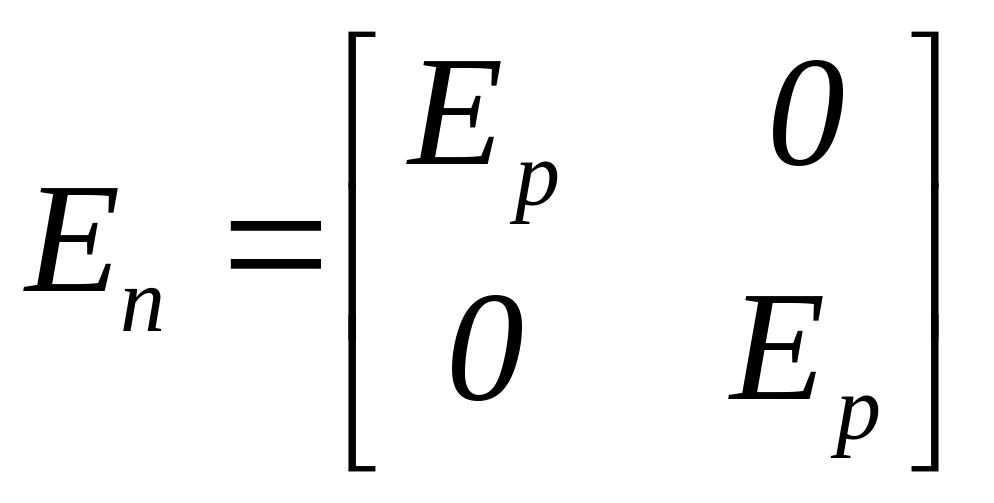, де і – одиничні матриці відповідно порядків p і q. Тоді 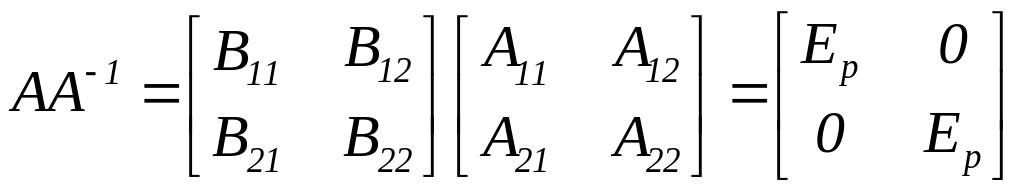, звідки після множення отримаємо чотири матричних рівняння:

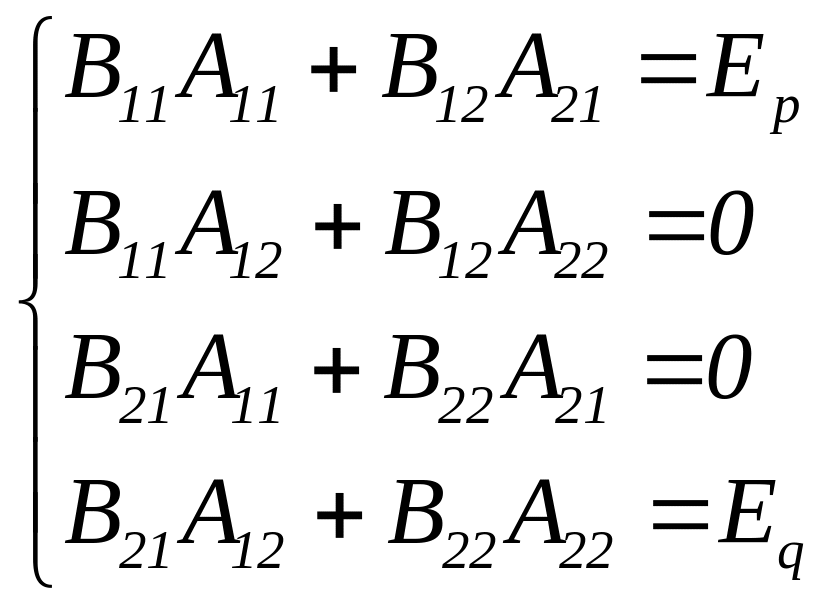. (3.13)

Для того, щоб знайти клітини матриці , потрібно розв’язати систему матричних рівнянь (3.13). Для цього використаємо спосіб виключення невідомих. Помножимо справа перше рівняння системи (3.13) на і віднімемо від результату множення друге рівняння цієї системи; отримаємо Звідси знаходимо

Аналогічно, з третього і четвертого рівняння системи (3.13) знаходимо Це можливо при умові, що відповідні операції мають смисл.

Введемо такі значення:

тоді формули для клітин матриці можна записати у вигляді:

(3.14)

Формули (3.14) справедливі при умові, що і існують. Обчислення зручно розмістити в вигляді такої схеми:

Обернена матриця має вигляд

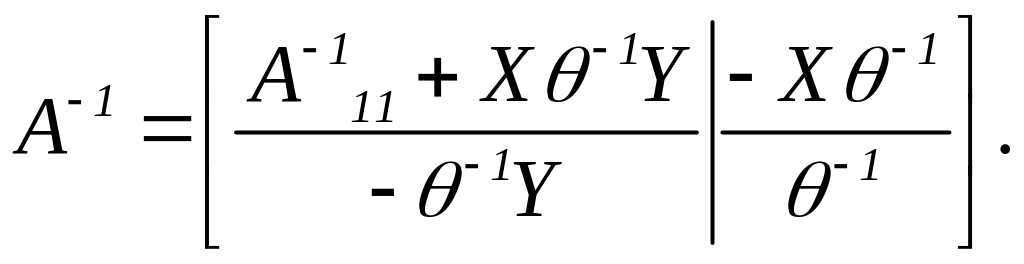
Приклад. За допомогою розбиття на клітини обернути матрицю

.

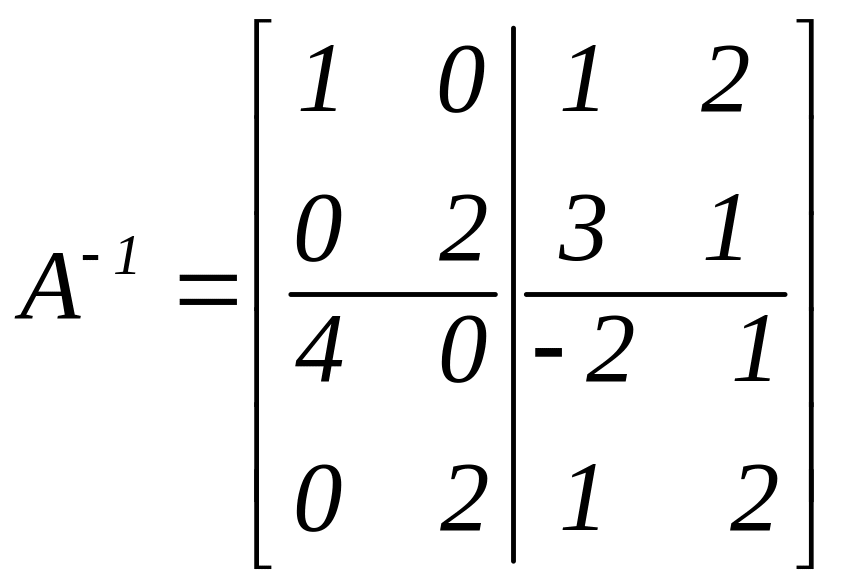Позначимо .

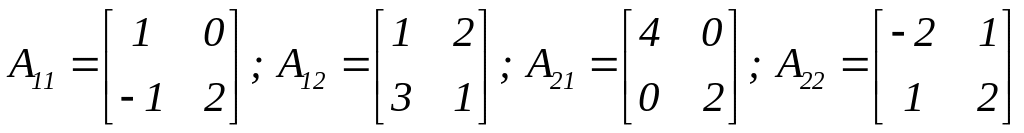Виконуємо необхідні обчислення:

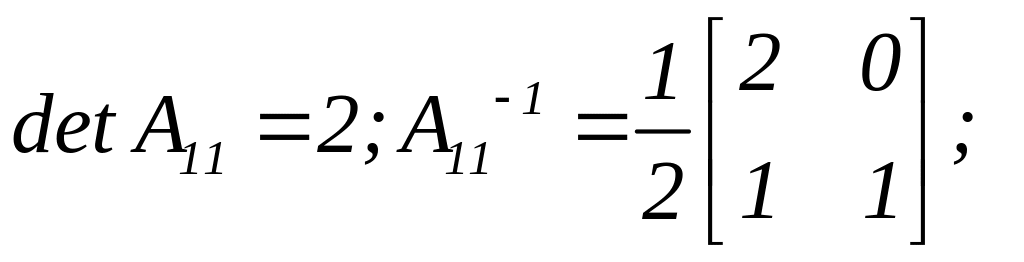
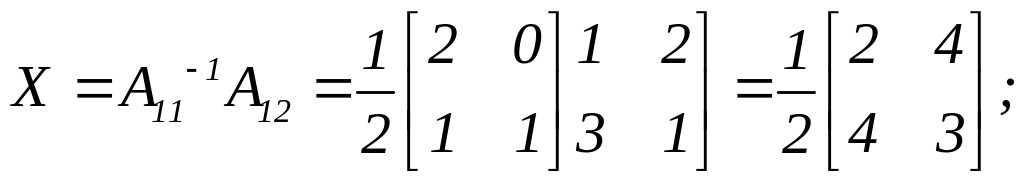
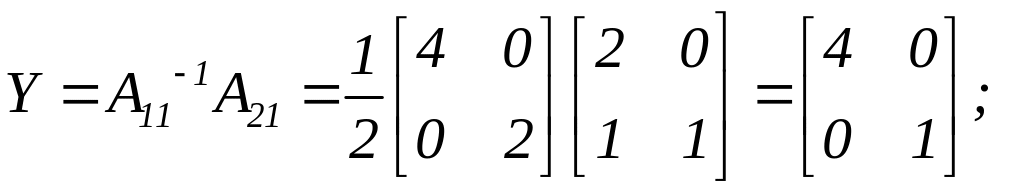
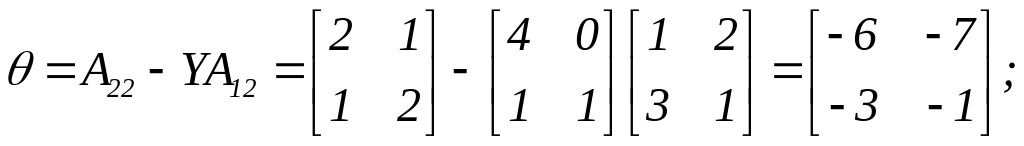
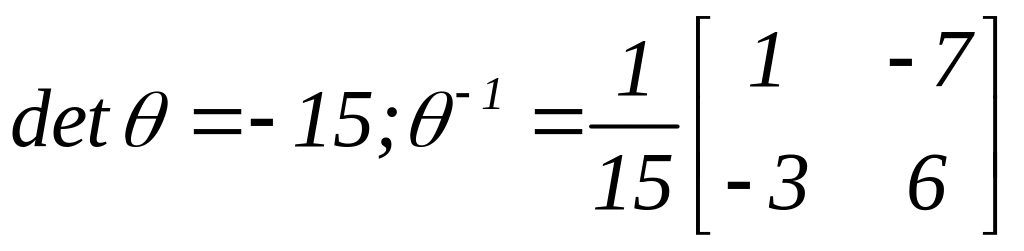
Запишемо початкові дані і результати обчислень в таблицю

Далі, маємо

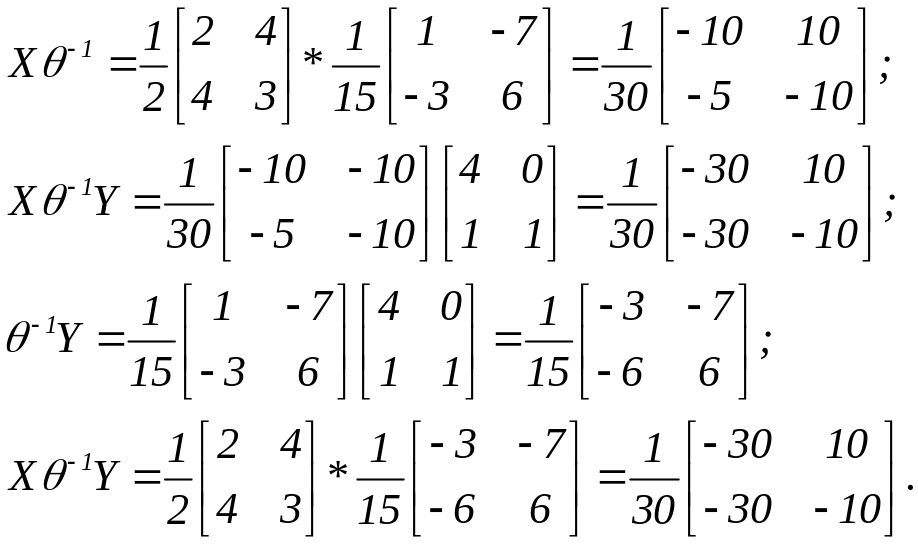
Для контролю добуток було обчислено двома способами.

= і = .

Кінцевий результат

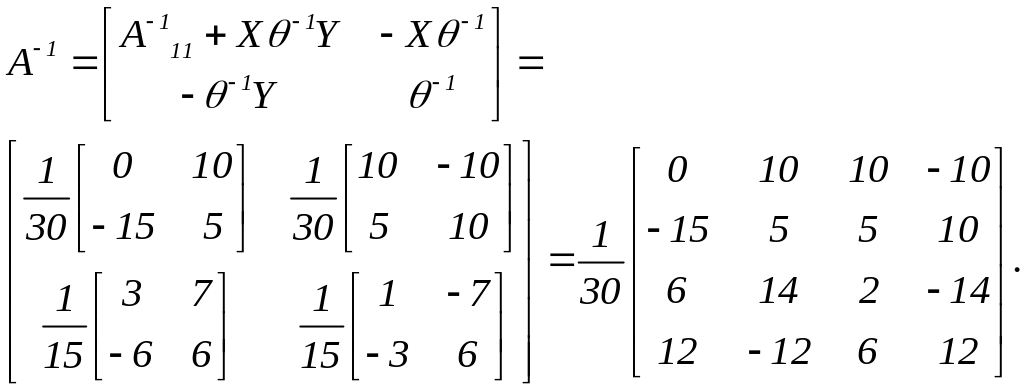
Особливим випадком даного метода обернення клітинних матриць є метод послідовного каймування.

Нехай дана квадратна неособлива матриця A n–го порядку, для якої необхідно знайти обернену матрицю .

Складемо послідовність матриць:

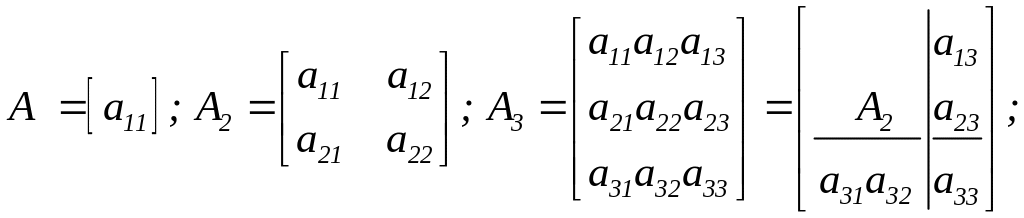
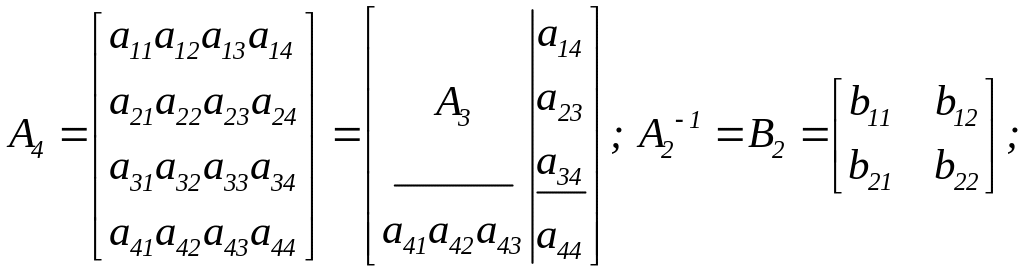
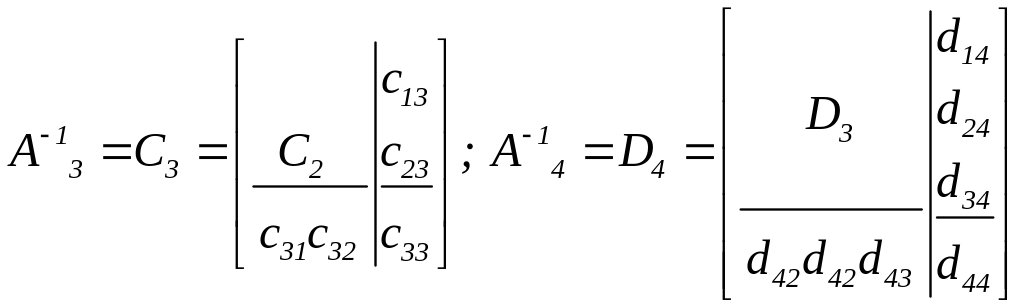і т.д.

Кожна наступна матриця отримана з попередньої окаймуванням.

Обернена до другої з цих матриць знаходиться безпосередньо: ,

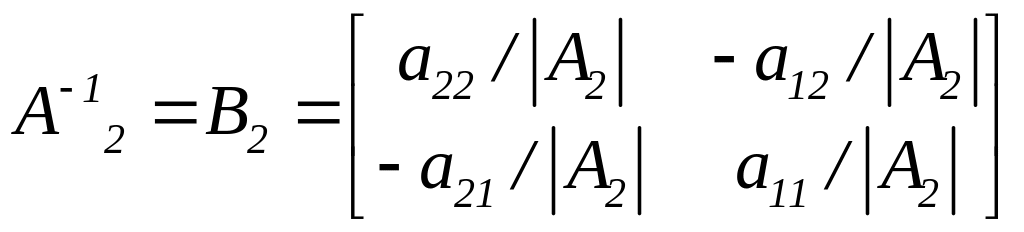де .

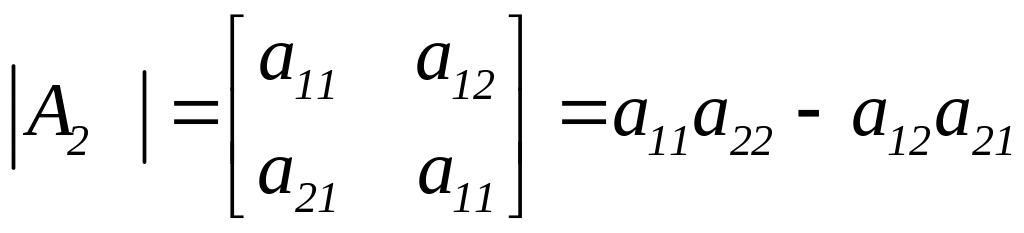За допомогою матриці , використавши до приведену вище схему обчислення, можна отримати , а потім за допомогою аналогічно отримати і т.д., насамкінець знайти .

Приклад 2. Методом послідовного окаймування обернути матрицю

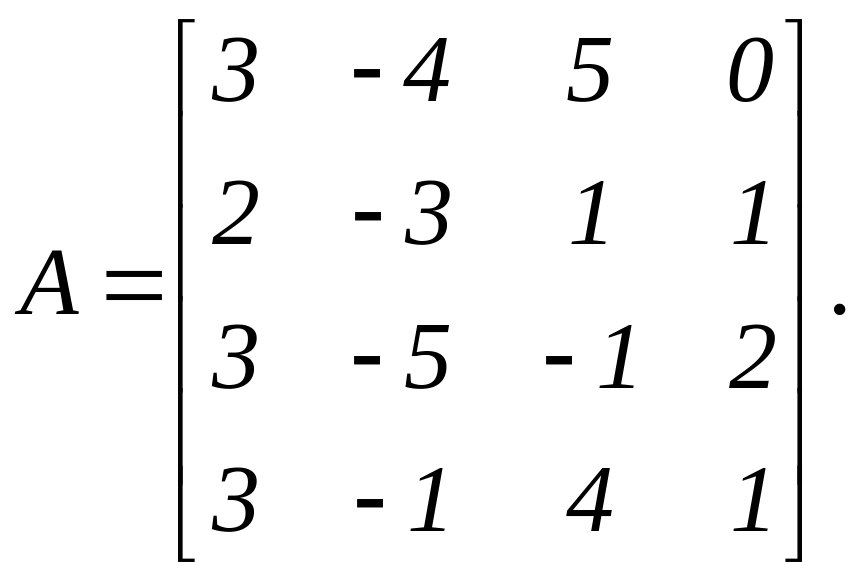
Маємо 1)

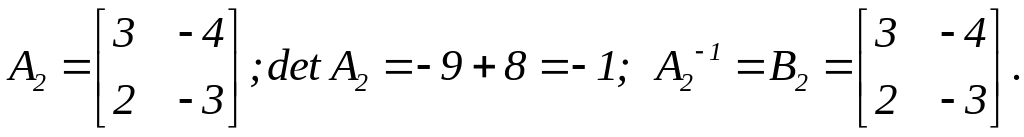
2) Схема обчислень має такий вигляд:

Виконуємо обчислення:

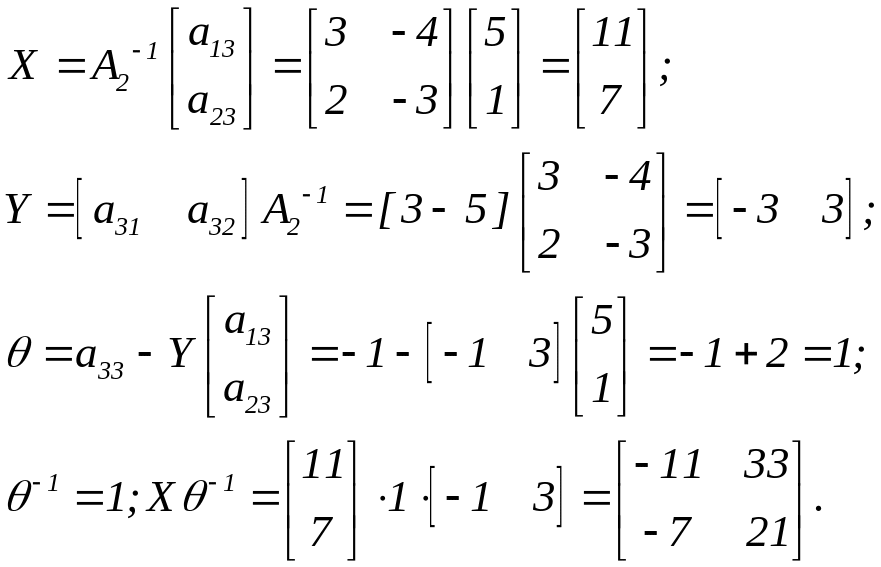
Заповнюємо схему

	3 –5	–1
11 7	2 –4 3 –3	5 1
1	–1 3	1

Елементи оберненої матриці отримуємо після нижченаведених дій:

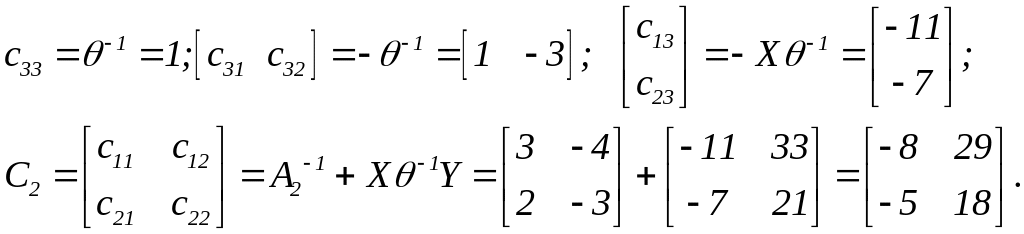
Таким чином .

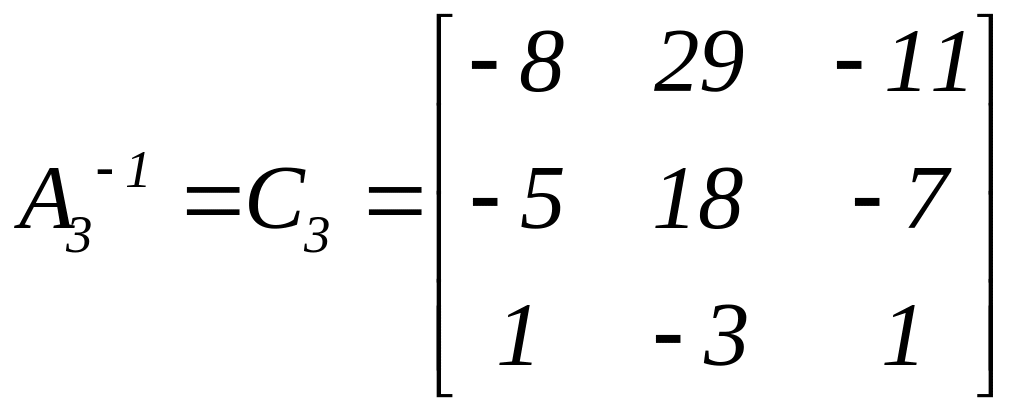3) Для обчислення складаємо схему:

Виконуємо обчислення:

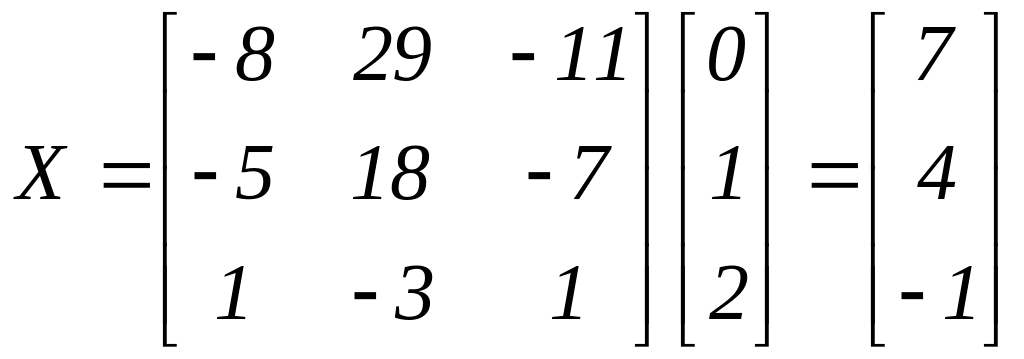
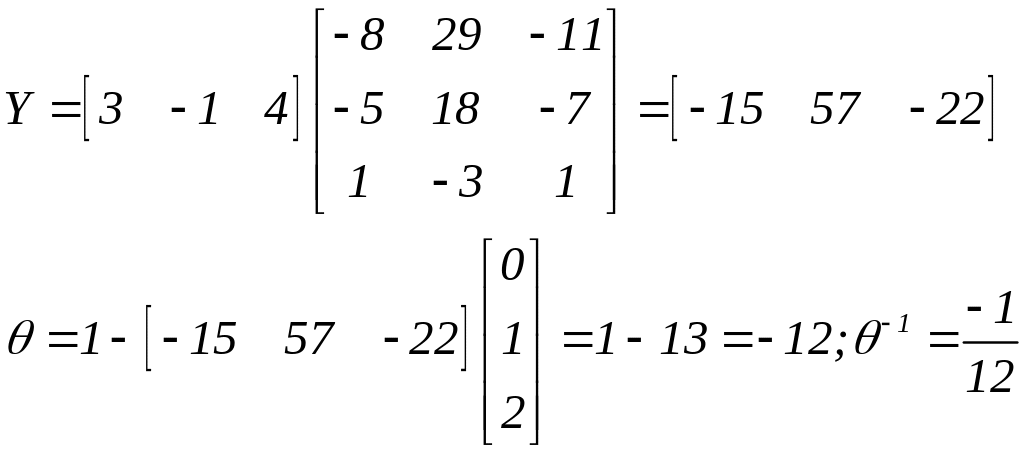
Заповнюємо схему:

	3 –1 4	1
7 4 –1	–8 29 11 –5 18 –7 1 –3 1	0 1 2
–1/12	–15 57 –22	–12

Далі маємо:

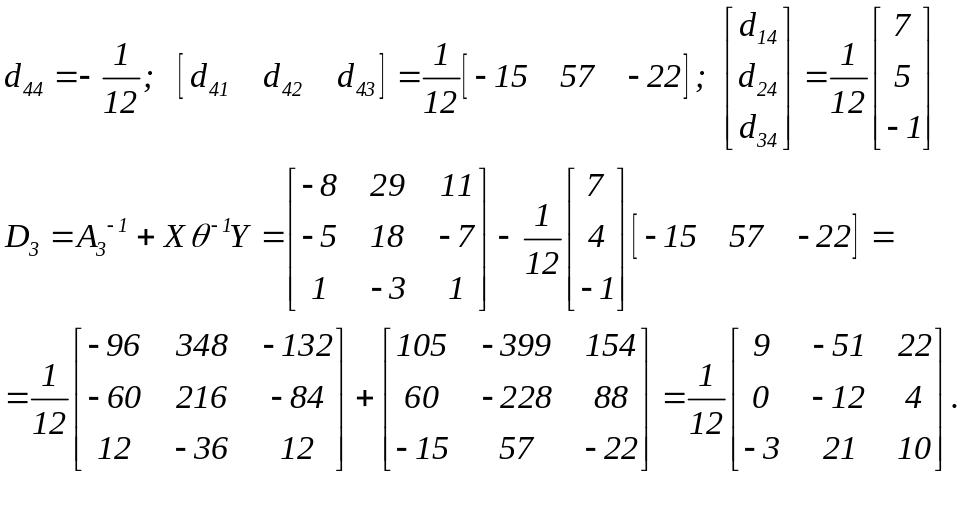
Отже,

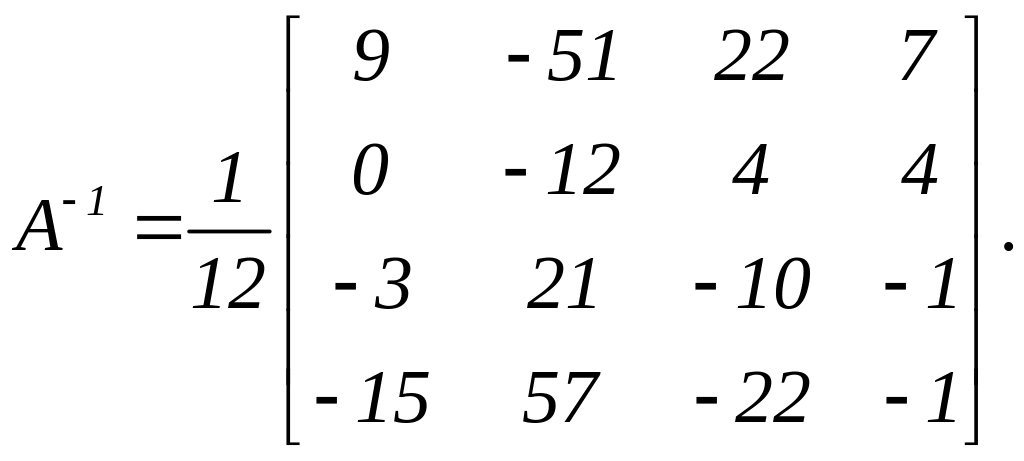
Метод окаймування можна використовувати тільки в тому випадку, якщо усі проміжні матриці неособливі.

Абсолютна величина і норма матриці

Абсолютною величиною (модулем) матриці є матриця , де всі елементи – модулі елементів матриці А [4].

Нехай А і В – матриці, для яких операції А+В і АВ мають смисл, тоді де – число.

Під нормою матриці розуміється дійсне число , що задовольняє такі умови [4]:

1) (при чому =0 тоді і тільки тоді, коли А=0);

2) , де – число (при чому = );

3) 4) 5) ,

де А і В – матриці, для яких відповідні операції мають cмисл.

Для матриці довільного розміру розглянемо три таких легкообчислювальних норми:

1) – максимальна сума модулів елементів матриці по рядках;

2) – максимальна сума модулів елементів матриці по стовпцях;

3) 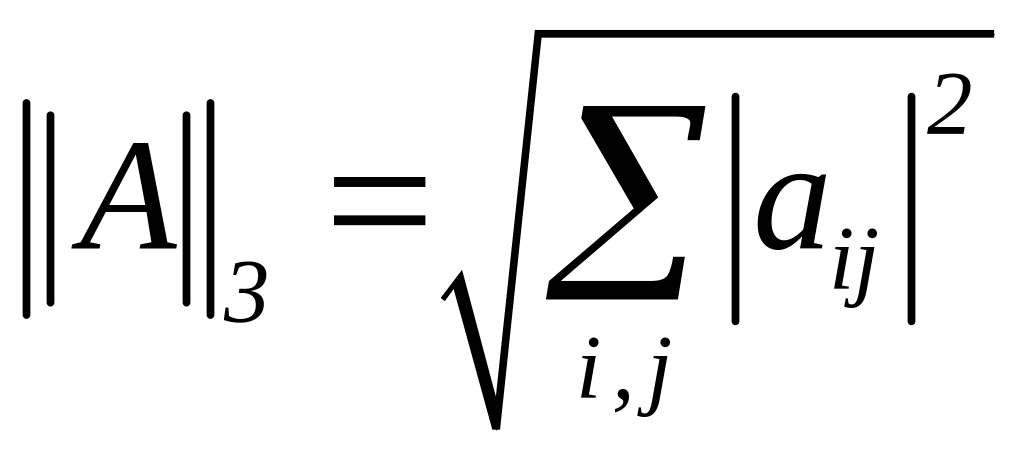– квадратний корінь із суми квадратів модулів всіх елементів матриці.