I стадия II cтадия III и IV cтадии

ATC_min АVC

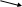AVC_min

MC_min

AFC

0 Q

Q_C Q_B Q_A

Рис. 8.2. Издержки производства в краткосрочном периоде

Суммирование FС и VС дает в итоге общие издержки (ТС – total cost). Для фирмы общие издержки – это наименьшие общие денежные затраты, необходимые для производства определенного объема продукции. По мере роста выпуска продукции ТС увели­чиваются, т.е. являются возрастающей функцией объема производства. На гра­фике кривая ТС полностью повторяет кривую VС, но сдвинута от нее вверх на величину постоянных издержек, так как ТС = FС + VС.

Для принятия обоснованных управленческих решений менеджерам важно знать не только общую сумму издержек, но и уровень средних издержек, т.е. из­держек, приходящихся на единицу продукции. Сопоставление средних издержек с ценой по конкретному продукту показывает, является ли производство продук­та прибыльным или убыточным.

Выделяют следующие виды средних издержек:

– средние общие издержки (АТС). Их формула: АТС = ТС/Q;

– средние постоянные издержки (АFС). Их формула: АFС = FС/Q;

– средние переменные издержки (АVС). Их формула: АVС = VС/Q.

Взаимосвязь между различными видами средних издержек выражается в следующей формуле:

АТС = АFС + АVС.

Наряду с перечисленными видами издержек, приходящихся на единицу продукции, в теории выделяют также предельные издержки. Для фирмы страте­гически важно определение предельных издержек, которые предприятие имеет возможность полностью контролировать. С помощью предельных издержек предприятие может точно определить, во что ему обойдется расширение произ­водства на одну дополнительную единицу продукции, и какие расходы предпри­ятие сэкономит при сокращении производства на одну единицу.

Предельные издержки (МС – marginal cost) - это дополнитель-ные издержки, связанные с производством дополнительной единицы продукции. Они определяются по следующей формуле:

МС = ТС/Q => МС = dТС/dQ,

т.е. предельные издержки равны производной функции общих издержек по объему производства. Поскольку ТС есть сумма FС и VС, и в этой сумме FС есть величина постоянная, производная которой равна нулю, то МС = dVС/dQ, т.е. предельные издержки равны также производной функции переменных из­держек по объему производства.

Для решения вопросов определения оптимального объема выпуска про­дукции менеджерам фирмы надо знать, как изменяются средние и предельные издержки с ростом объема производства.

Средние общие издержки, так же, как и предельные издержки для любых объемов выпуска, могут быть определены из кривой общих затрат.

Исходя из того, что АТС = ТС/Q, средние общие издержки для какого-то объема выпуска равны тангенсу угла наклона луча, проведенного из начала ко­ординат и через точку на кривой ТС, соответствующую этому объему выпуска. Например, средние общие издержки в точке А, которой соответствует объем вы­пуска Q_A, составляют ТС_A/Q_A, т.е. равны тангенсу угла наклона луча 0А. Этот луч в точке A касается кривой ТС.

При объеме производства Q_A средние общие издержки являются мини­мальными, потому что тангенсы углов наклона лучей, проведенных через другие точки кривой ТС, будут больше тангенса угла наклона луча ОА. Причем, при росте производства от 0 до Q_A средние общие издержки будут уменьшаться, а при увеличении производства после Q_A – возрастать. Таким образом, кривая АТС имеет форму параболы. Это соответствует характеру изменения средней произ­водительности переменного фактора. Пока при увеличении объема выпуска средняя производительность растет, АТС уменьшаются, но с момента уменьше­ния среднего продукта АТС начинают возрастать. Точка минимума АТС совпа­дает с точкой максимума среднего продукта.

Подобным же образом можно описать и кривую АVС. В этом случае тан­генс угла наклона луча, выходящего из начала координат и касательного к кри­вой VС в точке В, соответствует минимальному значению АVС. Средние пере­менные издержки также описываются параболической кривой.

Следует заметить, что Q_A > Q_B, а это значит, что АТС становятся минимальными при большем объеме выпуска, чем АVС.

Функция средних постоянных издержек является убывающей функцией, имеющей форму гиперболы. При выпуске небольшого количества продукции на одну единицу товара приходится значительная величина постоянных издержек. При увеличении объема производства средние постоянные издержки снижаются, и кривая АFС асимптотически приближается к оси абсцисс.

Поскольку АFС с ростом объема производства стремятся к нулю, то кри­вые АVС и АТС по мере увеличения Q сближаются. Следует принять во внима­ние, что расстояние между кривыми АТС и АVС равно величине АFС, так как АТС - АVС = АFС.

Так как предельные издержки МС = dTС/dQ, то их величина для опреде­ленного объема продукции равна тангенсу угла наклона касательной, проведен­ной через точку на кривой ТС, соответствующую этому объему производства.

Если вдоль кривой ТС провести касательные к ее точкам и проследить, как изменяется величина тангенса угла их наклона (т.е. величина МС), то карти­на получается следующая: вначале МС, т.е. тангенсы углов наклона касатель­ных, уменьшаются и достигают минимального значения в точке С, которая явля­ется точкой перегиба кривой ТС, а затем по мере роста производства МС возрас­тают. Таким образом, кривая МС тоже имеет параболическую форму. Это соот­ветствует действию закона убывающей отдачи: на начальном этапе роста выпус­ка, когда предельный продукт растет, МС уменьшаются, а с момента убывания предельного продукта МС возрастают. Точка минимума МС совпадает с точкой максимума предельного продукта.

Как предельные издержки соотносятся с АТС и АVС? МС = АТС тогда, когда АТС минимальны. Доказательство этого положения следующее:

выше было выяснено, что АТС минимальны, когда объем выпуска равен Q_A. При этом АТС равны тангенсу угла наклона луча 0А. Но луч 0А является касательной к кривой ТС в точке А. Поэтому тангенс угла наклона луча 0А одновременно равен вели­чине МС. Таким образом, МС = АТС, когда АТС минимальны.

Точно так же можно доказать, что МС = АVС, когда АVС минимальны.

При анализе производственной функции в краткосрочном периоде произ­водство было разделено на четыре стадии. Рассмотрим эти производственные стадии с позиций поведения издержек производства в краткосрочном периоде.

Стадия I начинается от нулевого уровня выпуска до точки максимально­го предельного продукта переменного фактора. Средний продукт на этой стадии растет. С точки зрения издержек на этом временном интервале происходят сле­дующие изменения: предельные издержки уменьшаются и достигают минимума при максимальном предельном продукте, средние общие издержки тоже снижа­ются.

Стадия II соответствует такому уровню выпуска, при котором предель­ный продукт уменьшается, но он еще пока больше среднего продукта, поэтому средний продукт растет и достигает максимального значения, когда сравнивает­ся с предельным продуктом. На этом производственном интервале предельные издержки возрастают а средние общие издержки уменьшаются до тех пор пока не сравниваются с предельными издержками. В точке равенства МС и АТС средние общие издержки достигают минимума.

На Ш стадии средний продукт переменного фактора уменьшается, предельный продукт, будучи положительным, тоже уменьшается и достигает нулевого уровня. На этом интервале вместе с выпуском увеличиваются и сред­ние, и предельные издержки.

На IV стадии процесс производства идет при отрицательных значениях предельного продукта переменного фактора, и поэтому средние и предельные издержки возрастают очень быстро. Комбинации ресурсов на этой стадии не включаются в производственную функцию.