4. Биноминальное распределение, его числовые характеристики.

Биномиальным называется закон распределения дискретной случайной величины Х- числа появлений события А в n независимых повторных испытаниях, в каждом из которых события А может наступить с вероятностью p или не наступить с вероятностью q=1-p. Тогда Р(Х=m)-вероятность появления события А ровно m раз в n испытаниях вычисляется по формуле Бернулли:

Р(Х=m)=С^m_np^mq^n-m

Математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины Х, распределенной по бинарному закону, находят, соответственно, по формулам:

M(X)=np,

D(X)=npq,

Если число испытаний n очень велико, а вероятность появления события А в каждом испытании очень мала (р≤0,1), то для вычисления Р(Х=m) используют формулу Пуассона:

Р(Х=m)=Р_n(m)= e^-λ • λ^m , где λ=np

^{m !}

Тогда говорят, что случайная величина Х - распределена по закону Пуассона.

Так как вероятность р события А в каждом испытании мала, то закон распределения Пуассона называется законом средних явлений.

5. Равномерное распределение, его числовые характеристики.

Непрерывная случайная величина Х имеет равномерный закон распределения на некотором интервале (а;b), которому принадлежат все возможные значения Х, если плотность распределения вероятностей f(x) постоянная на этом интервале и равна 0 вне его, т.е.

0 при х≤а,

f(х)= при a<х<b,

0 при х≥b .

График функции f(x) изображен на рис. 1

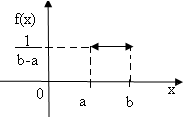
(рис.1) (рис.2)

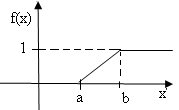
Функция распределения случайной величины Х, распределенной по равномерному закону, задается формулой:

0 при х≤а,

F(х)= при a<х≤b,

0 при х>b.

Ее график изображен на рис. 2.

Числовые характеристики случайной величины равномерно распределенной на интервале (a;b), вычисляются по формулам:

M(Х)= _, D(X)= , σ(Х)= _.

6. Нормальное распределение, его параметры. Вычисление вероятности попадания в интервал.

Непрерывная случайная величина Х имеет нормальный закон распределения (закон Гаусса), если ее плотность распределения имеет вид:

,

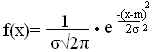где m=M(X), σ²=D(X), σ>0.

Кривую нормального закона распределения называют нормальной или гауссовой кривой (рис.7)

Н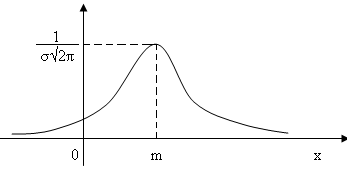 ормальная кривая симметрична относительно прямой х=m, имеет максимум в т. х=а, равный _.

рис.7

Функция распределения случайной величины Х, распределенной по нормальному закону, выражается через функцию Лапласа Ф (х) по формуле:

,

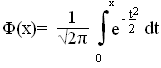где - функция Лапласа.

Замечание: Функция Ф(х) является нечетной (Ф(-х)=-Ф(х)), кроме того, при х>5 можно считать Ф(х) ≈1/2.

График функции распределения F(x) изображен на 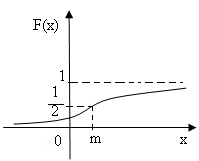рис. 8

рис.8

Вероятность того, что случайная величина Х примет значения, принадлежащие интервалу (a;b) вычисляются по формуле:

Вероятность того, что абсолютная величина отклонения меньше положительного числа δ вычисляется по формуле:

В частности, при m=0 справедливо равенство: