§10. Операторы векторного анализа (теории поля).

1. Градиент скалярного поля.

Градиент скалярного поля u = u(x,y,z) есть векторное поле grad u = .

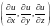2. Дивергенция векторного поля.

Определение. Дивергенцией векторного поля а называется скалярное поле

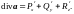
Теорему Гаусса – Остроградского можно теперь сформулировать следующим образом:

Поток векторного поля через замкнутую поверхность равен тройному интегралу по области

ограниченной этой поверхностью от дивергенции векторного поля.

Из теоремы Гаусса – Остроградского следует физический смысл дивергенции.

Пусть U_ε(M) – ε- окрестность т.М. По ф. Г – О. :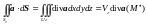 (по т. о среднем) . Отсюда : плотность потока векторного поля. Знак дивергенции в некоторой области определяется наличием в ней источников (diva> 0 ) или

стоков ( diva < 0 ).

Пример. Определить расположение источников и стоков поля .

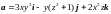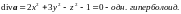{ Источники вне гиперболоида, стоки − внутри}

3. Ротор ( вихрь) векторного поля.

Определение. Ротором векторного поля а называется векторное поле равное:

Перечисленные операторы легко выражаются через символический вектор 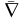( читается «набла»):

и называется оператором Гамильтона:

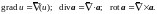
§11. Теорема (формула) Стокса.

Пусть в пространстве задано непрерывно дифференцируемое векторное поле а и кусочно-гладкая

ориентированная поверхность S с границей Г, ориентированной по S. В этом случае верна формула:

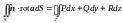(формула Стокса).

{ Доказательство этого утверждения аналогично доказательствам теорем Грина и Гаусса – Остроградского и здесь не приводится }

Таким образом, теорема Стокса утверждает, что поток ротора векторного поля через

. ориентированную поверхность равен циркуляции этого поля по границе поверхности

Замечания. 1. Формула Грина является частным случаем формулы Стокса для плоской области.

2.Из ф. Стокса следует, что поток ротора через поверхность зависит только от ее границы и

не зависит от ее формы поверхности.

Пример. Вычислить интеграл 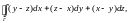где Г – линия пересечения цилиндра

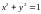с плоскостью 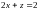(эллипс), пробегаемая против часовой стрелки, если смотреть с положительной стороны оси ОХ.

{

}

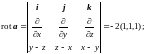
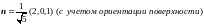
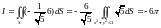§12. Потенциальные и соленоидальные векторные поля.

Определение потенциального поля было дано в §5 вместе с необходимыми и достаточными условиями потенциальности в плоском случае. Используя теорему Стокса, можно доказать более общее фундаментальное утверждение:

Теорема 1. Векторное поле потенциально в некоторой области тогда и только тогда, когда его ротор равен нулю в этой области.

{1. Поле а потенциально и u - его потенциал. Рассмотрим :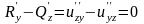 . Две другие координаты ротора так же равны нулю.

2. rota = 0. Из теоремы Стокса следует, что циркуляция по любому замкнутому контуру равна нулю, т.е. поле – потенциально ( §5).}

Определение. Векторное поле а называется соленоидальным в области G , если в этой области

поток поля через любую замкнутую поверхность области равен нулю.

Теорема 2. Векторное поле соленоидально тогда и только тогда, когда его дивергенция равна нулю.

{1. Поле соленоидально т.е. поток равен нулю 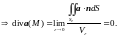(см.§10)

2. diva = 0 . Из теоремы Г−О сразу следует равенство нулю потока через замкнутую поверхность,

т.е. соленоидальность поля.}

Таким образом, соленоидальность поля внутри области характеризуется отсутствием как источников, так и стоков в этой области.