§7. Поверхностные интегралы 1-го рода.

Пусть дано скалярное поле u = f (x,y,z), (x,y,z) S = {z=z(x,y); (x,y) D}

Определение. Поверхностным интегралом 1-го рода от функции f (x,y,z) по поверхности S

называется интеграл

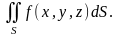
В простейшем случае он равен: = . В более общем –

= .

Теорема существования и все свойства криволинейных интегралов 1-го рода целиком переносятся

на поверхностные интегралы 1-го рода (гл.II, §2). Последняя теорема имеет формулировку:

Теорема. Поверхностные интегралы 1-го рода не зависят от ориентации поверхности:

Основные приложения – масса поверхности с поверхностной плотностью f (x,y,z) и все величины

с ней связанные: центр масс, моменты и т.д. При f ≡ 1 получим площадь поверхности.

Пример. Вычислить массу части поверхности z = x² + y² с плотностью μ = │xyz│, отсекаемой плоскостью z = 1.

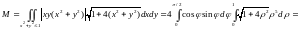
§8. Поверхностные интегралы 2-го рода.

Пусть на поверхности заданы векторное поле а и единичная нормаль n = (cosα, cosβ, cosγ).

Определение. Поверхностным интегралом 2-го рода по ориентированной поверхности S⁺ называется

интеграл

Подставляя координаты векторов a и n , получим

Величина cosαּdS равна элементу площади проекции поверхности на плоскость YOZ, т.е. dydz.

Аналогичные равенства имеют место для двух других слагаемых. Тем самым, представления

поверхностных интегралов 2-го рода имеют вид:

=

=

где S_YOZ , S_XOZ , S_XOY - проекции ориентированной поверхности S на координатные плоскости.

Пример. Вычислить интеграл нормаль − внешняя.

Рассмотрим 1-й интеграл:

Во втором интеграле : 1-ый минус, т.к. х ≤ 0, а второй – т.к. n образует острый угол с ( − i).

В результате имеем

Остальные интегралы равны первому. Ответ: 4πа³.

Так как поверхностный интеграл 2-го рода сводится к поверхностному интегралу 1-го рода ,то общие свойства и теорема существования сохраняются. Как и в случае криволинейных интегралов

2-го рода имеет место

Теорема. При изменении ориентации поверхности S, знак интеграла меняется на противоположный:

.

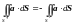Определение. Поверхностные интегралы 2-го рода называют потоком векторного поля через ориентированную поверхность.

§9. Теорема (формула) Гаусса – Остроградского.

Рассмотрим векторное поле а, определенное в области G трехмерного пространства. .

Теорема (формула) Гаусса – Остроградского. Пусть поле а непрерывно вместе с частными производными в области G, ограниченной кусочно-гладкой замкнутой поверхностью S, ориентированной по внешней нормали. В этом случае имеет место формула (ф. Г. – О.):

{ Пусть G_z правильная по z область, S_XOY ее проекция на XOY; z₁(x,y), z₂(x,y) и S_B нижняя, верхняя

и боковая границы области G_z . Рассмотрим

(Знак перед интегралом по z₁ изменился из-за нормали, а интеграл по S_B равен нулю)

Для областей, правильных по x и по y получим аналогичные формулы для P и Q.

Если область G может быть разбита на конечное множество областей, правильных по x , y и z,

то получаем формулу Гаусса – Остроградского.}

Пример (предыдущий).

{ (Утроенный объем шара)}