§5. Условия независимости криволинейных интегралов 2-го рода от пути интегрирования.

Особый интерес представляет собой случай, когда криволинейный интеграл 2-го рода не зависит от

пути интегрирования (достаточно вспомнить его физический смысл).

Теорема 1. Криволинейный интеграл 2-го рода не зависит от пути интегрирования тогда и только

тогда, когда соответствующий интеграл по замкнутому контуру равен нулю.

{ Необходимость: (Г₁ и Г₂ – 2 различные дуги, соединяющие точки А и В. Рассмотрим

замкнутую кривую АВА : .

Достаточность: . Обозначим Г₁ и Г₂ 2 кривые, соединяющие 2 произвольные точки контура Г.

. Теорема доказана. }

Определение потенциального векторного поля а = (P,Q,R), как градиента некоторого скалярного поля (его потенциала) u(x,y,z), было дано в §1 настоящей главы. Сделаем теперь два замечания относительно этих понятий:

1. Так как координаты потенциального векторного поля а: P, Q и R равны частным производным функции u по x,y и z соответственно, то дифференциальная форма Pdx+Qdy+Rdz является полным дифференциалом этой функции: du = Pdx+Qdy+Rdz.

2. Потенциал векторного поля определен с точностью до произвольной постоянной.

Из курса ФНП известно, что в плоском случае дифференциальная форма равна полному дифференциалу тогда и только тогда, когда .

( В пространстве имеют место соотношения: 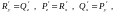что будет доказано ниже.)

Отсюда и из формулы Грина сразу следует

Теорема 2. Интеграл по замкнутому контуру от потенциального поля равен нулю.

Оказывается верным и обратное утверждение:

Теорема 3. Пусть интеграл по любому замкнутому контуру (в области интегрируемости) равен нулю.

В этом случае соответствующее векторное поле потенциально.

{ Так как 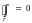, то по Т.1 он не зависит от пути интегрирования. Возьмем контур А₀А₁А₂ (рис.2) (отрезок А₁А₂ ║ОХ). Пусть т. .

Отсюда : (y и z − произвольные фиксированные

значения). Аналогично получим: .

Следовательно, существует функция, градиент которой

равен а , т.е. поле потенциально. }

Перечислим все необходимые и достаточные условия потенциальности для плоского случая:

Для потенциального поля верна формула Ньютона – Лейбница:

пусть u(x,y,z) – потенциал поля а = (P,Q,R)

Эту формулу можно использовать и в обратную сторону, т.е. определять функцию u(x,y,z) по

полному дифференциалу.

§6. Элементы теории поверхностей.

Поверхностью будем называть непрерывное отображение плоской области D на множество S

трехмерного пространства. В простейшем случае S: z = f (x,y), (x,y) D. Более общее задание − параметрическое: S={r(u,v); (u,v) W, или S={x(u,v),y(u,v),z(u,v); (u,v) W}.

Если r(u,v) – дифференцируемая функция, то поверхность называется гладкой. Векторы r_u, r_v и

dr = r_u du + r_v dv , лежат в касательной плоскости к S, а элемент площади равен: где .{б/д}

В частном случае явного задания S: z = z(x,y) или r(x,y,z) = r(x,y,z(x,y)), (x,y) D имеем: , или где (см. гл.1,§12).

Определение. Гладкая поверхность называется ориентируемой или двусторонней, если на ней можно выбрать единичную непрерывную нормаль (которая ее и ориентирует), и неориентируемой или односторонней в противном случае. (Примеры, лист Мебиуса)

В дальнейшем будем рассматривать только гладкие, ориентируемые поверхности.

Нормаль к ориентируемой поверхности равна вектору n = r_u×r_v и может иметь в каждой точке два значения: n и –n.

Если направление нормали задано, то ориентированную по ней поверхность обозначим S⁺, а противоположно ориентируемую – .