§3. Криволинейные интегралы 2-го рода.

Введем еще одно обозначение: пусть l – единичный вектор касательной к кривой Г в т.(x,y,z).

Как известно, l = dr/ds . Следовательно, l·ds = dr = (dx,dy,dz).Так как l – орт, то l=(cosα, cosβ, cosγ).

Рассмотрим теперь векторное поле a = (P(x,y,z),Q(x,y,z),R(x,y,z)) ; (x,y,z)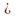 Г.

Определение. Криволинейным интегралом 2-го рода от векторного поля а по кривой Г

называется интеграл следующего вида: .

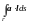Таким образом, формально, криволинейные интегралы 2-го рода сводятся к криволинейным интегралам 1-го рода специального вида. Тем самым, условия существования и общие свойства

интегралов 2-рода совпадают соответствующими условиями и свойствами интегралов 1-го рода.

Однако, имеют место и принципиальные отличия между ними:

Теорема. При изменении направления пути интегрирования криволинейные интегралы 2-го рода

меняют знак.

{Доказательство теоремы следует из того, что при изменении направления пути интегрирования вектор касательной l меняет направление на противоположное, а, значит, подынтегральная функция, а с ней и сам интеграл, меняют свой знак}

Физический смысл – работа силы а по перемещению материальной точки вдоль кривой Г.

Из представлений вектора l следует различная форма записи криволинейных интегралов 2-го рода:

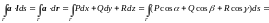
Замечания:

1). В плоском случае векторное поле а = (P(x,y),Q(x,y)); Если, кроме того, кривая задана явно, т.е.

Г: у = у(х), то

2) Криволинейные интегралы 2-го рода представляют собой сумму 3-х интегралов, каждый из которых берется от проекции векторного поля а на соответствующую координатную ось.

3) В случае кусочно-гладкой кривой нужно взять сумму интегралов по каждой из гладких частей.

П ример. где 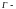дуга ОА: О(0,0), А(1,1) (рассмотреть 3 случая).

1)

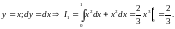
2)

3)

§4. Криволинейные интегралы по замкнутому контуру. Формула Грина.

В этом параграфе мы будем рассматривать непрерывные плоские кусочно-гладкие замкнутые кривые без точек самопересечения. Кривые остаются ориентированными, если задано положительное направление обхода: обход называется положительным, если область D, ограниченная кривой Г

остается слева (движение против часовой стрелки). Можно вычислять криволинейные интегралы

по таким кривым. При этом, начальной точкой (при t = α) может считаться любая точка кривой, а конечная (при t = β) c ней совпадает. Расчет криволинейных интегралов 1-го рода для замкнутых кривых, очевидно, ничем не отличается от общего случая, а для криволинейных интегралов 2-го рода имеет место очень важная

Теорема (формула) Грина. Пусть векторное поле а = (Р(х,у),Q(x,y)) непрерывно в 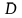и дифференцируемо в D, а Г - положительно ориентированная замкнутая кривая. В этом случае верна формула:

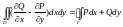. (формула Грина)

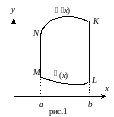
{ Пусть область D = MNKL правильная по у (рис.1).

Рассмотрим

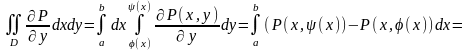
Интегралы по NM и LK равны нулю.

Аналогично: . Складывая эти результаты, получаем формулу Грина.

Разбивая исходную область на сумму правильных, получим окончательный результат.}

Определение. Криволинейные интегралы 2-го рода по замкнутому контуру называют циркуляцией векторного поля по замкнутому контуру.