Глава II. Криволинейные интегралы и теория поля.

§1. Скалярные и векторные поля.

Функцию u=u(x,y,z), заданную на множестве G в пространстве будем называть скалярным полем,

заданным на этом множестве. Векторную функцию a = (P(x,y,z),Q(x,y,z),R(x,y,z)) будем называть

векторным полем (также заданным на множестве G).

Пусть скалярное поле u дифференцируемо в области G. Тогда ему можно поставить в соответствие

векторное поле: 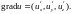Как известно, уравнение касательной плоскости к поверхности

уровня функции u (т.е. к поверхности, задаваемой уравнением u = const) имеет вид:

(все значения частных производных берутся в т. (x₀,y₀,z₀)).

Следовательно, градиент скалярного поля ортогонален к поверхности уровня в данной точке,

указывая, тем самым, направление максимального роста скалярного поля. Скорость этого роста равна

модулю (длине) вектора градиента.

Если обозначить векторное поле градиента: g = gradu, то говорят, что функция u есть потенциальная

функция (или потенциал) векторного поля g.

Линия, вектор касательной к которой в каждой точке коллинеарен вектору а в этой точке называется векторной линией поля а. Так как вектор касательной пропорционален вектору (dx,dy,dz), то для нахождения векторных линий получаем систему дифференциальных уравнений:

Если поле а является градиентом потенциала u(x, y, z), то его векторные линии ортогональны

поверхностям уровня этого потенциала : u(x, y, z) = C.

Общий пример будет рассмотрен в пятом параграфе.

§2. Криволинейные интегралы 1-го рода.

Пусть в пространстве задана спрямляемая кривая Г={x=x(t),y=y(t),z=z(t); α ≤ t ≤ β} или в векторной форме Г: r(t)=(x(t),y(t),z(t)); α ≤ t ≤ β. Кривая называется ориентированной, если т.А(х(α),у(α),z(α)) считается начальной, а В(х(β),у(β),z(β)) – конечной. ( т.е. на кривой задано положительное направление движения). В дальнейшем, по умолчанию, будем считать, что кривая Г - спрямляемая

и ориентированная. Т.е. параметр t всегда меняется от меньшего значения к большему (dt > 0).

Обозначим буквой s длину дуги кривой. Тогда элемент длины дуги равен .

( на плоскости: 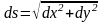или, в случае явного задания, )

Пусть функция f (x,y,z) определена на кривой Г.

Определение. Криволинейным интегралом 1-го рода называется интеграл

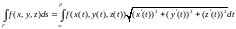
Теорема существования. Если функция f(x,y,z) непрерывна на кривой Г, то криволинейный

интеграл 1-го рода существует (от этой функции по данной кривой).

Все свойства определенных интегралов (Гл.1,§4) без изменений переносятся на криволинейные интегралы 1-го рода.

Теорема. Криволинейные интегралы 1-го рода не зависят от направления пути интегрирования.

{ Введем обозначение: f (x(t),y(t),z(t))=f ^*(t). Пусть т.(x,y,z) перемещается от т.В к т.А. Так как t может меняться только от α к β, то получаем интеграл :

т.е. получаем исходный криволинейный интеграл 1-го рода}

Приложения.

1) − длина кривой.

2) − масса кривой с линейной плотностью μ(x,y,z).

Пример. Найти массу однородной кривой : x=aּcost, y=aּsint, z=bt ; 0 ≤ t ≤ 3.

{ }