§11. Переход к цилиндрическим и сферическим координатам.

При замене переменных в пространстве наиболее часто используются две системы координат.

1. Цилиндрические координаты.

На плоскости XOY вводятся полярные координаты, а третья координата остается без изменения:

Пример. Вычислить объем тела, ограниченного поверхностями:

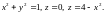
2. Сферические координаты.

Пример. Вычислить объем тела, ограниченного поверхностями:

§12. Приложения кратных интегралов.

1. Геометрические приложения двойных интегралов.

1) − площадь плоской области D.

Пример. Вычислить площадь эллипса: x²/a² + y²/b² = 1. {S = πab }

Указание: перейти к обобщенной полярной системе координат: x = aρcosφ, y = bρsinφ; J = abρ.

2) - объем цилиндра с основанием D (на плоскости XOY), образующей

параллельной оси OZ и ограниченного сверху поверхностью .

3) Площадь поверхности.

Пусть некоторая поверхность Р описывается уравнением , где D – ограниченная область плоскости с кусочно-гладкой границей, а функция имеет

непрерывные частные производные на

Формула для вычисления площади поверхности имеет вид: { Разрежем область D на частичные (см.§1) области D_i и возьмем на каждой из них произвольную

т.(x_i,y_i). На поверхности Р им будут соответствовать частичная поверхность Р_i и т.ζ_i(x_i,y_i,z_i).

Построим касательную плоскость в т.ζ_i. Вертикальный цилиндр с основанием D_i вырежет на

касательной плоскости область K_i . Предел суммы площадей K_i при стремлении к нулю

диаметров областей D_i принимается (по определению) за площадь поверхности Р. Из уравнения

касательной плоскости: p_i(X-x_i)+q_i(Y-y_i) – (Z-z_i)=0 следует, что нормаль n_i=(p_i,q_i,-1) , а направляющий косинус к оси OZ : cosγ_i=1/ . Так как площадь S(D_i)=S(K_i)cosγ_i ,

то элемент площади поверхности Р будет равен : dxdy. Отсюда и получается указанная формула}

2. Приложения тройных интегралов.

1) − объем тела Т.

2) − масса тела Т с переменной плотностью μ(x,y,z).

3) − статический момент относительно плоскости YOZ.

Аналогично вычисляются статические моменты M_xoy и M_xoz .

4) - координаты центра масс.

5) Моменты инерции относительно координатных плоскостей, координатных осей и

начала координат вычисляются по формуле: ,

r ² – квадрат расстояния от т.(x,y,z) до плоскости, оси или начала координат соответственно.

Например, r² =x², y²+z², x²+y²+z² для плоскости YOZ, оси OX и т. О.

Пример. Найти момент инерции тела с плотностью относительно оси OZ (I_OZ),

ограниченного поверхностями: x²+y²+z²=2, .(рисунок)

{ В сферической системе координат получаем:

}

§13. Несобственные кратные интегралы.

По аналогии с обычными интегралами можно ввести понятие несобственного кратного интеграла.

При этом так же рассматриваются интегралы по неограниченной области и интегралы от функций,

имеющих бесконечные разрывы как в изолированных точках, так и на отдельных кривых области D.

В первом случае рассматривается круг K_R радиуса R с центром в начале координат и пересечение

этого круга с областью D: P_R=K_R∩D. Несобственным интегралом 1-го рода по области D называется

Несобственный интеграл называется сходящимся, если этот предел существует и конечен.

В противном случае он называется расходящимся.

Во втором случае для простоты будем считать, что в области D есть одна изолированная особая

точка. Возьмем теперь круг с центром в этой точке радиуса ε: K_ε. Несобственный интеграл 2-го рода

определяется следующим образом:

Как и в случае однократного интеграла определяются понятия абсолютной и условной сходимости:

Интеграл называется абсолютно сходящимся, если сходится интеграл от модуля функции и условно

сходящимся, если сам интеграл сходится, а интеграл от модуля – расходится.

Условная сходимость обеспечивается, очевидно, переменами знака подынтегральной функции.

Верна теорема: Если интеграл сходится абсолютно, то он сходится.

{Доказательство полностью совпадает с доказательством для однократного интеграла}