§6. Переход к полярной системе координат.

Одним из наиболее важных частных случаев является полярная система координат:

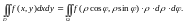
Замечания.

1. Иногда угол φ удобнее изменять в пределах от −π до π.

2. При расстановке пределов в полярных координатах ρ всегда считают внутренней переменной,

а φ − внешней.

3. Полярной системой координат удобно пользоваться, если область интегрирования является кругом, либо его частью. В случае эллиптической области выгоднее использовать обобщенные полярные координаты :

§7. Определение и теорема существования тройного интеграла.

Определение, существование и свойства тройного интеграла почти дословно повторяют соответствующие пункты для двойных интегралов. Поэтому изложение тройных интегралов будет проведено в более сжатой форме.

Рассматривается функция f (x,y,z) , определенная в некоторой ограниченной связной области Т.

Область Т разбивается на n частичных областей и в каждой из них выбирается произвольная точка 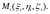Как и в случае двойного интеграла обозначим максимальный диаметр частичных областей буквой d и перейдем к пределу при в интегральной сумме.

Если этот предел существует и конечен, то он называется тройным интегралом по области Т, а сама функция f (x, y, z) интегрируемой в этой области:

объем тела .

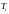Ясно, что объем тела , а масса тела с плотностью μ.

Теорема существования тройного интеграла (достаточное условие интегрируемости).

Функция, непрерывная в ограниченной замкнутой области, интегрируема в этой области.

§8. Свойства тройных интегралов.

1. Линейность.

2. Аддитивность. Пусть область Т разбита на две не имеющие общих внутренних точек области Т₁ и Т₂ . В этом случае:

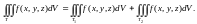
3. Интегрирование неравенств. Пусть функции интегрируемы по области Т и тогда

Следствие: теорема об оценке интеграла.

Пусть .

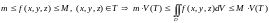4. Интегрируемость модуля. Пусть функция интегрируема на Т , тогда интегрируем на Т , причем

5. Теорема о среднем. Пусть функция непрерывна в замкнутой области . Тогда найдется т. такая, что

§9. Сведение тройного интеграла к повторному.

Тройной интеграл можно сводить к повторному двумя способами. Окончательный результат при этом, естественно, будет одним и тем же.

В первом случае тройной интеграл записывается следующим образом: Здесь D − проекция тела Т на плоскость XOY, а функции поверхности, ограничивающие тело снизу и сверху (считаем, что область Т − правильная относительно оси OZ).

Второе представление имеет вид: 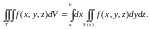В правой части равенства

a и b − наименьшая и наибольшая абсциссы проекции Т на плоскость XOY, а S(x) − сечения области Т плоскостями, параллельными плоскости YOZ и проходящими через точки

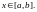
И в том и в другом случае мы имеем следующий результат:

§10. Замена переменных в тройных интегралах.

В тройных интегралах замена переменных проводится по тем же правилам, что и в двойных интегралах. Пусть это преобразование переводит область пространства UVW

в область T пространства XYZ . Формула замены переменных имеет вид:

(J − якобиан преобразования)