
- •Глава I. Кратные интегралы.
- •§1. Задачи, приводящие к кратным интегралам.
- •§2. Определение двойного интеграла. Теоремы существования.
- •§3. Основные свойства двойных интегралов.
- •§4. Вычисление двойного интеграла (переход к повторному).
- •§5. Замена переменных в двойных интегралах.
- •§6. Переход к полярной системе координат.
- •§7. Определение и теорема существования тройного интеграла.
- •§8. Свойства тройных интегралов.
- •§9. Сведение тройного интеграла к повторному.
- •§10. Замена переменных в тройных интегралах.
- •§11. Переход к цилиндрическим и сферическим координатам.
- •§12. Приложения кратных интегралов.
- •§13. Несобственные кратные интегралы.
- •Глава II. Криволинейные интегралы и теория поля.
- •§1. Скалярные и векторные поля.
- •§2. Криволинейные интегралы 1-го рода.
- •§3. Криволинейные интегралы 2-го рода.
- •§4. Криволинейные интегралы по замкнутому контуру. Формула Грина.
- •§5. Условия независимости криволинейных интегралов 2-го рода от пути интегрирования.
- •§6. Элементы теории поверхностей.
- •§7. Поверхностные интегралы 1-го рода.
- •§8. Поверхностные интегралы 2-го рода.
- •§9. Теорема (формула) Гаусса – Остроградского.
- •§10. Операторы векторного анализа (теории поля).
- •Градиент скалярного поля.
- •Дивергенция векторного поля.
- •3. Ротор ( вихрь) векторного поля.
- •§11. Теорема (формула) Стокса.
- •§12. Потенциальные и соленоидальные векторные поля.
- •§13. Повторные операции теории поля. Гармонические функции.
- •Необходимое условие сходимости ряда.
- •Достаточные признаки сходимости знакоположительного ряда.
- •Необходимое и достаточное условие сходимости знакоположительного числового ряда.
- •Первый, второй и третий признаки сравнения.
- •Признак Даламбера.
- •Радикальный признак Коши.
§4. Вычисление двойного интеграла (переход к повторному).
Рассмотрим
ограниченную замкнутую область D
, обладающую следующим свойством: любая
прямая
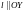 пересекает
ее границу не более, чем в двух точках.
Такие области будем называть ‘правильными’
относительно оси OY
(аналогично по оси OX).
На рис.3: D1
− ‘правильная’ по обеим осям, D2
− ‘неправильная’ по оси OY
и
‘правильная’ по оси OX.
Обозначим через a
и b
, соответственно, наименьшую и наибольшую
абсциссы области D
. Пусть
пересекает
ее границу не более, чем в двух точках.
Такие области будем называть ‘правильными’
относительно оси OY
(аналогично по оси OX).
На рис.3: D1
− ‘правильная’ по обеим осям, D2
− ‘неправильная’ по оси OY
и
‘правильная’ по оси OX.
Обозначим через a
и b
, соответственно, наименьшую и наибольшую
абсциссы области D
. Пусть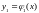 и
и
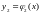 нижняя и верхняя границы области D
(рис.4).
нижняя и верхняя границы области D
(рис.4).
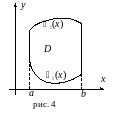
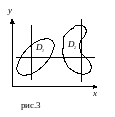
Теорема.
Пусть
функция
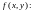
1)интегрируема по области D;
2)
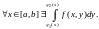
В
этом случае функция
 интегрируема по х
на
отрезке [a,b],
причем
интегрируема по х
на
отрезке [a,b],
причем
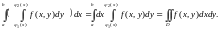
{
Зафиксируем
произвольное значение
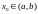 и проведем
и проведем
сечение цилиндра плоскостью, параллельной оси OZ, проходящей
через
прямую
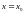 . Пусть
. Пусть
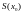 −
площадь сечения.
−
площадь сечения.
Тогда
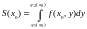 и по условию этот интеграл существует.
Объем цилиндра по площадям поперечных
сечений равен
и по условию этот интеграл существует.
Объем цилиндра по площадям поперечных
сечений равен
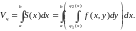 Так как он равен двойному интегралу от
функции f(x,y)
по области D,
то получаем наше утверждение.}
Так как он равен двойному интегралу от
функции f(x,y)
по области D,
то получаем наше утверждение.}
Рассмотренное представление интеграла называют переходом к повторному. В таком представлении числа а и b называют внешними пределами, а х – внешней переменной.
С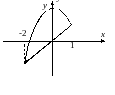 оответственно,
пределы
оответственно,
пределы
 и
переменную у
– внутренними.
и
переменную у
– внутренними.
НЕОБХОДИМЫЕ ПРИЗНАКИ ПРАВИЛЬНО РАССТАВЛЕННЫХ ПРЕДЕЛОВ:
Внешние пределы всегда постоянны.
Внутренние пределы постоянны только для координатного прямоугольника.
Внутренние пределы могут зависеть только от внешней переменной.
Если верхняя или нижняя граница не записывается одной формулой, то двойной интеграл нельзя представить в виде одного повторного с внешней переменной х. Аналогичное утверждение имеет место для левой или правой границы и внешней переменной у.
§5. Замена переменных в двойных интегралах.
Ограничимся геометрическим обоснованием формулы замены переменных в двойном интеграле.
Вспомним сначала геометрический смысл замены переменной в однократном интеграле:
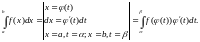 На
плоскости XOY
(т.е. в исходном интеграле) величина
dx
– элемент длины основания ступенчатой
фигуры. На плоскости TOX
при разбиении отрезка
На
плоскости XOY
(т.е. в исходном интеграле) величина
dx
– элемент длины основания ступенчатой
фигуры. На плоскости TOX
при разбиении отрезка
 элементу длины dx
соответствует величина
элементу длины dx
соответствует величина
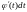 .
.
Рассмотрим
теперь двойной интеграл по области D
и
перейдем на плоскость
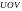 ,
сделав невырожденное преобразование
,
сделав невырожденное преобразование

(указанное
преобразование переводит область
 в область
D).
в область
D).
Произведение dxdy представляет собой элемент площади основания цилиндра – прямоугольник в
области D. В области ему соответствует криволинейный ‘параллелограмм’, площадь которого
(с точностью до бесконечно малых более высокого порядка малости) равна площади
параллелограмма,
построенного на векторах, касательных
к его сторонам (рис.5). В свою очередь,
этими касательными являются векторы
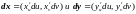 ,
а площадь параллелограмма – модулю их
векторного произведения (см. курс
аналитической геометрии) :
,
а площадь параллелограмма – модулю их
векторного произведения (см. курс
аналитической геометрии) :
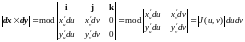 ;
(
;
(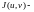 якобиан преобразования). Таким образом,
окончательно имеем:
якобиан преобразования). Таким образом,
окончательно имеем:
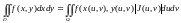 −
формула
замены переменных в двойных интегралах.
−
формула
замены переменных в двойных интегралах.
