Признак Даламбера.

Пусть - знакоположительный числовой ряд. Если , то числовой ряд сходится, если , то ряд расходится.

Замечание.

Признак Даламбера справедлив, если предел бесконечен, то есть, если , то ряд сходится, если , то ряд расходится.

Если , то признак Даламбера не дает информацию о сходимости или расходимости ряда и требуется дополнительное исследование.

Радикальный признак Коши.

Пусть - знакоположительный числовой ряд. Если , то числовой ряд сходится, если , то ряд расходится.

Замечание.

Радикальный признак Коши справедлив, если предел бесконечен, то есть, если , то ряд сходится, если , то ряд расходится.

Если , то радикальный признак Коши не дает информацию о сходимости или расходимости ряда и требуется дополнительное исследование.

Обычно достаточно легко разглядеть случаи, когда лучше всего использовать радикальный признак Коши. Характерным является случай, когда общий член числового ряда представляет собой показательно степенное выражение. Рассмотрим несколько примеров.

Интегральный признак Коши.

Пусть - знакоположительный числовой ряд. Составим функцию непрерывного аргумента y = f(x), аналогичную функции . Пусть функция y = f(x) положительная, непрерывная и убывающая на интервале , где ). Тогда в случае сходимости несобственного интеграла 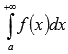сходится исследуемый числовой ряд. Если же несобственный интеграл расходится, то исходный ряд тоже расходится.

Исследование знакопеременных рядов на абсолютную сходимость.

Проще всего исследовать знакопеременный числовой ряд на абсолютную сходимость. В этом случае берем знакоположительный ряд , составленный из абсолютных величин членов исходного ряда, и применяем к нему подходящий достаточный признак сходимости из рассмотренных выше. Если ряд сходится, то исходный ряд является абсолютно сходящимся.

Расходимость знакопеременных рядов.

Если ряд расходится, то соответствующий знакопеременный ряд может, либо расходится, либо сходится условно.

Только признак Даламбера и радикальный признак Коши позволяют сделать вывод о расходимости знакопеременного ряда по расходимости ряда из модулей . Ряд также расходится, если не выполняется необходимое условие сходимости, то есть, если .

Достаточные признаки условной сходимости числового ряда.

Признак Лейбница.

Если абсолютные величины членов знакочередующегося ряда монотонно убывают и предел модуля общего члена ряда равен нулю при , то ряд сходится.