§13. Повторные операции теории поля. Гармонические функции.

В физике векторных полей часто встречаются ситуации, когда один из операторов поля действует

на результат действия другого (или того же) оператора. Рассмотрим, предварительно, еще один оператор, действующий как на скалярные, так и на векторные функции.

Определение. Оператором Лапласа ∆ называется оператор:

.

Оператор Лапласа легко выражается через оператор набла:

Перейдем теперь к повторным операторам.

1.

{ Это равенство: 1) получается непосредственным вычислением, 2)следует из теоремы 1 §12 и 3) из

символической записи: }

2.

{ В символической записи = 0: смешанное произведение компланарных векторов}

3. 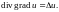{ Непосредственное вычисление }

4. . { Непосредственное вычисление }

В волновых процессах очень большую роль играет уравнение Лапласа:

Определение. Функции, удовлетворяющие уравнению Лапласа, называются гармоническими.

Пример. u = x² – y² +z − гармоническая.

Свойства сходящихся числовых рядов.

1. Если сходится числовой ряд 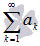, то сходящимся будет и ряд 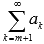. Другими словами, сходящимся будет и ряд без первых m членов. Если к сходящемуся числовому ряду добавить несколько членов (от первого до m-ого), то полученный ряд также будет сходящимся.

2. Если сходится числовой ряд и его сумма равна S, то сходящимся будет и ряд 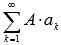, причем 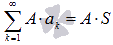, где A – произвольная постоянная.

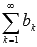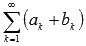3. Если сходятся числовые ряды и , их суммы равны A и B соответственно, то сходящимися будут ряды и , причем их суммы будут равны A + B и A - B соответственно.

Необходимое условие сходимости ряда.

Если числовой ряд сходится, то предел его k-ого члена равен нулю: .

При исследовании любого числового ряда на сходимость в первую очередь следует проверять выполнение необходимого условия сходимости. Невыполнение этого условия указывает на расходимость числового ряда, то есть, если , то ряд расходится.

С другой стороны нужно понимать, что это условие не является достаточным. То есть, выполнение равенства не говорит о сходимости числового ряда . К примеру, для гармонического ряда необходимое условие сходимости выполняется , а ряд расходится.

Достаточные признаки сходимости знакоположительного ряда.

При использовании достаточных признаков для исследования числовых рядов на сходимость постоянно приходится сталкиваться с вычислением пределов, так что рекомендуем обращаться к этому разделу при затруднениях.

Необходимое и достаточное условие сходимости знакоположительного числового ряда.

Для сходимости знакоположительного числового ряда необходимо и достаточно, чтобы последовательность его частичных сумм была ограничена.

Начнем с признаков сравнения рядов. Их суть заключается в сравнении исследуемого числового ряда с рядом, сходимость или расходимость которого известна.

Первый, второй и третий признаки сравнения.

Первый признак сравнения рядов.

Пусть и - два знакоположительных числовых ряда и выполняется неравенство для всех k = 1, 2, 3, ... Тогда из сходимости ряда следует сходимость , а из расходимости ряда следует расходимость .

Первый признак сравнения используется очень часто и представляет собой очень мощный инструмент исследования числовых рядов на сходимость. Основную проблему представляет подбор подходящего ряда для сравнения. Ряд для сравнения обычно (но не всегда) выбирается так, что показатель степени его k-ого члена равен разности показателей степени числителя и знаменателя k-ого члена исследуемого числового ряда. К примеру, пусть , разность показателей степени числителя и знаменателя равна 2 – 3 = -1, поэтому, для сравнения выбираем ряд с k-ым членом , то есть, гармонический ряд. Рассмотрим несколько примеров.

Второй признак сравнения.

Пусть и - знакоположительные числовые ряды. Если , то из сходимости ряда следует сходимость . Если , то из расходимости числового ряда следует расходимость .

Следствие.

Если и , то из сходимости одного ряда следует сходимость другого, а из расходимости следует расходимость.

Исследуем ряд на сходимость с помощью второго признака сравнения. В качестве ряда возьмем сходящийся ряд . Найдем предел отношения k-ых членов числовых рядов:

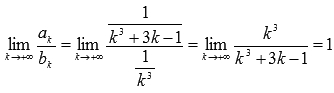
Таким образом, по второму признаку сравнения из сходимости числового ряда следует сходимость исходного ряда.

Третий признак сравнения.

Пусть и - знакоположительные числовые ряды. Если с некоторого номера N выполняется условие , то из сходимости ряда следует сходимость , а из расходимости ряда следует расходимость .

К началу страницы