
- •Глава I. Кратные интегралы.
- •§1. Задачи, приводящие к кратным интегралам.
- •§2. Определение двойного интеграла. Теоремы существования.
- •§3. Основные свойства двойных интегралов.
- •§4. Вычисление двойного интеграла (переход к повторному).
- •§5. Замена переменных в двойных интегралах.
- •§6. Переход к полярной системе координат.
- •§7. Определение и теорема существования тройного интеграла.
- •§8. Свойства тройных интегралов.
- •§9. Сведение тройного интеграла к повторному.
- •§10. Замена переменных в тройных интегралах.
- •§11. Переход к цилиндрическим и сферическим координатам.
- •§12. Приложения кратных интегралов.
- •§13. Несобственные кратные интегралы.
- •Глава II. Криволинейные интегралы и теория поля.
- •§1. Скалярные и векторные поля.
- •§2. Криволинейные интегралы 1-го рода.
- •§3. Криволинейные интегралы 2-го рода.
- •§4. Криволинейные интегралы по замкнутому контуру. Формула Грина.
- •§5. Условия независимости криволинейных интегралов 2-го рода от пути интегрирования.
- •§6. Элементы теории поверхностей.
- •§7. Поверхностные интегралы 1-го рода.
- •§8. Поверхностные интегралы 2-го рода.
- •§9. Теорема (формула) Гаусса – Остроградского.
- •§10. Операторы векторного анализа (теории поля).
- •Градиент скалярного поля.
- •Дивергенция векторного поля.
- •3. Ротор ( вихрь) векторного поля.
- •§11. Теорема (формула) Стокса.
- •§12. Потенциальные и соленоидальные векторные поля.
- •§13. Повторные операции теории поля. Гармонические функции.
- •Необходимое условие сходимости ряда.
- •Достаточные признаки сходимости знакоположительного ряда.
- •Необходимое и достаточное условие сходимости знакоположительного числового ряда.
- •Первый, второй и третий признаки сравнения.
- •Признак Даламбера.
- •Радикальный признак Коши.
Глава I. Кратные интегралы.
§1. Задачи, приводящие к кратным интегралам.
К определению двойного интеграла приводит задача вычисления объема прямого цилиндра с плоским основанием, ограниченного сверху некоторой поверхностью. К тройному интегралу приводит задача вычисления массы тела с переменной плотностью. Обе задачи решаются по аналогии с вычислением площади криволинейной трапеции с помощью интегрального исчисления. Так, например, при вычислении объема указанного цилиндра его основание разбивается на множество маленьких областей. Объем каждого цилиндра, построенного на таких областях, близок к объему обычного цилиндра с высотой, равной значению функции, описывающей накрывающую поверхность, в некоторой точке этой частичной области. Объем всего цилиндра близок, таким образом, к сумме объемов всех таких цилиндров. Аналогично решается задача вычисления массы некоторого тела в трехмерном пространстве.
§2. Определение двойного интеграла. Теоремы существования.
Рассматривается
прямой цилиндр, основанием которого
является замкнутая область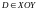 ,
ограниченный сверху поверхностью
,
ограниченный сверху поверхностью
 .
Основание D
разбивается на частичные области
.
Основание D
разбивается на частичные области
 таким образом, что
таким образом, что
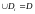 ,
а пересечениями могут быть только их
границы (рис.1). В каждой частичной области
выбирается произвольная т.
,
а пересечениями могут быть только их
границы (рис.1). В каждой частичной области
выбирается произвольная т.
 .
Рассматривается интегральная
сумма
для функции f
(x,y)
по области D:
.
Рассматривается интегральная
сумма
для функции f
(x,y)
по области D:
 площадь
частичной области
.
площадь
частичной области
.
Определение.
Пусть
 − диаметр области
и
− диаметр области
и
 Если
Если

существует
конечный предел интегральных сумм при
 ,
не зависящий от способа разбиения и
выбора точек
,
не зависящий от способа разбиения и
выбора точек
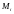 , то этот предел называется двойным
интегралом от
функции f
(x,y)
по области D,
а сама функция − интегрируемой по этой
области:
, то этот предел называется двойным
интегралом от
функции f
(x,y)
по области D,
а сама функция − интегрируемой по этой
области:
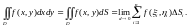
Классы интегрируемых функций двух переменных почти полностью повторяют классы интегрируемых функций одной переменной. Доказательства соответствующих теорем также полностью совпадают
Теорема 1. (Необходимое условие интегрируемости) Если функция интегрируема по области D, она ограничена в этой
области.
Теорема 2. (Основная теорема существования или достаточное условие интегрируемости) Функция, непрерывная в ограниченной замкнутой области D , интегрируема по этой области.
На самом деле, функция интегрируема при менее жестких ограничениях:
Теорема 3. Ограниченная функция, имеющая конечное число точек и линий (спрямляемых, т.е. конечной длины) разрыва в области D, интегрируема по этой области.
§3. Основные свойства двойных интегралов.
Все основные свойства двойных интегралов, практически, совпадают со свойствами однократных (включая доказательства). Отсутствует только аналог следующего свойства однократного интеграла:
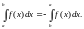 Перечислим
эти свойства:
Перечислим
эти свойства:
Линейность.
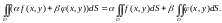
Аддитивность. Пусть область D разбита на две не имеющие общих внутренних точек области D1 и D2 . В этом случае:

Интегрирование неравенств. Пусть функции
 интегрируемы по области D
и
интегрируемы по области D
и
 тогда
тогда

Следствие: теорема об оценке интеграла.
Пусть
 .
.
Интегрируемость модуля. Пусть функция
 интегрируема на D
, тогда
интегрируема на D
, тогда
 интегрируем на D
, причем
интегрируем на D
, причем

Теорема о среднем. Пусть функция непрерывна в замкнутой области
 .
Тогда найдется т.
.
Тогда найдется т.
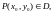 такая, что
такая, что

