Межосевое расстояние червячной передачи
a=0,5(d1+d2)=0,5m(q+z2).
В силовых червячных передачах рекомендуется принимать следующие значения числа зубьев червячного колеса.
z2>21 – при одновитковом червяке;
z2>25 – при многовитковых червяках.
Кинематика червячных передач. Выше говорилось о том, что червячное зацепление в сечении средней торцовой плоскостью колеса можно рассматривать как плоское зубчато-реечное зацепление, причем скорость v1 осевого перемещения витков червяка равна окружной скорости v2 червячного колеса на делительной окружности.
Так как за каждый оборот червяка сечение витка смещается в осевом направлении на величину хода резьбы pz=pz1, то v1=pz1n1=mz1n1; червячное колесо имеет окружную скорость v2=d2n2=mz2n2.
Так как v1=v2, то z1n1=z2n2 или z11=z22.
Следовательно, передаточное число червячной передачи
i=1/2=n1/n2=z2/z1.
Передаточное число червячной передачи равно отношению числа зубьев червячного колеса к числу витков червяка.
В силовых передачах, в частности в стандартных передачах редукторов, передаточные числа принимают в пределах i=8...80.
Основные параметры (межосевые расстояния а, номинальные передаточные числа i, сочетания модулей т, коэффициентов диаметра червяка q и чисел витков z1) цилиндрических червячных передач для редукторов регламентированы ГОСТом. Указанный стандарт предусматривает применение одно-, двух и четырехвитковых червяков, обычно с линией витков правого направления, наименьшее число зубьев червячного колеса, предусмотренное стандартом, z2=32.
Основные параметры (межосевые расстояния, номинальные передаточные числа, делительные диаметры червяков и ширины венцов червячных колес) глобоидных передач для редукторов также установлены ГОСТом.
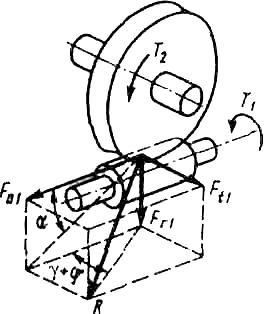
Сила R взаимодействия витка червяка и зуба червячного колеса (равная векторной сумме силы нормального давления и силы трения) будет отклоняться от средней плоскости червячного колеса на угол + ', где – угол подъема линии витка; ' – приведенный угол трения.
Разложив силу R на три взаимно перпендикулярные составляющие по реальным направлениям, получим (рис. 127):
окружная сила на червяке, численно равная осевой силе на червячном колесе, Ft1 =2T1/d1=Fa2;
осевая сила на червяке, численно равная окружной силе на червячном колесе,
Ft2 =2T2/d2=Fa1;
радиальная сила на червяке и червячном колесе
Fr1=Fr2=Fa1tg.
|
Рис. 127 |
В приведенных формулах Т1, Т2 – крутящие моменты на валу червяка и червячного колеса; d1, d2 – диаметры делительных цилиндров червяка и червячного колеса; – угол профиля витка червяка в осевом сечении.
Крутящие моменты на валах червяка и червячного колеса связаны зависимостью
T1=T2i,
где – КПД передачи; i – передаточное число.
Коэффициент полезного действия червячной передачи определяется потерями на трение в зацеплении, потерями на перемешивание и разбрызгивание масла и потерями в опорах валов, причем в червячных передачах последние два вида потерь отдельно не учитываются, так как они относительно невелики и зафиксированы при экспериментальном определении значений '.
Потери на трение в червячном зацеплении определяются так же, как в винтовой паре, поэтому КПД червячной передачи при ведущем червяке определяется по формуле
=tg/tg(+ '),
где – угол подъема линии витка; ' – приведенный угол трения.
Так как возрастает с увеличением угла , то КПД червячных передач повышается с увеличением числа витков червяка.
При проектных расчетах, когда элементы конструкции и размеры червяка и червячного колеса еще неизвестны, ориентировочно можно принимать следующие значения КПД: при z1=1 =0,7...0,75; при z1=2 =0,75...0,82; при z3=1 =0,82...0,87; при z1=4 =0,87...0,92.