Коэффициент осевого перекрытия косозубой передачи

_=b/p_x,

где b – ширина венца; р_х – осевой шаг.

Нетрудно показать, что если _ – целое число, то суммарная длина контактных линий будет все время оставаться постоянной, что благоприятно для работы передачи, так как нагрузка на зубья в процессе зацепления будет оставаться постоянной, а шум и динамические нагрузки уменьшатся.

Силу нормального давления F_n в зацеплении косозубых колес можно разложить на три взаимно перпендикулярные составляющие: окружную силу F_t, радиальную силу F_r, и осевую силу F_a, равные:

F_t=2T/d; F_r=F_ttg/cos; F_a=F_ttg,

где Т – передаваемый крутящий момент;  – угол зацепления.

Наличие осевой силы – существенный недостаток косозубых передач. Во избежание больших осевых сил в косозубой передаче угол наклона линии зуба ограничивают значениями =8...20°, несмотря на то, что с увеличением  увеличивается прочность зубьев, плавность работы передачи, ее нагрузочная способность.

В современных передачах косозубые колеса имеют преимущественное распространение.

В отличие от косозубой в винтовой зубчатой передаче между зубьями возникает не линейный, а точечный контакт, что значительно увеличивает контактные напряжения и снижает нагрузочную

Рис. 106

способность передачи. Кроме того, в винтовой зубчатой передаче значи-тельной величины дости-гает относительное сколь-жение зубьев, что сущест-венно снижает ее КПД, создает склонность к зае-данию и вызывает быст-рый износ зубьев. Учиты-вая эти недостатки. винто-вые зубчатые передачи не следует применять в качестве силовых передач.

Обязательное условие для винтовой зубчатой передачи – равенство нормальных модулей. Углы наклона линии зуба ведущего и ведомого колес могут быть различными и угол скрещивания осей может быть не равен 90°.

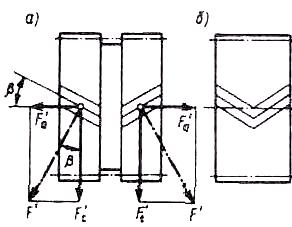
Цилиндрическое зубчатое колесо, венец которого по ширине состоит из участков с правыми и левыми зубьями, называется шевронным. Часть венца с зубьями одинакового направления называется полушевроном. Из технологических соображений шевронные колеса изготовляют двух типов (рис. 106): с дорожкой посредине колеса (а) и без дорожки (б). В шевронном колесе осевые силы F_a на полушевронах, направленные в противоположные стороны, взаимно уравновешиваются внутри колеса и на валы и опоры валов не передаются. Поэтому у шевронных колес угол наклона зубьев принимают в пределах =25...40°, в результате чего повышается прочность зубьев, плавность работы передачи и ее нагрузочная способность. Шевронные колеса применяют в мощных быстроходных закрытых передачах. Недостатком шевронных колес является высокая трудоемкость и себестоимость изготовления.

Геометрические, кинематические и прочностные расчеты шевронной и косозубой передач аналогичны.

Конические зубчатые передачи

Конические зубчатые передачи применяют при пересекающихся (рис. 100, д, е, ж) или скрещивающихся осях (гипоидная передача на рис. 100, з). Межосевой угол  может изменяться в широком диапазоне значений (10°<<170°), но наибольшее распространение имеют ортогональные конические передачи с углом =90°.

Конические зубчатые передачи по сравнению с цилиндрическими имеют большую массу и габариты, сложнее в изготовлении, а также монтаже, так как требуют точной фиксации осевого положения зубчатых колес.

Наибольшее распространение имеют конические передачи с прямыми и криволинейными зубьями. Конические зубчатые колеса с криволинейными зубьями могут иметь круговую, эвольвентную и циклоидальную линию зубьев; наиболее распространенные колеса с круговыми зубьями.

Конические передачи с криволинейными зубьями по сравнению с прямозубыми имеют большую нагрузочную способность, работают более плавно и, следовательно, динамические нагрузки и шум при их работе меньше. Допуски для конических и гипоидных передач регламентированы стандартом, согласно которому установлено двенадцать степеней точности и соответствующие нормы точности.

Предельные окружные скорости для конических прямозубых (непрямозубых) колес имеют следующие величины: при 6-й степени точности – до 12 (20) м/с, 7-й степени – до 8 (10) м/с, 8-й степени – до 4 (7) м/с, 9-й–до 1,5(3) м/с.

Расчет геометрии конических прямозубых передач регламентирован ГОСТом. К основным геометрическим параметрам прямозубого конического колеса относятся (рис. 107): R_e, R – внешнее и среднее конусное расстояния; b – ширина зубчатого венца; d, d, – средний и внешний делительный диаметры; d_ae, d_fe – внешние диаметры вершин зубьев и впадин;  – угол делительного конуса; h_ae, h_fe – внешняя высота делительной головки и ножки зуба; _a=_f= – угол делительной головки и ножки зуба.

Углы головки и ножки зуба сделаны одинаковыми для того, чтобы образующая конуса вершин зубьев одного колеса была параллельна образующей конуса впадины второго колеса, в результате чего радиальный зазор по длине прямого зуба будет постоянным (поэтому на рисунке вершины конусов не совпадают).

По приведенным выше параметрам определяют остальные размеры колес и передачи, в частности:

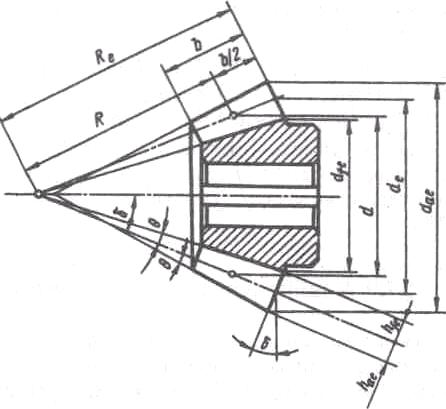
Рис. 107

угол конуса вершин зубьев

_a=+;

угол конуса впадин

_f=–;

межосевой угол передачи

=₁+₂.

У конических колес высота, толщина зубьев и окружной шаг по длине зуба неодинаковы, поэтому различают два окружных модуля: т – средний делительный окружной модуль, причем d=mz, где z – число зубьев колеса; т_e – внешний делительный окружной модуль, причем d_e=m_ez.

Внешний и средний модули пропорциональны соответствующим конусным расстояниям, поэтому

m_e=mR_e/R.

Для удобства измерений на чертежах задают внешние размеры зубьев и колес, а модуль т_e называют производственным, который можно (но не обязательно) округлить до стандартного значения.

Профилирование зубьев конических колес с прямыми и тангенциальными, а также с круговыми зубьями ведется в соответствии со стандартами на соответствующие исходные контуры. Исходный контур для прямозубых конических колес аналогичен исходному контуру для цилиндрических колес, за исключением радиального зазора с=0,2т_e; внешняя высота головок зубьев h_ae=т_e, внешняя высота ножек h_fe=1,2т_e, а внешняя высота зуба h_a=2,2.