4. Геометрический способ сложения сил. Равнодействующая сходящихся сил

Решение многих задач механики связано с известной из векторной алгебры операцией сложения векторов и, в частности, сил. Величину, равную геометрической сумме сил какой-нибудь системы, будем в дальнейшем называть главным вектором этой системы сил. Понятие о геометрической сумме сил не следует смешивать с понятием о равнодействующей; для многих систем сил равнодействующей вообще не существует, геометрическую же сумму (главный вектор) можно вычислить для любой системы сил.

1. Сложение двух сил. Геометрическая сумма F двух сил F₁ и F₂ находится по правилу параллелограмма (рис. 4, а) или построением силового треугольника (рис. 4, б), изображающего одну из половин этого параллелограмма. Если угол между силами равен , то модуль R и углы , , которые сила R образует со слагаемыми силами, определяются по формулам:

;

F₁/sin=F₂/sin=R/sin.

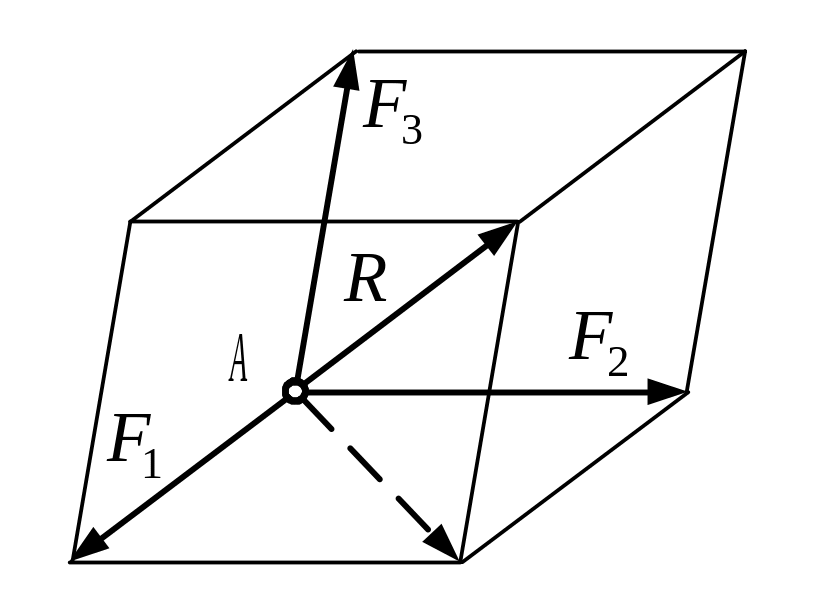
2. Сложение трех сил, не лежащих в одной плоскости. Геометрическая сумма R трех сил F₁, F₂, F₃, не лежащих в одной плоскости, изображается диагональю параллелепипеда, построенного на этих силах (правило параллелепипеда). В справедливости этого убеждаемся, применяя последовательно правило параллелограмма (рис. 5).

а	б	в
Рис. 4		Рис. 5

3. Сложение системы сил. Геометрическая сумма (главный вектор) любой системы сил определяется или последовательным сложением сил системы по правилу параллелограмма, или построением силового многоугольника. Второй способ является более простым и удобным. Для нахождения этим способом суммы сил , , , ..., , (рис. 6, а) от произвольной точки О (рис. 6, б) откладываем вектор , изображающий в выбранном масштабе силу

, от точки а – вектор , изображающий силу , от точки b – вектор , изображающий силу , и т.д.; от конца т предпоследнего вектора откладываем вектор , изображающий силу . Соединяя начало первого и
	а	б
	Рис. 6

конец последнего вектора, получаем вектор , изображающий главный вектор (геометрическую сумму) слагаемых сил:

или .

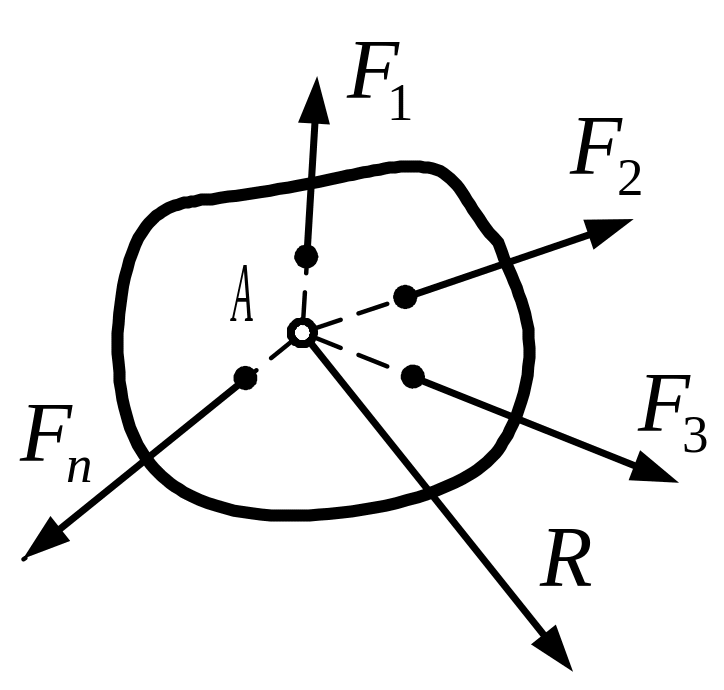
4. Равнодействующая сходящихся сил. Рассмотрим систему сходящихся сил, т.е. сил, линии действия которых пересекаются в одной точке (рис. 6, а). Так как сила, действующая на абсолютно твердое тело, является вектором скользящим, то система сходящихся сил эквивалентна системе сил, приложенных в одной точке (на рис. 6, а в точке A).

Система сходящихся сил имеет равнодействующую, равную геометрической сумме (главному вектору) этих сил и приложенную в точке пересечения их линий действия. Следовательно система сил , , ..., , изображенных на рис. 6, а, имеет равнодействующую, равную их главному вектору и приложенную в точке А (или в любой другой точке, лежащей на линии действия силы , проведенной через точку A).