7.3. Конические зубчатые передачи

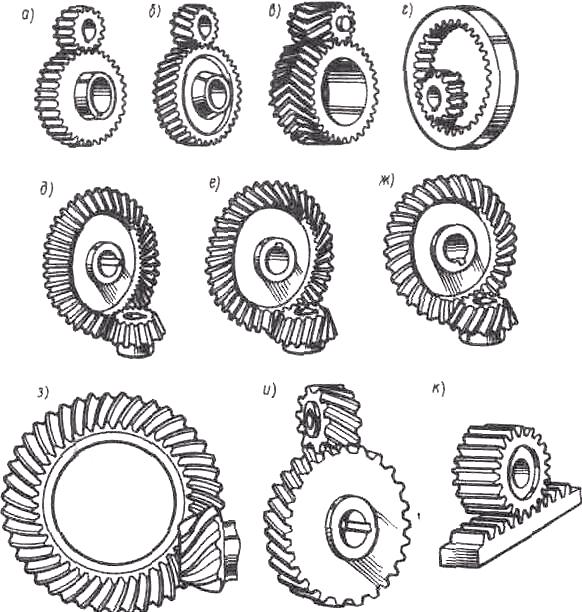
Конические зубчатые передачи применяют при пересекающихся (рис. 15, а, б, в) или скрещивающихся осях (гипоидная передача на рис. 15, г). Межосевой угол  может изменяться в широком диапазоне

а	б
в	г

Рис. 15

значений (10°<<170°), но наибольшее распространение имеют ортогональные конические передачи с углом  = 90°.

Конические зубчатые передачи по сравнению с цилиндрическими имеют большую массу и габариты, сложнее в изготовлении, а также монтаже, так как требуют точной фиксации осевого положения зубчатых колес.

Наибольшее распространение имеют конические передачи с прямыми и криволинейными зубьями. Конические зубчатые колеса с криволинейными зубьями могут иметь круговую, эвольвентную и циклоидальную линию зубьев; наиболее распространенные колеса с круговыми зубьями.

Конические передачи с криволинейными зубьями по сравнению с прямозубыми имеют большую нагрузочную способность, работают более плавно и, следовательно, динамические нагрузки и шум при их работе меньше. Допуски для конических и гипоидных передач регламентированы стандартом, согласно которому установлено двенадцать степеней точности и соответствующие нормы точности.

Предельные окружные скорости для конических прямозубых (непрямозубых) колес имеют следующие величины: при 6-й степени точности – до 12 (20) м/с, 7-й степени – до 8 (10) м/с, 8-й степени – до 4 (7) м/с, 9-й–до 1,5 (3) м/с.

Расчет геометрии конических прямозубых передач регламентирован ГОСТом. К основным геометрическим параметрам прямозубого конического колеса относятся (рис. 16): R_e, R – внешнее и среднее конусное расстояния; b – ширина зубчатого венца; d, d, – средний и внешний делительный диаметры; d_ae, d_fe – внешние диаметры вершин зубьев и впадин;  – угол делительного конуса; h_ae, h_fe – внешняя высота делительной головки и ножки зуба; _a = _f =  – угол делительной головки и ножки зуба.

Углы головки и ножки зуба сделаны одинаковыми для того, чтобы образующая конуса вершин зубьев одного колеса была параллельна образующей конуса впадины второго колеса, в результате чего радиальный зазор по длине прямого зуба будет постоянным (поэтому на рисунке вершины конусов не совпадают).

По приведенным выше параметрам определяют остальные размеры колес и передачи, в частности:

угол конуса вершин зубьев

_a = +;

угол конуса впадин

_f = –;

межосевой угол передачи

 = ₁+₂.

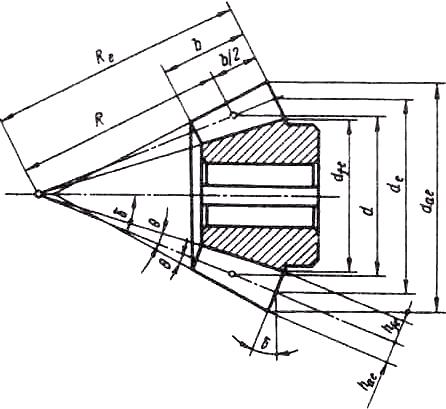
Рис. 16

У конических колес высота, толщина зубьев и окружной шаг по длине зуба неодинаковы, поэтому различают два окружных модуля: т – средний делительный окружной модуль, причем d = mz, где z – число зубьев колеса; т_e – внешний делительный окружной модуль, причем d_e = m_ez.

Внешний и средний модули пропорциональны соответствующим конусным расстояниям, поэтому

m_e = mR_e/R.

Для удобства измерений на чертежах задают внешние размеры зубьев и колес, а модуль т_e называют производственным, который можно (но не обязательно) округлить до стандартного значения.

Профилирование зубьев конических колес с прямыми и тангенциальными, а также с круговыми зубьями ведется в соответствии со стандартами на соответствующие исходные контуры. Исходный контур для прямозубых конических колес аналогичен исходному контуру для цилиндрических колес, за исключением радиального зазора с = 0,2т_e; внешняя высота головок зубьев h_ae = т_e, внешняя высота ножек h_fe = 1,2т_e, а внешняя высота зуба h_a = 2,2.

Внешний диаметр вершин зубьев равен

d_ae = d_e+2h_aecos = m_e(z+2cos).

Очевидно, что при  = 90°

а также

R_e = d_e/(2sin), R = R_e–b/2.

Углы делительных конусов ортогональных передач легко определяются в зависимости от числа зубьев ведущего и ведомого колес, а следовательно, от передаточного числа передачи:

tg₁ = d₁/d₂ = z₁/z₂ = 1/i или i = ctg₁ = tg₂.

Ширину зубчатого венца b по стандарту рекомендуется принимать

b<0,3R_e или b<10m_e;

вычисленное значение округляется до целого числа, а при проектировании стандартных редукторов значения b принимаются по стандарту.

Кроме ширины венца b, указанный стандарт на ортогональные конические передачи для редукторов устанавливает номинальные значения внешнего делительного диаметра колеса de₂ (в основном определяющего габариты редуктора) и номинальные значения передаточных чисел i (от i = 1 до i = 6,3).

Для прямозубых конических передач рекомендуется i<3, для передач с криволинейными зубьями i<6,3; число зубьев меньшего колеса рекомендуется принимать z₁ = 18...30.