Все основные параметры зубчатых колес выражают через модули, а именно: шаг зубьев

р = т;

Диаметр делительной окружности

d = mz.

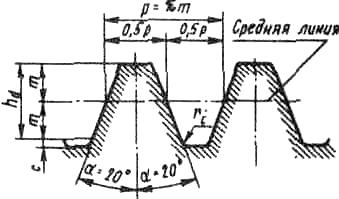
В соответствии со стандартным исходным контуром для зубчатых цилиндрических колес (рис. 11) высота головки зуба ha = m, высота ножки зуба hf = т+с = 1,25т, где с = 0,25т – радиальный зазор; в пределах глубины захода hd = 2т профиль исходного контура прямолинейный; радиус закругления у основания зуба ri = 0,25m.

Рис. 11

Высота зубьев цилиндрических колес

h = h_a+h_f = 2,25m.

Диаметр окружности вершин зубьев

d_a = d+2h_a = mz+2т = m(z+2),

диаметр окружности впадин

d_f = d–2h_f = mz–2·1,25m = m(z–2,5).

Расстояние между торцами зубьев колеса называется шириной венца.

Межосевое расстояние цилиндрической передачи с внешним и внутренним зацеплением

a = (d₁±d₂)/2 = m(z₁±z₂)/2

называется делительным межосевым расстоянием (знак минус для внутреннего зацепления). Если межосевое расстояние отличается от делительного, то оно обозначается а_w.

Рис. 12

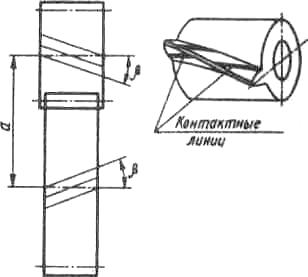
7.2. Цилиндрические косозубые и шевронные зубчатые передачи Косозубыми называют колеса, у которых теоре-тическая делительная линия зуба является частью винто-вой линии постоянного шага (теоретической делительной линией называется линия пересечения боковой по-верхности зуба с делитель-ной цилиндрической по-верхностью). Линия зуба

косозубых колес может иметь правое и левое направление винтовой линии. Угол наклона линии зуба обозначается  (рис. 12).

Косозубая передача с параллельными осями имеет противоположное направление зубьев ведущего и ведомого колес и относится к категории цилиндрических зубчатых передач, так как начальные поверхности таких зубчатых колес представляют собой боковую поверхность цилиндров. Передача с косозубыми колесами, оси которых скрещиваются, имеет одинаковое направление зубьев обоих колес и называется винтовой зубчатой передачей, которая относится к категории гиперболоидных зубчатых передач, так как начальные поверхности таких зубчатых колес являются частями однополостного гиперболоида вращения; делительные поверхности этих колес – цилиндрические.

У косозубых передач контактные линии расположены наклонно по отношению к линии зуба, поэтому в отличие от прямых косые зубья входят в зацепление не сразу по всей длине, а постепенно, что обеспечивает плавность зацепления и значительное снижение динамических нагрузок и шума при работе передачи. Поэтому косозубые передачи по сравнению с прямозубыми допускают значительно большие предельные окружные скорости колес. Так, например, косозубые колеса 6-й степени точности применяют при окружной скорости до 30 м/с; 7-й степени – до 15 м/с; 8-й степени – до 10 м/с; 9-й – до 4 м/с.

Угол перекрытия косозубого колеса состоит из угла торцового и угла осевого перекрытий, следовательно, коэффициент перекрытия _ косозубой передачи равен сумме коэффициентов торцового _ и осевого _ перекрытия

_ = _+_>2,

поэтому у косозубой передачи нет периода однопарного зацепления.

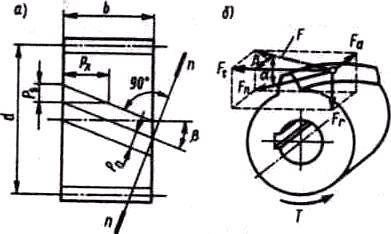
Косозубые колеса обрабатывают теми же зуборезными инструментами, что и прямозубые, поэтому стандартные параметры колес задаются в нормальном к зубу сечении пп (рис. 13). Нормальный модуль m_n = р_n/, где р_n – нормальный шаг, измеренный по делительной поверхности. Кроме нормального модуля, в косозубых колесах различают: окружной модуль т_t = р_t/п, где p_t – окружной шаг, измеряемый по дуге делительной окружности в торцовом сечении; осевой модуль т_x = p_x/, где р_х – осевой шаг, измеряемый по образующей делительного цилиндра.

Так как р_t = p_n/cos, то m_t = m_n/cos.

Размеры зубьев косозубого колеса определяют по нормальному модулю, т. е.

h = h_a+h_f = m_n+1,25m_n = 2,25m_n,

а диаметр делительной окружности колеса по окружному модулю

а

б

Рис. 13

d = m_tz = m_nz/cos.

Размеры косозубых колес и межосевое расстояние передачи определяют по следующим формулам:

диаметр вершин зубьев

d_a = d+2h_a = d+2m_n;

диаметр впадин

d_f = d–2h_f = d–2,5m_n;

межосевое расстояние

а = m_t(z₁+z₂)/2 = m_n(z₁+z₂)/(2cos).

Коэффициент осевого перекрытия косозубой передачи

_ = b/p_x,

где b – ширина венца; р_х – осевой шаг.

Нетрудно показать, что если _ – целое число, то суммарная длина контактных линий будет все время оставаться постоянной, что благоприятно для работы передачи, так как нагрузка на зубья в процессе зацепления будет оставаться постоянной, а шум и динамические нагрузки уменьшатся.

Силу нормального давления F_n в зацеплении косозубых колес можно разложить на три взаимно перпендикулярные составляющие: окружную силу F_t, радиальную силу F_r, и осевую силу F_a, равные:

F_t = 2T/d; F_r = F_ttg/cos; F_a = F_ttg,

где Т – передаваемый крутящий момент;  – угол зацепления.

Наличие осевой силы – существенный недостаток косозубых передач. Во избежание больших осевых сил в косозубой передаче угол наклона линии зуба ограничивают значениями  = 8...20°, несмотря на то, что с увеличением  увеличивается прочность зубьев, плавность работы передачи, ее нагрузочная способность.

В современных передачах косозубые колеса имеют преимущественное распространение.

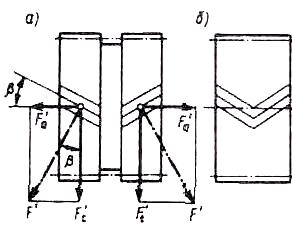
Цилиндрическое зубчатое колесо, венец которого по ширине состоит из участков с правыми и левыми зубьями, называется шевронным. Часть венца с зубьями одинакового направления называется полушевроном. Из технологических соображений шевронные колеса изготовляют двух типов (рис. 14): с дорожкой посредине колеса (а) и без дорожки (б). В шевронном колесе осевые силы F_a на полушевронах, направленные в противоположные стороны, взаимно уравновешиваются внутри колеса и на валы и опоры валов не передаются. Поэтому у шевронных колес угол наклона зубьев принимают в пределах  = 25...40°, в результате чего повышается прочность зубьев, плавность работы передачи и ее нагрузочная способность. Шевронные колеса применяют в мощных быстроходных закрытых передачах. Недостатком шевронных колес является высокая трудоемкость и себестоимость изготовления.

Геометрические, кинематические и прочностные расчеты шевронной и косозубой передач аналогичны.

а

б

Рис. 14