1. Постановка проблемы

Различные экономические субъекты имеют разное отношение к риску. Оно принимает широкий спектр значений: от высокой чувствительности к риску до нейтральности к риску и до склонности к риску.

Отношение к риску зависит от субъективных характеристик ЛПР, от имущественного и социального положения ЛПР, от того, чем рискует ЛПР. Очевидно, что чем большее значение принимает случайная величина, отражающая доход, тем чувствительнее ЛПР к риску.

Надо математическими методами оценить отношение ЛПР к риску и затем применять полученные оценки в моделях принятия решения.

Существует набор таких методов.

Первый метод – это интегральный взвешенный критерий. Недостаток его в том, что λ – оценочное значение и следовательно не имеет достаточного основания для использования.

Другие методы: измерение отношения к риску с помощью предельной полезности денежного дохода, измерение отношения к риску с помощью безусловного денежного эквивалента.

2. Связь отношения к риску и функции полезности денежного дохода

Пусть ситуация выбора содержит две альтернативы:

1. принять рискованное решение с возможным доходом или проигрышем

2. отказаться от этого решения

Если субъект безразличен к риску, то он найдет величину ожидаемого дохода при рискованном решении и если она больше нуля, примет первую альтернативу, а если меньше нуля – вторую.

Чтобы учесть различные варианты отношения людей к риску введем функцию полезности денежного дохода:

U=u(x)

Это некоторая функция полезности монотонно возрастающая по x:

Если для ЛПР определена функция полезности денежного дохода, то он для различных альтернатив находит их ожидаемые значения функции полезности и выбирает альтернативу, у которой ожидаемое значение полезности будет наибольшим.

Предположим, что задана функция полезности денежного дохода:

U=u(x)

Обозначим: x₀ – начальное значение дохода,

x₁=x₀+Δx (Δx>0) – доход в случае успешной реализации рискованного решения

x₂=x₀–Δx (Δx>0) – доход в случае неудачной реализации рискованного решения

Покажем, что выбор альтернативы зависит от вида функции полезности.

Рассмотрим три случая задания функции полезности.

Первый случай.

Функция полезности линейная

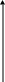u

u(x)

u ₁

u ₀

u ₂

x

x₂ x₀ x₁

u₀ – полезность в случае отказа от рискованного решения

u₁– полезность в случае успеха

u₁ = u(x₁)

u₂– полезность в случае неудачи

u₂ = u(x₂)

u₁– u₀ = u₀ – u₂

Для ЛПР безразлично, какое решение принимать.

ЛПР безразличен к риску.

Второй случай.

Функция полезности выпуклая

u

u(x)

u ₁

u ₀

u ₂

x₂ x₀ x₁ x

MU убывает по X

u₁– u₀ < u₀ – u₂

ЛПР откажется от рискованного решения.

ЛПР чувствителен к риску

Третий случай

Функция полезности вогнутая

u

u(x)

u ₁

u₀

u ₂

x₂ x₀ x₁ x

MU возрастает по X

u₁– u₀ > u₀ – u₂

ЛПР примет рискованное решение.

ЛПР склонен к риску.

Итак:

• если ЛПР нейтрален (безразличен) к риску, то его функция полезности линейная, а предельная полезность постоянная,

• если ЛПР чувствителен к риску (избегает риска), то его функция дохода выпуклая, а предельная полезность убывает,

• если ЛПР склонен к риску, то его функция денежного дохода вогнутая, а предельная полезность является возрастающей.