Типы поляризации

В зависимости от механизма поляризации, поляризацию диэлектриков можно подразделить на следующие типы:

• Электронная — смещение электронных оболочек атомов под действием внешнего электрического поля. Самая быстрая поляризация (до 10⁻¹⁵ с). Не связана с потерями.

• Ионная — смещение узлов кристаллической структуры под действием внешнего электрического поля, причем смещение на величину, меньшую, чем величинапостоянной решетки. Время протекания 10⁻¹³ с, без потерь.

• Дипольная (Ориентационная) — протекает с потерями на преодоление сил связи и внутреннего трения. Связана с ориентацией диполей во внешнем электрическом поле.

• Электронно-релаксационная — ориентация дефектных электронов во внешнем электрическом поле.

• Ионно-релаксационная — смещение ионов, слабо закрепленных в узлах кристаллической структуры, либо находящихся в междуузлие.

• Структурная — ориентация примесей и неоднородных макроскопических включений в диэлектрике. Самый медленный тип.

• Самопроизвольная (спонтанная) — благодаря этому типу поляризации у диэлектриков, у которых он наблюдается, поляризация проявляет существенно нелинейные свойства даже при малых значениях внешнего поля, наблюдается явление гистерезиса. Такие диэлектрики (сегнетоэлектрики) отличаются очень высокими значениямидиэлектрической проницаемости (от 900 до 7500 у некоторых видов конденсаторной керамики). Введение спонтанной поляризации, как правило, увеличивает тангенс угла потерь материала (до 10⁻²)

• Резонансная — ориентация частиц, собственные частоты которых совпадают с частотами внешнего электрического поля.

• Миграционная поляризация обусловлена наличием в материале слоев с различной проводимостью, образованию объемных зарядов, особенно при высоких градиентах напряжения, имеет большие потери и является поляризацией замедленного действия.

Поляризация диэлектриков (за исключением резонансной) максимальна в статических электрических полях. В переменных полях, в связи с наличием инерции электронов, ионов и электрических диполей, вектор электрической поляризации зависит от частоты.

Электри́ческий ди́польный моме́нт — векторная физическая величина, характеризующая, наряду с суммарным зарядом (и реже используемыми высшими мультипольными моментами), электрические свойства системы заряженных частиц (распределениязарядов) в смысле создаваемого ею поля и действия на нее внешних полей. Главная после суммарного заряда и положения системы в целом (ее радиус-вектора) характеристика конфигурации зарядов системы при наблюдении ее издали.

Простейшая система зарядов, имеющая определенный (не зависящий от выбора начала координат) ненулевой дипольный момент — это диполь (две точечные частицы с одинаковыми по величине разноимёнными зарядами). Электрический дипольный момент такой системы по модулю равен произведению величины положительного заряда на расстояние между зарядами и направлен от отрицательного заряда к положительному, или:

где q — величина положительного заряда,   — вектор с началом в отрицательном заряде и концом в положительном.

Для системы из N частиц электрический дипольный момент равен

где   — заряд частицы с номером   а   — её радиус-вектор; или, если суммировать отдельно по положительным и отрицательным зарядам:

Диполь   электрический, совокупность двух равных по абсолютной величине разноимённых точечных зарядов, находящихся на некотором расстоянии друг от друга. Основной характеристикой электрического Д. является его дипольный момент — вектор, направленный от отрицательного заряда к положительному (рис. 1) и численно равный произведению заряда е на расстояние lмежду зарядами: р = el. Дипольный момент определяет электрическое поле Д. на большом расстоянии R от Д. (R»l), а также воздействие на Д. внешнего электрического поля.

Вдали от Д. его электрическое поле Е убывает с расстоянием как 1/R³, т. е. быстрее, чем поле точечного заряда (Диполь 1/R²). Компоненты напряжённости поля Е вдоль оси Д. (E_p) и в направлении, перпендикулярном к р (E_┴), пропорциональны дипольному моменту и в системе единиц СГС (Гаусса) равны:

         

где ϑ — угол между р и радиусом-вектором R точки пространства, в которой измеряется поле Д.; полная напряжённость

         

 Т. о., на оси Д. при ϑ = 0 напряжённость поля вдвое больше, чем при ϑ = 90°; при обоих этих углах оно имеет только компоненту E_p, причём при ϑ = 0 её направление параллельно р, а при ϑ = 90° — антипараллельно (рис. 2)

(рис. 1)

 Рис. 1. Электрический диполь: заряды -е и +е на расстоянии l друг от друга. Дипольный момент диполя р = el полностью определяет электрическое поле диполя на расстояниях R>>I.

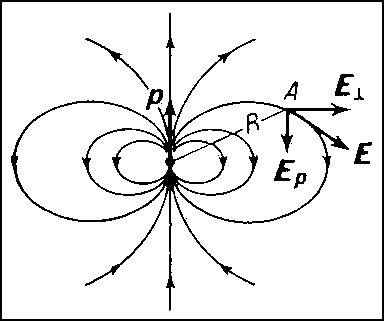рис. 2)

 Рис. 2. Электрическое поле диполя, изображенное с помощью силовых линий. В точке наблюдения А, находящейся на расстоянии R от центра диполя (R>>l), поле Е (направленное по касательной к силовой линии) разложено на 2 компоненты: E_p — параллельную оси диполя и E