5.4.2. Биения

Особый интерес представляет случай, когда два складываемых гармонических колебания мало отличаются по частоте. Результирующее движение при этих условиях можно рассматривать как гармонические колебания с пульсирующей амплитудой. Такие колебания называются биениями.

Обозначим частоту одного из колебаний через , а частоту второго колебания через  + . По условию  << . Амплитуды обоих колебаний будем полагать одинаковыми и равными А. Допустим, что начальные фазы обоих колебаний равны нулю, тогда уравнения колебаний будут иметь следующий вид:

x₁ = A cos  t , x₂ = A cos ( + ) t . (5.34)

Складывая эти выражения и применяя тригонометрическую формулу для суммы косинусов, получим

x = x₁ + x₂ = (2A cos ) cos t (5.35)

(во втором множителе пренебрегаем членом  по сравнению с ). График функции (5.35) представлен на рис. 5.7, а. Изображен случай / = 10.

З

Рис. 5.7.

аключенный в скобки множитель в формуле (5.35) изменяется гораздо медленнее, чем второй множитель. Вследствие условия  >>  за то время, за которое множитель cos t совершает несколько полных колебаний, множитель, стоящий в скобках, почти не изменится. Это дает нам основание рассматривать колебание (5.35) как гармоническое колебание частоты , амплитуда которого изменяется по некоторому периодическому закону. График амплитуды показан на рис. 5.7,б. Аналитическое выражение амплитуды, очевидно, имеет вид

Амплитуда = 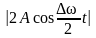. (5.36)

Выражение (5.36) является периодической функцией с частотой, в 2 раза превышающей частоту выражения, стоящего под знаком модуля, т.е. с частотой . Таким образом, частота пульсаций амплитуды – ее называют частотой биения – равна разности частот складываемых колебаний.

20. Векторные диаграммы для представления гармонических колебаний.

Дефференциальное уравнение гармонических колебаний.

Энергия колебательных движений.

Общее решение уравнения (5.3) имеет вид:

x = A cos (ω₀t + α) ,

где А и α – произвольные постоянные.

Таким образом, смещение х изменяется со временем по закону косинуса. Следовательно, движение системы, находящейся под действием силы вида F =  kx, представляет собой гармоническое колебание. Реальные колебания бывают гармоническими, если они малые, любые конечные колебания ангармоничны.

Г рафик гармонического колебания, т.е. график функции (5.4), показан на рис. 5.1. По горизонтальной оси отложено время t, по вертикальной оси – смещение х.

Поскольку косинус изменяется в пределах от –1 до +1, значения х лежат в пределах от –А до +А. Величина наибольшего отклонения системы от положения равновесия называется амплитудой колебания. Амплитуда А  постоянная положительная величина. Ее значение определяется величиной начального отклонения или толчка, которым система была выведена из положения равновесия.

Величина (₀t+), стоящая под знаком косинуса, называется фазой колебания. Она характеризует состояние колеблющейся системы в произвольный момент времени t. Постоянная , характеризующая состояние системы в начальный момент времени t = 0, называется начальной фазой колебания. Поскольку косинус – периодическая функция с периодом 2, различные состояния системы, совершающей гармонические колебания, повторяются через такой промежуток времени Т, за который фаза колебания получает приращение, равное 2 (рис.5.1). Этот промежуток времени называется периодом колебания.,

. (5.5)

Число колебаний, совершающихся в единицу времени, называется частотой колебания . Частота связана с периодом колебания Т следующим образом:

. (5.6)

За единицу частоты принимается частота такого колебания, период которого равен 1 с. Эту единицу называют герцем (Гц). Частота в 10³ Гц называется килогерцем (кГц), в 10⁶ Гц – мегагерцем (МГц).

Из соотношения (5.5) следует, что:

. (5.7)

Таким образом, ₀ дает число колебаний за 2 секунд. Величина ₀ называется циклической (круговой) собственной частотой колеблющейся системы. Она связана с частотой  соотношением

₀ = 2 . (5.8)

Продифференцировав (5.4) по времени, получим выражение для скорости тела, совершающего колебательное движение:

v = A₀ sin (₀t + ) = A₀ cos (₀t +  + ) . (5.9)

Как видно из (5.9), скорость также изменяется по гармоническому закону, причем амплитуда колебаний скорости A₀. Из сравнения (5.4) и (5.9) следует, что скорость с амплитудой А₀ опережает смещение по фазе на .

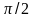Продифференцировав (5.9) по времени еще раз, найдем выражение для ускорения этого тела:

а = A cos (₀ t +) =

=A cos (₀ t +  +) . (5.10)

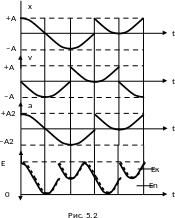
Как следует из (5.10), ускорение и смещение меняются в противофазе. Это означает, что в тот момент, когда смещение достигает положительного наибольшего значения, ускорение достигает наибольшего по модулю отрицательного значения, и наоборот.

На рис. 5.2 сопоставлены графики для смещения, скорости и ускорения.