
- •2.1. Фундаментальные взаимодействия
- •2.5. Второй закон Ньютона
- •2.6. Третий закон Ньютона и закон сохранения импульса
- •9. Вращение твердого тела относительно неподвижной оси. Основной закон динамики вращательного движения абсолютно твердого тела. Момент инерции.
- •5.4.2. Биения
- •20. Векторные диаграммы для представления гармонических колебаний.
- •5.2.2. Динамические характеристики гармонического колебания
- •Потенциальная энергия
- •17. Вязкость. Движение тел в жидкостях и газах.
- •7.16. Движение тел в жидкостях и газах
- •30.Уравнение состояния идеального газа
- •Произведение na равно числу молекул n, содержащихся в массе газа m. С учетом этого получим
- •А с учетом того, что число молекул в единице объема, можно записать:
- •7.3. Газообразное состояние вещества. Идеальный газ
- •Суммарный собственный объем частиц намного меньше размеров сосуда, в котором они находятся;
- •Частицы взаимодействуют друг с другом только во время столкновений;
- •7.Поляризация диэлектриков. Вектор поляризации, электрический диполь. Электрический момент диполя. Полярные и неполярные молекулы.
- •Типы поляризации
- •§ 15. Полярные и неполярные молекулы
- •Для характеристики волн используется волновое число
- •Учитывая (6.8), уравнению (6.7) можно придать вид
- •Колебательный контур
- •Энергия заряженного проводника — Поверхность проводника является эквипотенциальной. Поэтому потенциалы тех точек, в которых находятся точечные заряды , одинаковы и равны потенциалу проводника.
- •Энергия заряженного конденсатора — когда потенциал обкладки конденсатора, на которой находится заряд , равен а потенциал обкладки, на которой находится заряд , равен . Формула выглядит так:
- •Энергия и плотность энергии электростатического поля
Энергия заряженного проводника — Поверхность проводника является эквипотенциальной. Поэтому потенциалы тех точек, в которых находятся точечные заряды , одинаковы и равны потенциалу проводника.
![]()
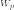 —
Энергия заряженного
проводника
—
Энергия заряженного
проводника![]() —
Потенциал проводника
—
Потенциал проводника
![]() —
Точечный заряд
—
Точечный заряд
Энергия заряженного конденсатора — когда потенциал обкладки конденсатора, на которой находится заряд , равен а потенциал обкладки, на которой находится заряд , равен . Формула выглядит так:
![]()
Или можно преобразовать
![]()
— Энергия заряженного конденсатора
— Потенциал проводника
— Точечный заряд
![]() —
Напряжение
—
Напряжение
Энергия и плотность энергии электростатического поля
Если к пластинам заряженного конденсатора присоединить лампочку, то она вспыхнет, а конденсатор разрядится, и электростатическое поле между его пластинами исчезнет. Следовательно, электростатическое поле конденсатора обладает энергией, которая и превратилась в световую.
Рассчитаем энергию заряженного конденсатора, заряд которого q, напряжение на конденсаторе U, емкость С.
В процессе разрядки конденсатора разность потенциалов между обкладками равномерно убывает от U до нуля, среднее же значение разности потенциалов равно
![]()
Тогда
работа A, совершаемая электрическим
полем при разряде конденсатора,
![]()
а энергия, которой обладает заряженный конденсатор, равна этой работе.Этой энергией обладает электростатическое поле конденсатора. Выразим ее через характеристики поля. Подставив в формулу
![]()
выражение
![]()
а также U = Ed, имеем
![]()
Энергия однородного поля пропорциональна объему, занимаемому полем. В связи с этим говорят об энергии единицы объема поля (объемной плотности энергии — We).
![]()
В СИ единицей объемной плотности энергии является джоуль на кубический метр (Дж/м3).
Тогда
![]()
Полученная формула справедлива не только для однородного электростатического поля, но и для любого другого электростатического поля, а также и для переменного электрического поля.
ферромагнетизм
К ферромагнетикам (ferrum –
железо) относятся вещества, магнитная
восприимчивость которых положительна
и достигает значений ![]() .
Намагниченность
.
Намагниченность ![]() и
магнитная индукция
и
магнитная индукция ![]() ферромагнетиков
растут с увеличением напряженности
магнитного поля
ферромагнетиков
растут с увеличением напряженности
магнитного поля ![]() нелинейно,
и в полях
нелинейно,
и в полях ![]() намагниченность
ферромагнетиков достигает предельного
значения
намагниченность
ферромагнетиков достигает предельного
значения ![]() ,
а вектор магнитной индукции растет
линейно с
:
,
а вектор магнитной индукции растет
линейно с
: ![]()
Ферромагнитные
свойства материалов проявляются только
у веществ в твердом состоянии, атомы
которых обладают постоянным спиновым,
или орбитальным, магнитным моментом, в
частности у атомов с недостроенными
внутренними электронными оболочками.
Типичными ферромагнетиками являются
переходные металлы. В ферромагнетиках
происходит резкое усиление внешних
магнитных полей. Причем для
ферромагнетиков ![]() сложным
образом зависит от величины магнитного
поля. Типичными ферромагнетиками
являются Fe, Co, Ni, Gd, Tb, Dy, Ho, Er, Tm, а
также соединения ферромагнитных
материалов с неферромагнитными:
сложным
образом зависит от величины магнитного
поля. Типичными ферромагнетиками
являются Fe, Co, Ni, Gd, Tb, Dy, Ho, Er, Tm, а
также соединения ферромагнитных
материалов с неферромагнитными: ![]() ,
, ![]() ,
, ![]() и
др.
и
др.
Существенным
отличием ферромагнетиков от диа- и
парамагнетиков является наличие у
ферромагнетиков самопроизвольной
(спонтанной) намагниченности в отсутствие
внешнего магнитного поля. Наличие у
ферромагнетиков самопроизвольного
магнитного момента ![]() в
отсутствие внешнего магнитного поля
означает, что электронные спины и
магнитные моменты атомных носителей
магнетизма ориентированы в веществе
упорядоченным образом.
в
отсутствие внешнего магнитного поля
означает, что электронные спины и
магнитные моменты атомных носителей
магнетизма ориентированы в веществе
упорядоченным образом.
Ферромагнетики – это вещества, обладающие самопроизвольной намагниченностью, которая сильно изменяется под влиянием внешних воздействий – магнитного поля, деформации, температуры.
Ферромагнетики, в отличие от слабо магнитных диа- и парамагнетиков, являются сильно магнитными веществами: внутреннее магнитное поле в них может в сотни раз превосходить внешнее поле.
Основные отличия магнитных свойств ферромагнетиков.
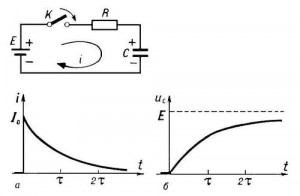
1. Нелинейная зависимость намагниченности от напряженности магнитного поля Н (рис. 6.5).
Как
видно из рис. 6.5, при ![]() наблюдается
магнитное насыщение.
наблюдается
магнитное насыщение.
2.
При ![]() зависимость
магнитной индукции В от Н нелинейная,
а при
–
линейная (рис. 6.6).
зависимость
магнитной индукции В от Н нелинейная,
а при
–
линейная (рис. 6.6).
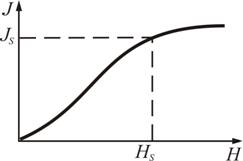
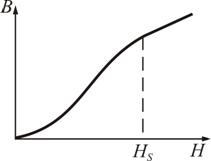
Рис. 6.5 Рис. 6.6
3.
Зависимость относительной магнитной
проницаемости от Н имеет
сложный характер (рис. 6.7), причем
максимальные значения μ очень велики
( ![]() ).
).
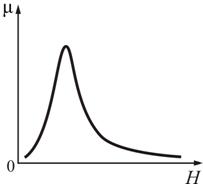
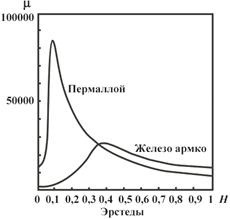
Рис. 6.7 Рис. 6.8
Впервые систематические исследования μ от Н были проведены в 1872 г. А.Г. Столетовым (1839–1896) – выдающимся русским физиком, организатором физической лаборатории в Московском университете. На рис. 6.8. изображена зависимость магнитной проницаемости некоторых ферромагнетиков от напряженности магнитного поля – кривая Столетова.
4.
У каждого ферромагнетика имеется такая
температура, называемая точкой
Кюри ( ![]() ), выше
которой это вещество теряет свои особые
магнитные свойства.
), выше
которой это вещество теряет свои особые
магнитные свойства.
Наличие
температуры Кюри связано с разрушением
при ![]() упорядоченного
состояния в магнитной подсистеме
кристалла – параллельной ориентации
магнитных моментов. Для никеля температура
Кюри равна 360 °С. Если подвесить образец
никеля вблизи пламени горелки так, чтобы
он находился в поле сильного постоянного
магнита, то не нагретый образец может
располагаться горизонтально, сильно
притягиваясь к магниту (рис. 6.9). По мере
нагрева образца и достижения
температуры
ферромагнитные
свойства у никеля исчезают и образец
никеля падает. Остыв до температуры
ниже точки Кюри, образец вновь притянется
к магниту. Нагревшись, вновь падает и
т.д., колебания будут продолжаться все
время, пока горит свеча.
упорядоченного
состояния в магнитной подсистеме
кристалла – параллельной ориентации
магнитных моментов. Для никеля температура
Кюри равна 360 °С. Если подвесить образец
никеля вблизи пламени горелки так, чтобы
он находился в поле сильного постоянного
магнита, то не нагретый образец может
располагаться горизонтально, сильно
притягиваясь к магниту (рис. 6.9). По мере
нагрева образца и достижения
температуры
ферромагнитные
свойства у никеля исчезают и образец
никеля падает. Остыв до температуры
ниже точки Кюри, образец вновь притянется
к магниту. Нагревшись, вновь падает и
т.д., колебания будут продолжаться все
время, пока горит свеча.
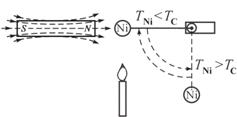
Рис. 6.9
5. Существование магнитного гистерезиса.
На рисунке 6.10 показана петля гистерезиса – график зависимости намагниченности вещества от напряженности магнитного поля Н.
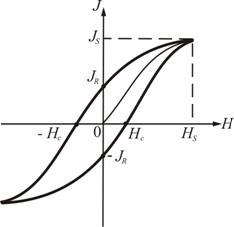
Рис. 6.10
Намагниченность ![]() при
при ![]() называется намагниченностью
насыщения.
Намагниченность
называется намагниченностью
насыщения.
Намагниченность ![]() при
при ![]() называется остаточной
намагниченностью (что
необходимо для создания постоянных
магнитов). Напряженность
называется остаточной
намагниченностью (что
необходимо для создания постоянных
магнитов). Напряженность ![]() магнитного
поля, полностью размагниченного
ферромагнетика, называется коэрцитивной
силой.
Она характеризует способность
ферромагнетика сохранять намагниченное
состояние.
магнитного
поля, полностью размагниченного
ферромагнетика, называется коэрцитивной
силой.
Она характеризует способность
ферромагнетика сохранять намагниченное
состояние.
Большой коэрцитивной силой (широкой петлей гистерезиса) обладают магнитотвердые материалы. Малую коэрцитивную силу имеют магнитомягкие материалы.
Измерение гиромагнитного отношения для ферромагнетиков показали, что элементарными носителями магнетизма в них являются спиновые магнитные моменты электронов.
Ферромагнитные материалы играют огромную роль в самых различных областях современной техники. Магнитомягкие материалы используются в электротехнике при изготовлении трансформаторов, электромоторов, генераторов, в слаботочной технике связи и радиотехнике; магнитожесткие материалы применяют при изготовлении постоянных магнитов.
Широкое
распространение в радиотехнике, особенно
в высокочастотной радиотехнике, получили
ферриты ( ![]() )
сочетающие ферромагнитные и
полупроводниковые свойства.
)
сочетающие ферромагнитные и
полупроводниковые свойства.
Ферритами называют ферромагнитные материалы, получаемые из смеси окислов железа, цинка и других элементов. При изготовлении магнитопроводов смесь размалывают, прессуют и отжигают при температуре около 1200 0С; таким образом, получают магнитопроводы нужной формы. Ферриты обладают очень большим удельным сопротивлением, вследствие чего потери из-за вихревых токов чрезвычайно, малы и их можно применять при высокой частоте.
Ферриты обладают значительной начальной магнитной проницаемостью, незначительной индукцией насыщения(0,18 – 0,32Тл) и малой коэрцитивной силой (8 – 80 А/м).
