§13. Энтропия, ее связь с термодинамической вероятностью.

Опр. Отношение теплоты Q, полученной телом в изотермическом процессе, к температуре Т теплоотдающего тела наз. приведенным количеством теплоты.

Приведенное количество теплоты (ПКТ), сообщаемое телу на бесконечно малом участке процесса, есть Q/T.

Можно показать, что ПКТ, сообщаемое телу в любом обратимом круговом процессе, равно нулю: (13.1).

Из равенства нулю интеграла, взятого по замкнутому контуру, следует, что подинтегральное выражение Q/T есть полный дифференциал некоторой функции состояния. Обозначаем : Q/T=dS (13.2).

Опр. Функция состояния, дифференциалом которой является Q/T, наз. энтропией и обозначается S.

Из (13.1) следует, что для обратимых процессов изменение энтропии . В термодинамике доказывается, что энтропия системы, совершающей необратимый цикл, возрастает: . Это относится лишь к замкнутым системам; если же система обменивается теплотой с внешней средой, то ее энтропия может вести себя любым образом.

Итак, для замкнутой системы выполняется закон неубывания энтропии: - неравенство Клаузиуса.

Если система совершает равновесный переход из состояния 1 в 2, то изменение энтропии: , где подинтегральное выражение можно выразить через параметры состояния. Таким способом мы получим энтропию с точностью до аддитивной постоянной. Физический смысл имеет не само значение энтропии, а разность энтропий.

Энтропия в изопроцессах.

, . Тогда 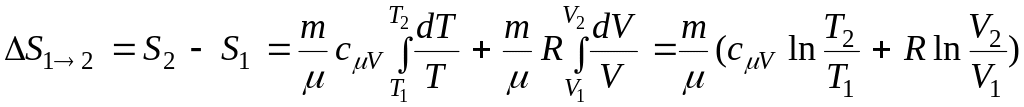т.е. изменение энтропии идеального газа при переходе его из одного состояния в другое не зависит от вида процесса перехода 12.

1. Т.к. для адиабатического процесса Q=0, то S=0, S=const, т.е. адиабатный процесс протекает при постоянной энтропии (это – изоэнтропийный процесс).

2. При изотермическом процессе Т₁=Т₂: . (13.3)

3. При изохорном процессе V₁=V₂: 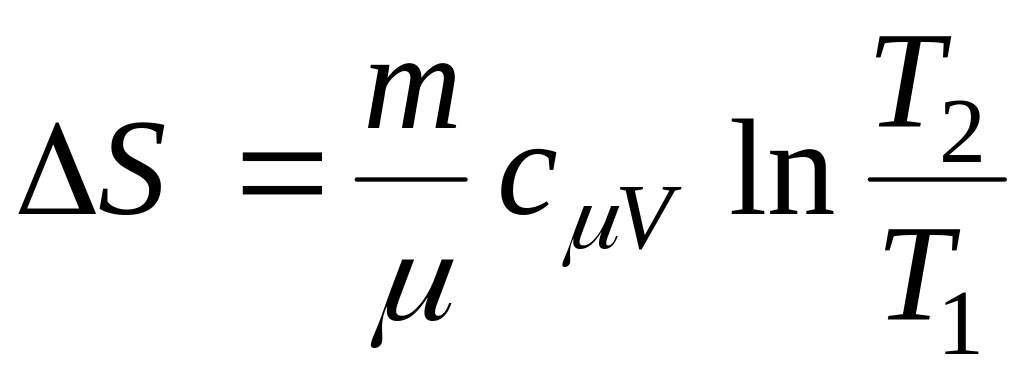. (13.4)

4. При изобарном: . (13.5)

Энтропия обладает свойством аддитивности: энтропия системы равна сумме энтропий тел, входящих в нее. ВЭ также аддитивна.

Опр. Термодинамической вероятностью W состояния системы наз. число способов, которыми может быть реализовано данное состояние макроскопической системы, или число микросостояний, осуществляющих данное макросостояние (по определению W>1).

Согласно Больцману (1872), энтропия S системы пропорциональна W:

S=k ln W (13.6),

Где k – постоянная Больцмана.

Т.о., энтропия определяется логарифмом числа микросостояний, с помощью которых может быть реализовано данное макросостояние. Следовательно, энтропия может рассматриваться как мера вероятности состояния ТС. (13.6) позволяет дать энтропии следующее статистическое толкование: энтропия является мерой неупорядоченности системы. Дей-но, чем больше число микросостояний, реализующих данное макросостояние, тем больше энтропия. В состоянии равновесия – наиболее вероятного состояния системы – число микросостояний максимально, при этом максимальна и энтропия.

Т.к. реальные процессы необратимы, то можно утверждать, что все процессы в замкнутой системе ведут к увеличению ее энтропии – принцип возрастания энтропии. При статистическом толковании энтропии это означает, что прицессы в замкнутой системе идут в направлении от менее вероятных к более вероятным, до тех пор пока вероятность состояния не станет максимальной. Это может нарушаться в системах с малым числом частиц: могут наблюдаться флуктуации.