§6. Закон Максвелла для распределения молекул идеального газа по скоростям и энергиям теплового движения.

Средняя квадратичная скорость молекул в газе в состоянии равновесия при Т=const остается постоянной: (10). Это объясняется тем, что в газе при этом устанавливается некоторое стационарное (не меняющееся со временем) распределение молекул по скоростям, которое подчиняется вполне определенному статистическому закону. Этот закон теоретически выведен Дж. Максвеллом.

При выводе этого закона распределения Максвелл предполагал, что газ состоит из очень большого числа N тождественных молекул, находящихся в состоянии беспорядочного теплового движения при одинаковой температуре. Предполагалось также, что силовые поля на газ не действуют.

Закон Максвелла описывается функцией f(v) распределения молекул по скоростям. Если разбить диапазон скоростей молекул на малые интервалы, равные dv, то на каждый интервал скорости будет приходиться некоторое число молекул dN(v), имеющих скорость, заключенную в этом интервале.

Функция f(v) определяет относительное число молекул dN(v)/N, скорости которых лежат в интервале от v до v+d v, т.е. dN(v)/N = f(v)d v, откуда

.

Применяя методы теории вероятностей, Максвелл нашел функцию f(v) – закон для распределения молекул идеального газа по скоростям:

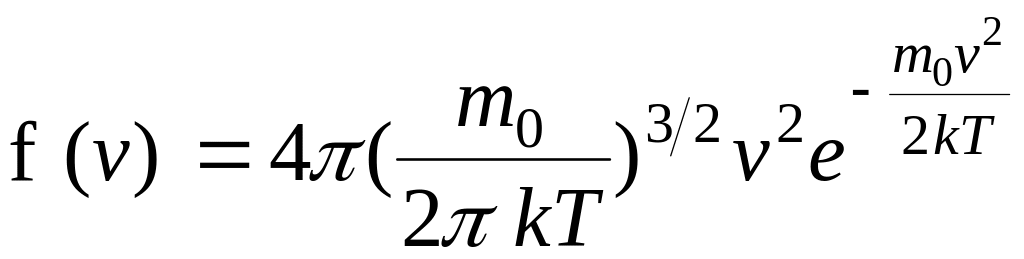(14)

конкретный вид формулы зависит от рода газа (массы молекулы) и от параметра его состояния (температуры).

На графике функция f(v), начинаясь от нуля, достигает максимума при v_в и затем асимптотически стремится к нулю. Кривая не симметрична относительно v_в.

Относительное число молекул в интервале от v до v+d v находится как площадь полоски под графиком.

Площадь, ограниченная кривой распределения и осью абсцисс, равна единице. Это означает, что функция f(v) удовлетворяет условияю нармировки:

.

Скорость, при которой функция распределения максимальна, наз. наиболее вероятной скоростью. Методоами дифференциального исчисления можно найти: (15). Отсюда: при повышении температуры максимум функции распределения сместится вправо (значение наиболее вероятной скорости становится больше); а площадь остается неизменной, поэтому при повышении температуры кривая распределения бедет растягиваться и понижаться.

Средняя скорость молекулы (средняя арифметическая скорость) определяется по формуле: , откуда: (16).

Скорости, характеризующие состояние газа:

1. наиболее вероятная (вероятнейшая) ;

2. средняя ;

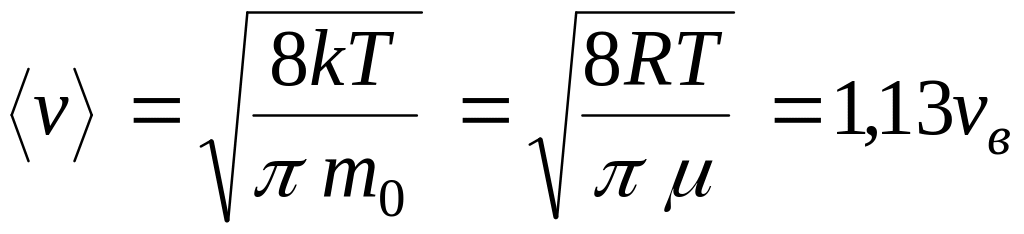3. средняя квадратичная 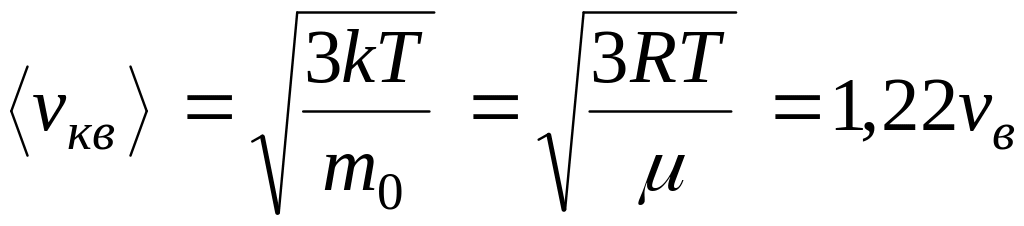. (рис.)

Исходя из распределения молекул по скоростям 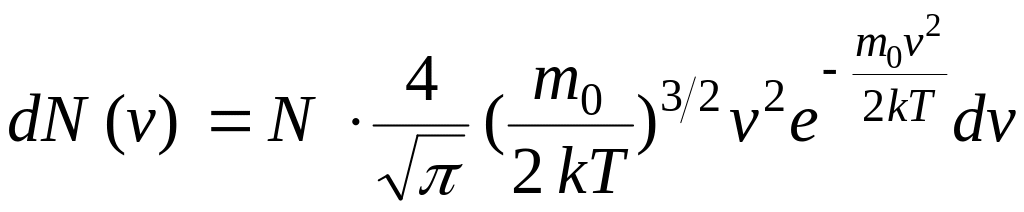(17) можно найти распределение молекул газа по значениям кинетической энергии . Для этого перейдем от переменной v к переменной . Подставив в (17) и , получим , где - число молекул, имеющих кинетическую энергию поступательного движения, заключенную в интервале от до .

Т.о., функция распределения молекул по энергиям теплового движения . Тогда средняя кинетическая энергия молекулы идеального газа .

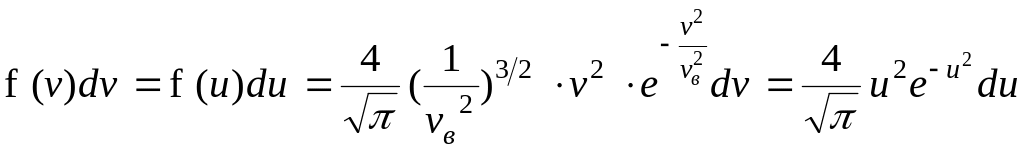Для решения конкретных задач чаще употребляется универсальное распределение Максвелла, которое совершенно одинаково выглядит для любого газа и при любой температуре. В качестве переменной берется отношение , тогда . Подставим в (14): откуда - одинакова для всех газов.

Существуют таблицы значений универсальной функции распределения Максвелла для разных значений u.

П.1. Опыты Штерна и Ламмерта.

Опыт Штерна. Первое экспериментальное определение скоростей молекул выполнено немецким физиком О.Штерном (1888-1970). Его опыты позволили также оценить распределение молекул по скоростям. Схема установки: два коаксиальных цилиндра, по оси внутреннего цилиндра с щелью натянута платиновая проволока, покрытая слоем серебра, которая нагревается током при откачанном воздухе. При нагревании серебро испаряется. Атомы серебра, вылетая через щель, попадают на внутренную поверхность второго цилиндра, давая изображение щели О.

Если прибор привести во вращательное движение вокруг общей оси цилиндров (45 об/с), то атомы серебра осядут не против щели, а сместятся от точки О на некоторое расстояние s. Изображение щели получается размытым. Исследуя толщину осажденного слоя, можно оценить распределение молекул по скоростям, к-е соответствует максвеловскому распределению.

Зная радиусы цилиндров, их угловую скорость вращения, а также измеряя s, можно вычислить скорость движения атомов серебра при данной температуре проволоки. Результаты опытов показали, что средняя скорость атомов серебра близка к той, к-я следует из максвеловского распределения молекул по скоростям.

Опыт Ламмерта. Этот опыт позволяет более точно определить закон распределения молекул по скоростям. Схема установки на рис. Молекулярный пучек от источника проходит через щель и попадает в приемник. Между источником и приемником помещают два диска с прорезями, закрепленных на общей оси. При неподвижных дисках молекулы достигают приемника, проходя через прорези в обоих дисках. Если ось привести во вращение, то приемника достигнут только те прошедшие прорезь в первом диске молекулы, которые затрачивают для пробега между дисками время, равное или кратное времени оборота диска. Другие же молекулы задерживаются вторым диском. Меняя угловую скорость вращения дисков и измеряя число молекул, попадающих в приемник, можно выявить закон распределения скорсотей молекул. Этот опыт также подтвердил справедливость закона Максвелла.