Раздел III Элементы кинетики

§16. Явления переноса.

В термодинамически неравновесных системах возникают особые необратимые процессы – явления переноса. В результате которых происходит пространственный перенос энергии, массы или импульса. К явлениям переноса относятся теплопроводность (перенос энергии), диффузия (перенос массы) и внутреннее трение (перенос импульса).

Диффузия газов.

Пусть в газе присутствует примесь, концентрация которой изменяется с координатой х (одномерный случай), т.е. различна в разных точках объема. (рис.)

В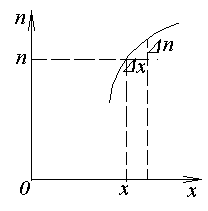 точке с координатой х концентрация n, а в точке сдвинутой на х – n+n. Отношение характеризует быстроту изменения концентрации в пространстве и называется градиентом концентрации. Направление градиента в пространстве (знак «+» или «-» отношения) указывает направление возрастания концентрации. Если градиент концентрации равен нулю, то n везде одинакова. Такое равномерное распределение примеси является наиболее вероятным и, однажды возниконув, не будет нарушаться хаотическим движением молекул.

При наличии градиента концентрации хаотическое движение будет способствовать ее выравниванию, т.е. возникает поток молекул примеси, направленный от мест с меньшей к местам с большей концентрацией. Этот диффузионный поток тем больше, чем выше градиент конц-ции.

Для вычисления диффузионного потока расположим в плоскости х=const контрольную площадку S перпендикулярно к оси х и подсчитаем число молекул примеси, проходящих за время t через эту площадку слева направо и справа налево (рис.)

, где - концентрация примеси слева от площадки.

Т.к. концентрация меняется от точки к точке, то для расчета примем, что все молекулы, проходящие через контрольную площадку, испытали последнее столкновение на одном и том же расстоянии от площадки, равном средней длине свободного пробега l. На пути l столкновений нет и концентрация пучка постоянна и равна ее значению в плоскости х-l.

Аналогично, . Суммарный диффузионный поток через площадку в положительном направлении оси х равен разности этих двух потоков: . Поток через единицу площади за единицу времени: - закон Фика. D – коэффициент диффузии, равный плотности потока молекул примеси при единичном градиенте концентрации.

Коэффициент диффузии (16.1) - получен из МКТ и связан с основными микроскопическими характеристиками. Закон Фика был открыт на опыте задолго до МКТ.

Вязкость газа.

Пусть в покоящемся газе движется вверх перпендикулярно оси х пластинка со скоростью . Пластинка увлекает за собой прилегающий слой газа, который в свою очередь увлекает за собой следующий слой и т.д. Т.о., весь газ как бы делится на тончайшие слои, скользящие вверх тем медленнее, чем дальше они находятся от движущегося тела.

Очевидно, что при отсутствии взаимодействия между слоями газа и между газом и пластинкой, каждый слой мог бы двигаться с произвольной скоростью, независимо от других. В действительности же распределение скоростей v(x) слоев газа от их расстояния до пластинки устанавливается в силу наличия вязкости, т.е. сил внутреннего трения в газе.

Каждая молекула газа принимает участие в 2 движениях: хаотичном (тепловом) и направленном (коллективном). Вектор средней скорости равен нулю в силу хаотичности его направления у отдельных молекул, т.е. совокупность непрерывно сталкивающихся молекул, участвующих только в тепловом движении, в среднем будет оставаться на месте. При наличии же дополнительного направленного движения вся совокупность молекул в целом будет дрейфовать с постоянной скоростью v.

Т.о. средний импульс отдельной молекулы в данном слое . Переходя из слоя в слой молекулы переносят добавочное количество направленного движения, которое передается новому слою. Перемешивание молекул разных слоев (из-за хаотичности теплового движения) приводит к выравниванию скоростей переносного движения v разных слоев, что и проявляется макросткопически как действие сил трения между слоями.

Для вывода количественных закономерностей поступаем аналогично диффузии.

Имеем: , .

Поскольку давление и температура во всем газе одинаковы, то n и одинаковы по всему объему и . Но одинаковые потоки частиц переносят разный импульс: и , где и - скорости направленного движения газа соотсетственно в плоскостях х-l и x+l. Разность и - представляет собой изменени импульса слоя и равна импульсу силы трения, действующей в течение этого времени в направлении v, параллельном площадке S.

Т.е. , а сила трения, действующая на единицу площади границы соприкосновения соседних слоев: - закон Ньютона.

Взаимодействие двух слоев можно рассматривать по закону Ньютона как процесс, при котором от одного слоя к другому передается в единицу времени импульс, по модулю равный действующей силе. Тогда можно записать: (16.2), где - плотность потока импульса – импульс, переносимый в ед. времени через ед. площадку (-ю оси х) в положительном направлении оси х.

- динамическая вязкость (коэффициент внутреннего трения) – вычисляется по формуле: (16.3).

Закон (16.4) определяет и силу трения, возникающую на границе между газом и движущемся в этом газе твердым телом. Можно показать, что сила сопротивления, испытываемая шаром, движущемся в вязком газе, прямопропорциональна вязкости газа , радиусу шара r и скорости его движения : - закон Стокса. Эта формула применима в случае тел достаточно малых размеров и малых скоростей их движения. При больших скоростях вокруг движущихся тел возникают сложные вихревые движения газа, и сила сопротивления возрастает пропорционально квадрату скорости .

Теплопроводность газа.

Рассмотрим газ, заключенный между двумя параллельными стенками разной температуры Т_а и Т_в. проведем ось х перпендикулярно стенкам. Температура промежуточных слоев газа Т(х) будет функцией координаты х.

При наличии градиента температур ( ) через газ в направлении оси х будет идти поток тепла. Механизм переноса тепла состоит в следующем: молекулы в разных слоях имеют разную ср. КЭ из-за различия температур; в силу хаотичности движения молекулы привносят в новый слой энергию покидаемого слоя. Т.о. движение молекул приводит к перемешиванию молекул с разными КЭ, т.е., с макроскопической точки зрения, к потоку тепла.

Аналогично предыдущему, через площадку S переносится тепло , откуда - закон Фурье. - плотность теплового потока, - коэффициент теплопроводности (или просто теплопроводность) газа. Знак «-» указывает, что поток тепла направлен в сторону уменьшения температуры.

Средняя энергия всех n молекул в единице объема равна . Если газ нагреть на 1 градус так, чтобы его концентрация осталась прежней (т.е. при неизменном оюъеме), то эта энергия увеличится до . Возрастание энергии при таком процессе: . Получаем (16.4).

Из формул (16.1), (16.4) и (16.3) вытекают простые зависимости между коэффициентами : .

Коэффициент диффузии при обычных давлениях обратно пропорционален давлению: с ростом давления уменьшается длина свободного пробега молекул и затрудняется их диффузия.

Вязкость газа не зависит от давления: с увеличением давления и плотности газа повышается число молекул, переносящих импульс, но уменьшается расстояние, на которое он переносится до столкновений с соседними молекулами. Это вывод получен и экспериментально проверен Максвеллом: даже при тысячекратном изменении давления вязкость почти не меняется.

Т.к. - величина постоянная, то тплопроводность зависит от давления также как и вязкость.