14. Потери напора (давления) в местных сопротивлениях. Коэффициент местного сопротивления.

При определении потери напора необходимо учитывать и местные сопротивления (в сужениях, на расширениях, закруги, в кранах, вентилях и т.д.) Потери напора в местных сопротивлениях, как потери напора для трения выражаются через скоростной напор. Отношение потери напора в данном местном сопротивлении и скорости напору называют коэффициентом местного сопротивления.

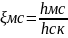Для местного сопротивления можно написать следующие уравнения:

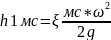
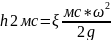
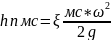
Сложим, левые и правые части этих уравнений.

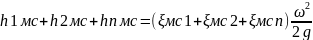
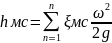
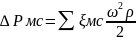
Hп=hтр+hмс-потеря напора

-коэффициент широховатости

l-величина выступа

dэ- эквивалентный диаметр

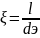или

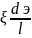
15. Моделирование хтп. Два основных метода моделирования.

Технологические процессы представляют собой сочетание различных физических, физико химических явлений. Пользуясь самыми общими законами физических и химических явлений их описывают дифференциальным уравнением, однако диф. Уравнения отвечают целому классу подобных явлений и для выделения дного конкретного, необходимо ограничить диф. Уравнение доп. Условиями называемыми условиями однозначности.

Метод моделирования-метод исследования ХТП на моделях отличающихся от объекта моделирования (натурой в соновном масштабом) моделирование можно осуществить двумя основными методами:

1)Метод обобщённых переменных

2) Метод числовых экспериментов

16. Сущность моделирования методом обобщенных переменных (физическим моделированием). Виды подобия. Условия однозначности.

Метод обобщённых переменных – составляет основу теории подобия одим из основных принципов теории подобия является выделение из класса явлений группы подобных явлений. Подобные-это такие явления для которых отношение сходств и характеристик их величин постоянны. Различают: 1) геометрические подобия 2) временные подобия 3) Подобия физических величин 4) подобия начальных и граничных условий.

Условия однозначности:

1. Геометрическую форму и размер аппарата

2. Физические свойства веществ учавствующих в процессе

3. Начальное условие (начальная температура, скорость)

4. Граничные условия т.е. условия на входе и на выходе из аппарата

Геометрическое подобие предполагает что сходства и размеры данного тела и ему подобного параллельны и их отношение вражается величиной al-константа подобия.

При временном подобии сходств той части геом. Подобно системе двиг. По геометрическому подобию траектории проходят геометрически подобные пути в промежутке времени отношение которых является постоянной величиной.at

Физическое подобие предполагает что физически в рассматриваемых подобных системах отношение физических констант двух любых сходст. Точек или частиц размещено подобно в пространстве и времени есть величина постоянная.au

Начальные и граничные условия предполагают что начальные состояния и состояния на границах систем подобны. Подобия этих условий соблюдается лишь в тех случаях когда для начальных и граничных условий вделяется геометрическое временное и физическое подобие.

17. Инварианты подобия. Критерии подобия. Индикатор подобия. Обобщенное критериальному уравнение. Определяющие и определяемые критерии подобия.

Если все сходственные величины определяют состояние данной системы измеряют в относительных еденицах то есть брать отношение сходственных величин в переделах каждй системы то отношение этих величин будет так же величиной постоянной и безразмерной.

Геометрическое подобие: L1/L2=l1/l2=…=iL=const

Временное подобие: T1/T2=t1/t2=…=iT=const

Физические величины: U1/U2=u1/u2=…=iU=const

Инварианты подобия отношение двух однородных величин в теории подобия называют симплексами.

Инварианты подобия выраженные отношениями разных величин выражют отношение разнородных величин называются критериями подобия.

Индикатор подобия – С. Указывает на равенство критериев подобия.

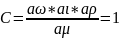
Следовательно, у подобных явлений индикатор подобия=1.

Если константы подобия найдены из условий однозначности то образованные из них критерии называют определяющими.

Критерий в который входит неизвестная величина не входящая в условия однозначности называют определяемой.

f(K1,K2,…,Kn)=0

эту зависимость называют обощённым критериальным уравнением, а критерием подобия K, называют обобщенными переменными величинами. К1=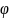 (К2,К3,…,Кn)

К1-определяемый

К2-определяющий