12. Дифференциальное уравнение движения реальной жидкости (уравнение Новье-Стокса).

При движении реальной жидкости в потоке жидкости кроме сил давления и тяжести действуют так же силы трения. Действие сил трения (Т) на выделение в потоке вязкой жидкости элементов параллелепипедов появляется в возникновении на его поверхности касательного напряжения. Касательное напряжение 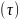определяется как отношение силы трения (Т) к поверхности сопротивления слоёв.

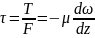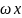где «-» указывает на то что касательное напряжение тормозит слой движения с большей скоростью. Возьмём случай одноименного плоского потока капельной жидкости в направлении оси x в этом случае проекция скорости зависит от расстояния z до горизонтальной плоскости отсчёта. РИС

В этих условиях касательное напряжение возникает в нижней и верхней.

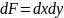
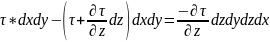Подставим в это выражение значение касательного напряжения по уравнению:

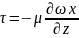
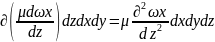
В более общем случае т.е. 3d потока состояние скорости зависит от направлений x,y,z.

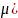
Сумма вторых производных по осям координат

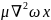
На ось y проекция касательного направления имеет вид:

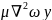
На ось z

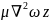
Проекции на оси координат равнодействующих всех сил (тяжести, давления и трения) действуют на элементарный объем капельной жидкости с учтом проекции остаточных сил полученных при выводе уравнений Эйлера сост:

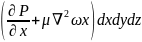
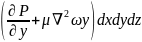
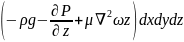
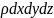
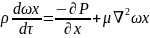
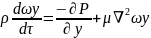
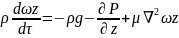
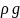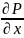
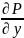
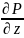Данные уравлнения являются уравнениями Новье-Стокса описывают движение реальных жидкостей. Левые части выражения произведения массы в еденице объема на проекции её ускорения т.е. представляют собой проекции равнодействующих сил энерции возникающие в движении жидкости в правых частях тех же уравнений произведений отражает влияние сил течения. Частные производные отражает влияние изменения гидростатического давления а произведение вязкости на сумму вторичного произведения проекции скорости отражает влияние сил трения на движение жидкости.

13. Уравнение потери напора (давления) на трение о стенки трубопровода (уравнение Дарси Вейбаха). Коэффициент сопротивления трения, коэффициент трения (Дарси).

При гидродинамическом напоре Н и отсутствии сопростивления (hп=0) скорость дивжения жидкости по трубопроводу будет равна скорости истечения жидкости из трубопровода

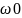
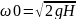
В реальных трубопроводах часть общего напора расходуется на преодоление сопротивления и действительная скорость будет намного меньше скорости

При фактической скорости движения скоростной напок т.е. напор в котором обусловлена эта скорость. Выражается уравнением

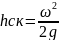
Напор потери на трение hтр можно представить в долях от скоростного напора

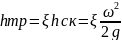
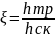
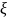- коэффициент сопротивления трения (кси) эта величина показывает во сколько раз напор потери на трение отличается от скоростного напора . На основании закона Н. (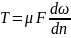 ) сила внешнего трения движения жидкости зависит от вязкости жидкости и скорости движения. т.е. является функцией критерия Рейнольдса. Очевидно так же, что сопротивление трения жидкости будет тем больше, чем длинее трубопровод и чем меньше его диаметр. Следовательно, в общем виде коэффициент сопротивления трения движения жидкости мб выражен:

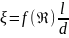
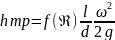
f(Re)= -коэффициент трения(Дарси)

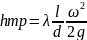Потеря давления на трение или потеря напора на трение

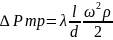Уравнение Дарси – Вейбаха