8. Вязкость. Закон Ньютона.

Движение жидкости значительно зависит от ее вязкости, т.е. от внутреннего трения, которое проявляется при наличии относительного движения соседних слоев жидкости и зависит от сил сцепления между отдельными молекулами.

По закону Ньютона сила внутреннего трения, т.е. сила проявляющая при перемешивании одного слоя жидкости относительно другого прямо пропорционально относстельно скорости перемещения и величине поверхности соприкосновения этих слоев. Она зависит от свойств жидкости и не зависит от давления.

T – сила внутреннего трения

F – площадь поверхности соприкосновения слоев жидкости

- скорость движения жидкости

- малое расстояние между соседними слоями жидкости

- это вязкость такой жидкости, в которой сила в 1Н перемещает находящиеся на расстоянии одного друг друга слои жидкости с поверхностью в 1м² каждый один относительно другого со скоростью 1м/с. Динамический коэффициент вязкости

кинематический коэффициент вязкости.

9. Уравнение неразрывности потока в дифференциальной и интегральной формах.

- составляющая скорости

Данное уравнение называется ДУ неразрывности потока для неустановившегося движения сжимаемой жидкости, которое устанавливает общую зависимость между скоростями в потоке жикости. Данное уравнение показывает изменение массы жидкости в элементарном объеме движущейся жидкости.

Уравнение неразрывности потока в интегральной форме для установившегося движения и называется уравнением постоянства расхода, является частным случаем закона сохранения массы и выражает материальный баланс потока.

10. Дифференциальное уравнение движения идеальной жидкости (уравнение Эйлера).

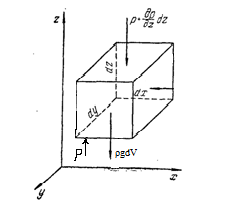
Проекции сил тяжести и сил гидростатического давления

На ось z:

На ось y:

На ось x:

На основании основного принципа динамики: сумма проекций всех сил, действующих на элементарный объем жидкости равна произведению массы жидкости на ускорение.

Разложим ускорение по соответствующим осям координат

ДУ движения Эйлера

11. Уравнение Бернулли.

Берём дифференциальные уравнения Эйлера

Умножим левые и правые части уравнений соответственно на dx, dy,dz и разделим обе части на . В результате имеем:

Складываем левые и правые части уравнений:

правую часть переносим в левую и делим на g

При g и =const, значения дифференциальной суммы

Проинтегрируем: (гидродинамический напор)

Данное уравнение является уравнением Бернулли для идеальной жидкости.

Скоростной или динамический напор

статический или пьезометрический напор

.Геометрический напор который представляет собой высоту данной части жидкости относительно произв. Выбранной плоскости сравнения.

Уравнение Б. для идеальных жидкостей вормируется:

Для любого сечения трубопровода при установившемся движении идеальной жидкости сума скоростей статического и геомерического напоров величина постоянная. Уравнение Б. выражает частные случаи закона сохранения энергии. В энергетической форме уравнение Б. для идеальной жидкости формируется:

Для любого сечения трубопровода при установившемся движении сумма кинетической и потенциальной энергии жидкости остаётся постоянной.

При изменении сечения трубопровода и соответственно скорости движения жидкости происходит приращение энергии: при сужении частные потенциальные энергии переходят в кинетические и наоборот при расширении трубопроводов часть кинетической переходит в потенциальную. При чём общее количество энергии остаётся постоянным. Таким образом уравнение Б. является материальной формой закона сохранения энергии для идеальных жидкостей при установившемся её движении.

На практике приходится иметь дело не с идеальными а реальными жидкостями. Такими при которых возникают силы трения. Которые обусловлены вязкостью жидкости характером её движения, трением о стенки трубопровода и т.д. На перодоление возникающих сопротивлений должна расходоваться часть энергии, общее количество энергии по длине трубопровода будет непрерывно уменьшаться за счёт перехода потенциальной энергии в энергию затрачиваемую на трение т.е. потерю энергии.

В этом случае сумма членов уравнения Б. будет величиной постоянной только при учёте потери энергии.

Уравнение Бернулли.

hп- потеря энергии или потеря напора, данное уравнение формируется так: для любого сечения трубопровода в котором движутся реальные жидкости при установившемся движении сумма напоров скоростей статична геометрического и статического есть величина постоянная.

При движении жидкости по горизонтальному трубопроводу будут одни и те же, следовательно величина z исклчение и уравнение имеет вид: