Функції належності
Покажемо варіант подання на прикладі трикутних функцій належності. Однак використовується ряд інших – як монотонних, так і немонотонних.
Рис.18. 3. Фазифікація трикутними функціями належності
Основні операції над функціями належності.
Нехай ми маємо об’єднання А В, функція належності для об’єднання множини
Це варіант реалізації, коли операція об’єднання реалізується, як алгебрагічна сума. Інший варіант реалізації об’єднання – операція max.
Операція перетину множин.
Реалізація у вигляді добутку.
Реалізація у вигляді операції min.
Якщо ми візьмемо граничний варіант істино/хибно, то має перехід до чіткої логіки булевої алгебри, де логічне «і» реалізується як операція «min», а чітке «або», як операція «max», отже є узгодження чіткої і нечіткої логіки.
Дефазифікація
Дефазифікація - операція отримання чіткої змінної на основі нечіткої. Це операція протилежна до фазифікації на основі заданих функцій належності.
На основі чіткої змінної отримаємо функцію належності, враховуючи що нечіткий результат може мати складну форму функції належності, використовуючи ряд різних методів дефазифікації, які дають різний результат. А загалом дефазифікація – одна з основних причин невисокої точності методів нечіткої логіки.
Продукційні нечіткі контролери.
У формулюванні продукційних правил містяться нечіткі вказівки, наприклад х≈10, х – рівне дуже малій величині, але найчастіше використовуються наступні правила, прикладом яких є – якщо х в інтервалі 4-6, то y вибрати в інтервалі з 9-10. На основі таких правил формується база знань виду:
………………………………………………
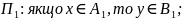
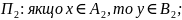
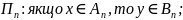
х – ім’я вхідної змінної, у – ім’я вихідної змінної.
Правила такого типу називаються продукційними. Кожне продукційне правило складається з 2-х частин:
- антецедент;
- консецедент.
Приклад: якщо якість виробу добра, то його ціна середня.
Входом в продукційне правило є біжуче значення вхідної змінної, вихідним є нечітка множина. Нечітка множина дефазифікується і в результаті перетворюється у чітку величину.
Операція перетворення вхідної змінної у вихідну носить назву імплікації. Таким чином алгоритм нечіткої логіки здійснює операцію імплікації вхідної змінної у вихідну згідно заданої бази правил. Іноді алгоритми нечіткої логіки називають також контролерами нечіткої логіки.
рис.18. 4. Загальна структура алгоритму (контролера) нечіткої логіки продукційного типу
Блок фазифікації забезпечує перетворення чітких даних у значення відповідних функції належності в діапазоні від 0 до 1. На виході блоку фазифікації ми маємо нечіткі змінні представлені функціями належності.
Блок логічних висновків. Логічні висновки здійснюються для кожного правила окремо, це відповідає антецеденту правила. Наприклад – якщо температура повітря низька і світловий день короткий, то енергоспоживання – велике. Найчастіше в логічному висновку застосовується логічна операція «і» або кон’юнкція над нечіткими множинами. Виконується логічна операція «і» над нечіткими множинами на основі операції мінімум, або операції добуток: min, prod.
Наступний блок є блок під назвою композиція. Кожному правилу відповідає сформована нечітка множина, тому логічні висновки для всіх правил повинні бути об’єднані найчастіше через операцію логічного «або», або диз’юнкцію. Наприклад: якщо температура дуже низька і світлий день – середній, то енергоспоживання велике. Найчастіше операція «або» реалізує застосування операції максимум або сума.
Блок дефазифікації перетворює нечіткий вихід у чіткі числові дані.
Контрольні запитання
Етапи розвитку систем нечіткої логіки.
Вчені, що внесли найбільший вклад в розвиток нечіткої логіки.
Поняття мяких обчислень.
Співвілношення між складністю систем і точністю їх опису.
Типи систем нечіткої логіки. Відмінності між ними.
Спосіб реалізації нечіткого «і».
Спосіб реалізації нечіткого «АБО».
Призначення блоків нечіткої продукційної системи.
Лекція № 20. Приклади розв’язування задач за допомогою засобів ШІ.