Порівняння нейромережних rbf і багатошарових перцептронів

1. RBF мережі забезпечують більшу швидкість навчання і простіше налагодження.

2. RBF мережі дозволяють моделювати поверхні відгуку довільної складності;

3. На відмінну від багатошарових перцептронів мережі RBF не володіють здатністю до екстраполяції даних (якщо точка виходить за межі навчальної вибірки, то результат буде мати низьку точність).

Як спрощений варіант ШНМ RBF розглядають імовірнісні ШНМ і ШНМ узагальненої регресії.

Імовірнісна нейромережа ( PNN – probabilistic neural network) належить до нейромереж з швидким навчанням, але достатньо великими часовими затримками при функціонуванні. Виходи такої мережі можна інтерпретувати, як оцінки ймовірності належності елементу певному класу. Ймовірнісна мережа вчиться оцінювати функцію густини ймовірності, її вихід розглядається як очікуване значення моделі в даній точці простору входів.

При рішенні задач класифікації оцінюється густину ймовірності для кожного класу, порівнюються між собою ймовірності приналежності до різних класів і обирається варіант, для якого густина ймовірності буде найбільшою. Оцінка густини ймовірності в мережі заснована на ядерних оцінках. Якщо приклад розташований в даній точці простору, тоді в цій точці є певна густина ймовірності. Кластери з близько розташованих точок, свідчать, що в цьому місці густина ймовірності велика. Поблизу спостереження є більша довіра до рівня густини, а по мірі віддалення від нього довіра зменшується і плине до нуля. В методі ядерних оцінок в точку, що відповідає кожному прикладу, поміщається деяка проста функція, потім вони всі додаються і в результаті утворюється оцінка для загальної густини ймовірності. Найчастіше в якості ядерних функцій беруть дзвоноподібні функції (гаусові). Якщо є достатня кількість навчальних прикладів, такий метод дає добрі наближення до істинної. Ймовірнісна мережа має три прошарки: вхідний, радіальний та вихідний. Радіальні елементи беруться по одному на кожний приклад. Кожний з них містить гаусову функцію з центром в цьому прикладі. Кожному класу відповідає один вихідний елемент. Вихідний елемент з'єднаний лише з радіальними елементами, що відносяться до його класу і підсумовує виходи всіх елементів, що належать до його класу. Значення вихідних сигналів утворюються пропорційно ядерних оцінок ймовірності приналежності відповідним класам.

Ймовірнісна мережа має три прошарки: вхідний, радіальний та вихідний. Радіальні елементи беруться по одному на кожний приклад. Кожний з них містить гаусову функцію з центром в цьому прикладі. Кожному класу відповідає один вихідний елемент. Вихідний елемент з'єднаний лише з радіальними елементами, що відносяться до його класу і підсумовує виходи всіх елементів, що належать до його класу. Значення вихідних сигналів утворюються пропорційно ядерних оцінок ймовірності приналежності відповідним класам.

1. Маємо тренувальну вибірку з к+m векторів. Нехай к векторів вибірки 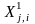, де j=1,…,к – номер вектора, i=1,…,n – номер компоненти вектора представляють перший клас об’єктів, що підлягають класифікації;; всі інші m векторів, що не належать класу 1, відносимо до класу 2. На вхід нейромережі надходить вхідний вектор 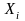, який необхідно класифікувати, тобто встановити імовірність його належності до класу 1.

2. Знаходимо евклідові віддалі вхідного вектора до векторів тренувальної вибірки класів 1 і 2. , .

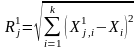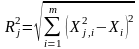3. Переходимо від них до гаусівських віддалей 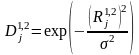, де 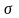- коефіцієнт розмаху функції, що підбирається експериментально.

4. Імовірність належності вхідного вектора до класу 1 обчислюється за формулою 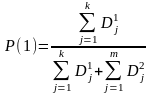. P(1) завжди не перевищує 1, так як сума Р(1)+Р(2) =1.

Нейронна мережа узагальненої регресії (GRNN - General Regression Neural Network) має багато аналогій з імовірнісною нейромережею PNN. Однак основне її призначення – розвязок завдань регресії, зокрема передбачення, прогнозування часових послідовностей.

Подібно до імовірнісної мережа GRNN має три прошарки: вхідний, радіальний та вихідний. Радіальні елементи беруться по одному на кожний приклад. Кожний з них містить гаусову функцію з центром в цьому прикладі. Кожному класу відповідає один вихідний елемент. Вихідний елемент з'єднаний лише з радіальними елементами, що відносяться до його класу і підсумовує виходи всіх елементів, що належать до його класу. Значення вихідних сигналів утворюються пропорційно ядерних оцінок ймовірності приналежності відповідним класам.

1. Маємо тренувальну вибірку з m векторів. Кожен вектор містить набір вхідних (завжди відомих компонентів) 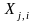, де j=1,…,m – номер вектора, i=1,…,n – номер компоненти вектора та вихідну компоненту 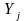, яка відома лише для векторів тренувальної вибірки.

2. Метою нейромережі є передбачення вихідної компоненти 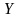для заданого вхідних компонентів вектора .

3. Знаходимо евклідові віддалі вхідного вектора до всіх векторів тренувальної вибірки. .

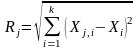4. Переходимо від них до гаусівських віддалей 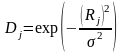, де - коефіцієнт розмаху функції, що підбирається експериментально.

5. Оцінка шуканої вихідної компоненти знаходимо за формулою .

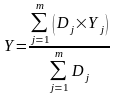Контрольні запитання

1. Топологічні особливості ШНМ RBF.

2. Порівняння БШП і ШНМ RBF.

3. Особливості функцій активації ШНМ RBF.

4. Особливості навчання ШНМ RBF.

5. Недоліки і переваги ШНМ RBF.

6. Особливості і призначення імовірнісних ШНМ.

7. Особливості і призначення ШНМ узагальненої регресії.

Лекція №18. ШНМ геометричних перетворень.

В основі моделювання за допомогою нейроподібних структур геометричних перетворень (ГП) є базовий принцип представлення гіперповерхонь відгуків в ортогональних системах координат ( як прямолінійних, так і криволінійних) моделі, які максимально співпадають з основними вимірами гіперповерхонь. В якості близького аналога нейроподібних структур ГП можна розглянути двошаровий перцептрон автоасоціативного типу, побудований за методом „звуженого горла“ (рис.1). На входи перцептрона подаються одночасно всі компоненти наявних векторів вибірки, ці ж компоненти повторюються як вихідні сигнали тренувальних векторів перцептрона для здійснення навчання. В загальному випадку „звуженого горла“, коли число нейронних елементів прихованого шару менше за число входів (виходів) перетворення вхідних векторів у ідентичні їм вихідні відбувається з певною похибкою. Вихідні сигнали нейронних елементів відображають сигнали головних компонентів. Внаслідок застосування оптимізаційних процедур навчання похибка перетворень вхідних векторів у ідентичні їм вихідні мінімізується, а вихідні сигнали нейронних елементів прихованого шару задають оптимізоване представлення вхідних векторів у новій системі координат зменшеної розмірності. Якщо вхідний вектор автоасоціативної нейромережі включає в себе сигнали вхідних змінних і сигнали відгуків, а число нейронних елементів прихованого шару відповідає розмірності простору еліпсоїда розсіювання, то на виході мережі поверхні відгуків апроксимуються гіперплощинами (площинами), а величини додаткових вимірів представляють похибки такої апроксимації.

Рис.1. НС ГП автоасоціативного типу

Базовим режимом ГП є автоасоціативний режим функціонування. Однак існують суттєві відмінності нейроподібних автоасоціативних структур ГП від багатошарових перцептронів в автоасоціативному варіанті застосування. Основна відмінність полягає в тому, що режим „звуженого горла“ не є обов’язковим для реалізації подібних структур, отже, існує можливість точного (з нульовою методичною похибкою) відображення векторів вхідних сигналів у вектори вихідних, одночасно виділяючи на виходах нейронних елементів прихованого шару сигнали всіх компонентів інформаційного об’єкта. Причому, перша компонента задає напрямок, вздовж якого дисперсія максимальна, наступна компонента проводиться таким чином, що вздовж неї максимізується залишкова варіація і т.д. Достатньо близьким, через виділення головних компонентів, є також режим відображення відгуків на підставі заданих входів (проективна задача), так як існує взаємно однозначна відповідність між координатами точок еліпсоїду розсіювання входів та гіпертіла. На підставі єдиного підходу розв’язуються також задачі ущільнення даних, факторного аналізу, кластеризації в режимі самонавчання, фільтрації сигналів та ін.

Особливості навчання. В автоасоціативному режимі моделей ГП послідовні кроки перетворень гіпертіла реалізуються шляхом проектування його на ортогональні гіперплощини, що проходять через початок координат, починаючи з вимірності n і аж до нульової вимірності. Даний режим забезпечує розв’язок завдань ущільнення даних, факторного аналізу, кластеризації, фільтрації; функції відновлення пропущених табличних даних для даного режиму, включаючи невідомі відгуки, забезпечуються введенням циклічного зворотного зв’язку.

Режим відображення заданих входів у невідомі відгуки виконується шляхом покрокових геометричних перетворень в (n+1)-вимірному просторі реалізацій, де n – число незалежних входів моделі; на першому кроці перетворень визначається найдовша вісь еліпсоїда розсіювання, яка співпадатиме з першою координатою входів на еліпсоїді; апроксимуємо гіперповерхні відгуку (кожну з них окремо) елементарною гіперповерхнею від першої координати входів; отримуємо залишок такої апроксимації, як різницю вихідних координат гіперповерхні і елементарної апроксимуючої гіперповерхні; вимірність задачі скоротилася на одиницю; на другому кроці визначаємо наступну за розміром вісь еліпсоїда (друга координата входів); апроксимуємо залишок від попереднього кроку апроксимації елементарною гіперповерхнею від другої координати входів; число кроків перетворень не перевищує n; результатами навчання є параметри системи координат входів на еліпсоїді та параметри моделей елементарних гіперповерхонь для кожного кроку перетворень.

Функціонування. Як і в попередньому випадку реалізується покроково, де на першому кроці вектор входів перетворюється в першу координату входів на еліпсоїді розсіювання (згідно напрямку найдовшої осі, отриманої при навчанні), для даної координати знаходиться відгук на першій елементарній гіперповерхні далі знаходиться відгук для другої координати входів на еліпсоїді і т.д. Шуканий відгук обчислюється як зважена сума відгуків, отриманих на елементарних поверхнях.

Особливості розв’язку лінійних задач. Гіперповерхні відгуку є гіперплощинами, додатковий вимір моделі повністю визначається шумовими компонентами та похибками заокруглень. Результати застосування ГП – основні виміри гіперплощини співпадають з результатами отриманими за допомогою відомих методів РСА. Однак, застосування ГП надає ряд переваг, зокрема, даний метод швидкий, неітеративний, без накопичення похибок і помітних обмежень на вимірність; відпадає потреба в розв’язках систем нормальних рівнянь, або у здійсненні ітеративної адаптації.

Для гладких нелінійних залежностей ГП забезпечує побудову криволінійної ортогональної системи координат моделі, виділення нелінійних головних компонентів, близьких до незалежних.

В режимі застосування навченої моделі ГП існує принципова можливість аналізу координат (компонентів моделі) на передбачуваність та вилучення шумових компонент.

В найпростішому випадку, вважаючи дані координати незалежними, аналіз виконується шляхом покрокової оцінки змін похибок в режимі застосування і маскування компонентів, що сприяють збільшенню похибок.

В модусі прогнозування часових послідовностей забезпечується об’єктивне виділення та аналіз всіх незалежних трендів, що представляють послідовність, де кількість трендів рівна розміру обраного вхідного часового вікна.

В багатьох задачах еліпсоїд розсіювання виявляється суттєво “сплюснутим” по багатьох напрямках, отже даними координатами входів можна знехтувати. Це зменшує вимоги до необхідного об’єму тренувальною вибірки. Для надмалих тренувальних вибірок, в .т.ч. коли число векторів менше числа первинних входів, можна обмежитися лише декількома “найдовшими” координатами входів на еліпсоїді – основними факторами і отримати можливість здійснювати навчання і генералізацію на основі врахування лише цих факторів. Класичні методи передбачення в подібних випадках не забезпечать отримання жодної корисної інформації.

Особливості розв’язування суттєво нелінійних задач. Застосовується режим, що забезпечує перетворення первинних входів у радіальні базові функції. Відбувається лінеаризація задачі, однак відомі варіанти RBF та гібридних мереж мають суттєві недоліки: погана генералізація, відсутність екстраполяційних властивостей, потреба у великих тренувальних вибірках.

Застосування RBF методу на основі ГП, включаючи детерміновану повторюваність розташування центрів RBF на основі виділених головних компонентів, повністю знімає перелічені недоліки. Це стає можливим за рахунок відкидання малозначимих та шумових компонентів, селекції необхідних компонентів відповідно до тренувальної та тестової вибірок. В результаті забезпечується поєднання властивості відтворювати складні нелінійні залежності та здатність до генералізації в умовах існуючих вибірок даних; додатково створюються умови для візуалізації даних в координатах обраних компонентів.

Лекція № 19. Основи нечіткої логіки.

Нечітка логіка презентує специфічний розділ м’яких обчислень, до якого також відносять штучні нейромережі, генетичні алгоритми, імовірнісні (байесівські методи). Вважається, що м’які обчислення ефективні для задач моделювання складних систем, або керування складними системами в умовах невизначеності.

Етапи розвитку нечіткої логіки.

Поштовх до появи нечіткої логіки пов’язують зі створенням квантової теорії, в основі якої є принцип невизначеності. За відкриття принципу невизначеності у 1932 році Гейзенбергу присудили Нобелівську премію. Принцип невизначеності привів до появи багатозначної логіки. Межами невизначеності є:

• TRUE;

• FALSE.

Таким чином у граничному випадку нечітка логіка зводиться до булевої алгебри.

І етап. Англійський вчений М. Блек першим ввів поняття неперервної логіки, яку застосував до множин елементів і символів.

ІІ етап. Цей етап безпосередньо пов'язаний з Лотфі Заде, якого вважають творцем нечіткої логіки. У 1965 р. ним опублікувана фундаментальна праця «Нечіткі множини», де викладено низку важливих принципів. Принцип несумісності – чим складніша система, тим менша здатність давати точні і одночасно практичні судження про її поведінку, тобто після деякого порогу точність і практичний зміст взаємовиключаються.