Двоскерована асоціативна пам’ять

Ця мережна модель була розроблена Бартом Козко (Bart Kosko) і розширює модель Гопфілда. Множина парних образів навчається за образами, що представлені як біполярні вектори. Подібно до мережі Гопфілда, коли представляється зашумлена версія одного образу, визначається найближчий зразок, асоційований з ним.

На рис. 10.3 показаний приклад двоскерованої асоціативної пам'яті. Вона має стільки входів, скільки є вихідних нейронів. Два приховані прошарки містяться на двох окремих асоціативних елементах пам'яті і представляють подвоєний розмір вхідних векторів. Середні прошарки повністю з'єднуються один з одним. Вхідний та вихідний прошарки потрібні для реалізації засобів введення та відновлення інформації з мережі.

Середні прошарки розроблені для збереження асоційованих пар векторів. Коли зашумлений вектор образу вважається вхідним, середні прошарки коливаються до досягнення стабільного стану рівноваги, який відповідає найближчій навченій асоціації і буде генерувати початковий навчальний зразок на виході. Подібно до мережі Гопфілда, двоскерована асоціативна пам'ять є схильною до неправильного відшукування навченого образу, якщо надходить невідомий вхідний вектор, який не був у складі навчальної множини.

Двоскерована асоціативна пам'ять відноситься до гетероасоціативної пам'яті. Вхідний вектор надходить на один набір нейронів, а відповідний вихідний вектор продукується на іншому наборі нейронів. Вхідні образи асоціюються з вихідними. Для порівняння: мережа Гопфілда є автоасоціативною. Вхідний зразок може бути відновлений чи виправлений мережею, але не може бути асоційований з іншим зразком. У мережі Гопфілда використовується одношарова структура асоціативної пам'яті, у якій вихідний вектор з'являється на виході тих же нейронів, на які надходить вхідний вектор.

Двоскерована асоціативна пам'ять, як і мережа Гопфілда, здатна до узагальнення, виробляючи правильні вихідні сигнали, незважаючи на спотворені входи.

Розглянемо схему двоскерованої асоціативної пам'яті. Вхідний вектор A обробляється матрицею ваг W мережі, у результаті чого продукується вектор вихідних сигналів мережі B. Вектор B обробляється транспонованою матрицею WT ваг мережі, яка продукує сигнали, що представляють новий вхідний вектор A. Цей процес повторюється доти, поки мережа не досягне стабільного стану, у якому ні вектор A, ні вектор B не змінюються. Для порівняння: мережа Гопфілда є автоасоціативною. Вхідний зразок може бути відновлений чи виправлений мережею, але не може бути асоційований з іншим зразком. У мережі Гопфілда використовується одношарова структура асоціативної пам'яті, у якій вихідний вектор з'являється на виході тих же нейронів, на які надходить вхідний вектор.

Двоскерована асоціативна пам'ять, як і мережа Гопфілда, здатна до узагальнення, виробляючи правильні вихідні сигнали, незважаючи на спотворені входи.

Розглянемо схему двоскерованої асоціативної пам'яті. Вхідний вектор A обробляється матрицею ваг W мережі, у результаті чого продукується вектор вихідних сигналів мережі B. Вектор B обробляється транспонованою матрицею WT ваг мережі, яка продукує сигнали, що представляють новий вхідний вектор A. Цей процес повторюється доти, поки мережа не досягне стабільного стану, у якому ні вектор A, ні вектор B не змінюються.

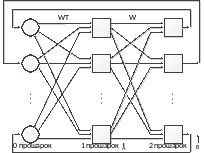
Рис. 16.3. Двоскерована асоціативна пам'ять

Нейрони в прошарках 1 і 2 функціонують, як і в інших парадигмах, обчислюючи суму зважених входів і значення передатної функції F:

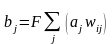
або у векторній формі:

B=F(AW)

де B - вектор вихідних сигналів нейронів прошарку 2, A - вектор вихідних сигналів нейронів прошарку 1, W - матриця ваг зв'язків між прошарками 1 і 2, F - передатна функція.

Аналогічно A=F(BWT), де WT є транспонованою матрицею W.

В якості передатної функції використовується експонент та сигмоїда.

Прошарок 0 не робить обчислень і не має пам'яті. Він є лише засобом розподілу вихідних сигналів прошарку 2 до елементів матриці WT.

Формула для обчислення значень синаптичних ваг:

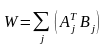
де A_j і B_j - вхідні і вихідні сигнали навчальної вибірки.

Вагова матриця обчислюється як сума добутків всіх векторних пар навчальної вибірки.

Системи зі зворотним зв'язком мають тенденцію до коливань. Вони можуть переходити від стану до стану, ніколи не досягаючи стабільності. Доведено, що двоскерована асоціативна пам'ять безумовно стабільна при будь-яких значеннях ваг мережі.

Області застосування. Асоціативна пам'ять, розпізнавання зразків.

Недоліки. Ємність двоскерованої асоціативної пам'яті жорстко обмежена. Якщо n - кількість нейронів у вхідному прошарку, то кількість векторів, що можуть бути запам'ятовані в мережі не перевищує L=n/2log2n. Так, якщо n=1024, то мережа здатна запам'ятати не більш 25 зразків.

Двоскерована асоціативна пам'ять має деяку непередбачуваність у процесі функціонування, можливі помилкові відповіді.

Переваги.

У порівнянні з автоасоціативною пам'яттю (наприклад, мережею Гопфілда), двоскерована асоціативна пам'ять дає можливість будувати асоціації між векторами A і B, що у загальному випадку мають різні розмірності. За рахунок таких можливостей гетероасоціативна пам'ять має більш широкий клас застосувань, ніж автоасоціативна пам'ять.

Двоскерована асоціативна пам'ять - проста мережа, що може бути реалізована у виді окремої НВІС чи оптоелектронним способом.

Процес формування синаптичних ваг простий і швидкий. Мережа швидко збігається в процесі функціонування.

Модифікації.

Сигнали в мережі можуть бути як дискретними, так і аналоговими. Для обох випадків доведена стабільність мережі. Були запропоновані моделі двоскерованої асоціативної пам'яті з навчанням без вчителя (адаптивна двоскерована асоціативна пам'ять). Введення латеральних зв'язків всередині прошарку дає можливість реалізувати конкуруючу двоскеровану асоціативну пам'ять.

Контрольні запитання

1. Основні відмінності топологій БШП та ШНМ Гопфілда.

2. Особливості навчання ШНМ Гопфілда в порівнянні з навчанням БШП.

3. Області застосування ШНМ Гопфілда.

4. Фізичні аналогії для ШНМ Гопфіода.

5. Обмеження ШНМ Гопфілда.

6. Відмінності двоскерованої асоціативної пам’яті від ШНМ Гопфілда.

7. Призначення двоскерованої асоціативної пам’яті.

Лекція № 17. ШНМ з нейронними елементами радіального типу.

Мережа з радіальними базовими функціями в найбільш простій формі – це мережа з трьома шарами: звичайним вхідним шаром, який виконує розподілення даних зразка для першого прошарку ваг, прихованим і вихідним прошарками. Відображення від вхідного прошарку до схованого прошарку є нелінійним, а відображення прихованого прошарку у вихідний - лінійне. Звичайно (але не завжди) кількість прихованих елементів більше кількості вхідних елементів. Ідея полягає у тому, що якщо нелінійну проблему розмістити в просторі збільшеної розмірності деяким нелінійним чином, то імовірність того, що вона буде лінійно розділимою, виявляється вищою.

Розглянемо відображення першого прошарку. З кожним прихованим елементом пов'язується деяка функція . Кожна з цих функцій має комбінований вхід і породжує значення активності, що подається на вихід. Сукупність значень активності всіх прихованих елементів визначає вектор, на який відображається вхідний вектор:

,

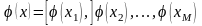де М позначена кількість прихованих елементів, а х — вхідний вектор.

Зв'язки елемента прихованого прошарку визначають центр радіальної функції для даного прихованого елемента. Вхід для кожного елемента вибирається рівним евклідовій нормі:

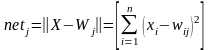
де n позначено кількість вхідних елементів.

Для прихованих елементів використовують самі найрізноманітніші функції активації, наприклад, функцію Гауса 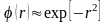або функцію 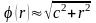. Нейронний елемент Гаусівського типу показаний на рис. 17.1.

Рис. 17.1. Нейронний елемент гаусівського типу

Оператор R здійснює обчислення евклідової віддалі до центру RBF – опорної точки, яка відповідає даному нейронному елементу, f – обчислення Гаусівської функції

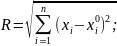
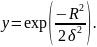
Форма гасівської функції активації показана на рис. 11.2. Чим більша величина δ, тим функція пологіша.

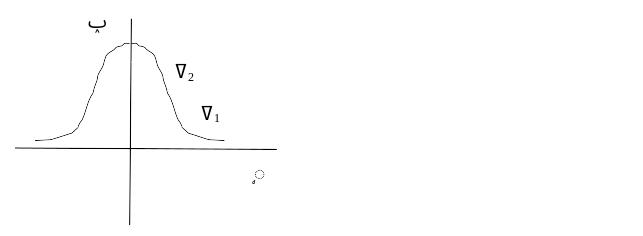
Рис. 11.2. Гаусівська функція активації

У випадку якщо вхідні вектори пронормовані до одиничного радіусу

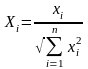, то оператор R набуває вигляду

і буде відрізнятись від класичного формального нейрона лише гаусівською функцією активації.

Структура нейромереж радіальних базових функцій

Входами нейромережі RBF є x_1, x_2, x₃. Наступним є шар нейронних елементів з гаусівськими функціями активації, кожен з нейронів відповідає центру радіальної функції. Кожен центр визначається своїми координатами (x₁^і_, x₂^і_{, …} x₃^і) у випадку, якщо вхідний вектор співпадає з координатам центру, то на виході нейронного елемента маємо сигнал 1.

Вихідним каскадом нейромережі може бути може бути також інша нейромережа, зокрема одношаровий перцептрон.

Питання, які необхідно вирішувати для налагодження і навчання нейромережі RBF.

1. Вибір центрів радіальних функцій, як правило число центрів більше n.

m>n

Найпростіше центри представляють собою випадкову вибірку з векторів тренувальних даних. В якості центрів обираються центри кластерів вхідних даних. Для кластеризації можна застосувати будь-який відомий алгоритм кластеризації, в тому числі само організаційну карту особливостей карт Коганена, як перший каскад .

2. Вибір 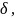яка є параметром розмаху гаусівської функції

Найпростіший варіант – вибирати спільне 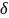для всіх центрів RBF. При нерівномірному представленні даних такий вибір не забезпечує необхідну точність. Для підвищення точності застосовують метод k «наближчих сусідів» - KNN, Метод передбачає для кожної точки вибірки даних обчислення віддалей до k найближчих точок. обирається пропорційною до середньої віддалі до цих точок.