Дифференциальные уравнения второго порядка.

• Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами  .

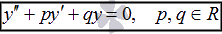ЛОДУ с постоянными коэффициентами является очень распространенным видом дифференциальных уравнений. Их решение не представляет особой сложности. Сначала отыскиваются корни характеристического уравнения  . При различных p и q возможны три случая: корни характеристического уравнения могут быть действительными и различающимися  , действительными и совпадающими   или комплексно сопряженными  . В зависимости от значений корней характеристического уравнения, записывается общее решение дифференциального уравнения как  , или  , или   соответственно.

Для примера рассмотрим линейное однородное дифференциальное уравнение второго порядка с постоянными коэффициентами  . Корнями его характеристического уравнения   являются k ₁ = -3 и k ₂ = 0. Корни действительные и различные, следовательно, общее решение ЛОДУ с постоянными коэффициентами имеет вид

Подробное описание теории и разобранные решения примеров и задач смотрите в разделе линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами.

• Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами  .

Общее решение ЛНДУ второго порядка с постоянными коэффициентами y ищется в виде суммы   общего решения соответствующего ЛОДУ   и частного решения   исходного неоднородного уравнения, то есть,  . Нахождению общего решения однородного дифференциального уравнения с постоянными коэффициентами  , посвящен предыдущий пункт. А частное решение   определяется либо методом неопределенных коэффициентов при определенном виде функции f(x), стоящей в правой части исходного уравнения, либо методом вариации произвольных постоянных.

В качестве примеров ЛНДУ второго порядка с постоянными коэффициентами приведем

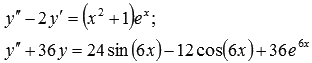
Разобраться в теории и ознакомиться с подробными решениями примеров мы Вам предлагаем на странице линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами.

• Линейные однородные дифференциальные уравнения (ЛОДУ) 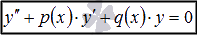  и линейные неоднородные дифференциальные уравнения (ЛНДУ) второго порядка  .

Частным случаем дифференциальных уравнений этого вида являются ЛОДУ и ЛНДУ с постоянными коэффициентами.

Общее решение ЛОДУ   на некотором отрезке [a; b]представляется линейной комбинацией двух линейно независимых частных решений y ₁ и y ₂ этого уравнения, то есть,  .

Главная сложность заключается именно в нахождении линейно независимых частных решений дифференциального уравнения этого типа. Обычно, частные решения выбираются из следующих систем линейно независимых функций:

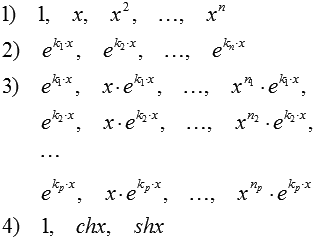
Однако, далеко не всегда частные решения представляются в таком виде.

Примером ЛОДУ является  .

Общее решение ЛНДУ   ищется в виде  , где   - общее решение соответствующего ЛОДУ, а   - частное решение исходного дифференциального уравнения. О нахождении   мы только что говорили, а   можно определить, пользуясь методом вариации произвольных постоянных.

В качестве примера ЛНДУ можно привести  .

Теорию и решение примеров смотрите в разделе линейные дифференциальные уравнения второго порядка.

К началу страницы